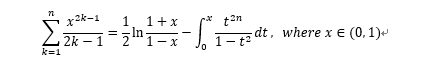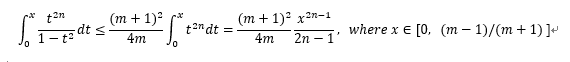有理数の自然対数を任意の精度以上の精度で有理数によって近似する

やり尽くされたようなテーマですが、
高校数学3までの知識があれば理解及び実装が容易のため、投稿させて頂きます。

入力: 非負有理数 m(!=1) & 精度p (P＞0)
目標: |ln(m)-A|<p　となるような有理数Aを求める。(ln(x)でxの自然対数を表す。)
方法:

次の2つの命題が証明されます。ただし、m＞1
(i)

(ii)

(i)はnに関する帰納法、
(ii)は0<=t<=x<=(m-1)/(m+1)という不等式を用いればよいです。

(i), (ii)から、

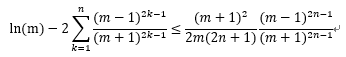
が得られるので、(右辺)＜pを満たすnを求めて、左辺の第2項を計算し、それが近似値として使えます。
m＜1の場合は、㏑(1/m)の近似値を求めて -㏑(1/m)を出力します。

以下、Pythonコード

Python

import numpy as np

n=0.03 #input
m=n if n>=1 else 1/n 
# print(m)
p=0.0001 #input


def error(m,n):
    denom=2*m*(2*n+1)*(m+1)**(2*n-1)    
    return ((m+1)**2)*((m-1)**(2*n-1))/denom

def ap_A(n,m):
    s=0
    for k in range(1,n+1):
       r=((m-1)/(m+1))**(2*k-1)
       s+=r/(2*k-1)
       #print(s)
    return 2*s

def n_finder(m,p):
    n=1
    while error(m,n)>p:
        n+=1
        #print(n,error(m,n))
    return n

ap=ap_A(n_finder(m,p),m)
if n<1: ap=-ap
print("An approximate value A s.t. |ln(n)-A|<p is ", ap) # output of result
print(abs(np.log(n)-ap)<p) # check