先日投稿したDbDに関する記事は何も考えずに可視化しただけなので，もうすこしちゃんと分析できないものかと思って大学で習った内容を復習しつつ勉強してきました．今回はそのまとめです．
グラフとは
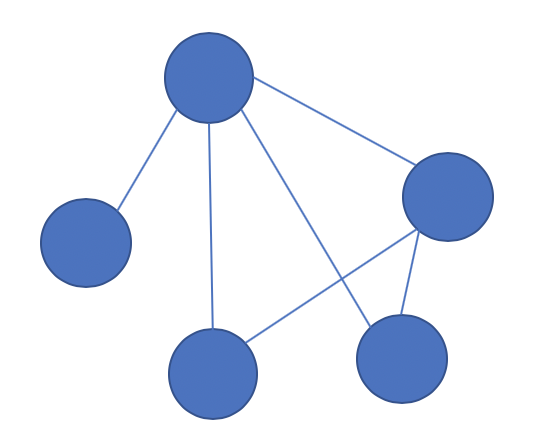
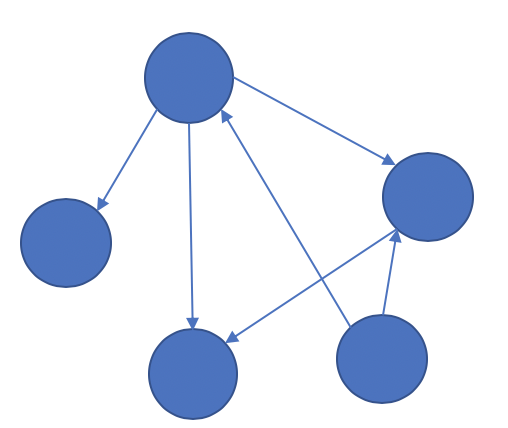
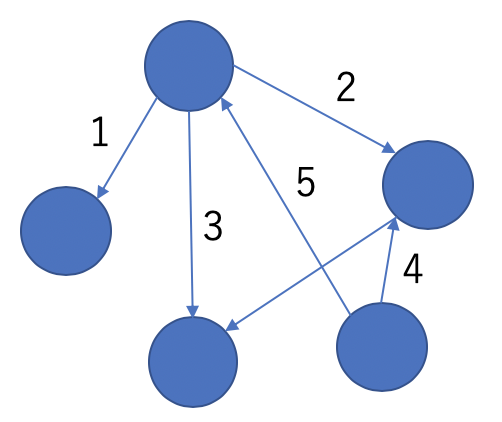
複数の要素の関係性を表現するためのデータ構造をグラフと呼ぶ．グラフはエッジとノードの集合で記述される．エッジには方向を持つものや重みを持つものも存在し，例えばノード間の距離等の移動コストなどが重みとして付加される．
無向グラフ
有向グラフ
重み付き有向グラフ
ケーニッヒスベルクの橋
グラフ理論の起源となる問題「7つの橋をそれぞれ一回だけ渡って全ての橋を渡ることができるかどうか（一筆書き）」
グラフ理論の祖（ポケモンで言うとアルセウス，モンハンで言うとミラルーツ）レオンハルト・オイラーは不可能であると結論付ける．
グラフモデル
現代の社会に転がっているようなデータ（ソーシャルデータ）の多くは，グラフで記述することが可能である．実世界をグラフでモデル化し，構造を把握しようという目的から多くのグラフモデルが提案されている．
ソーシャルデータの例
- Webページ
- 道路交通ネットワーク
- 購買履歴
など
ERモデル
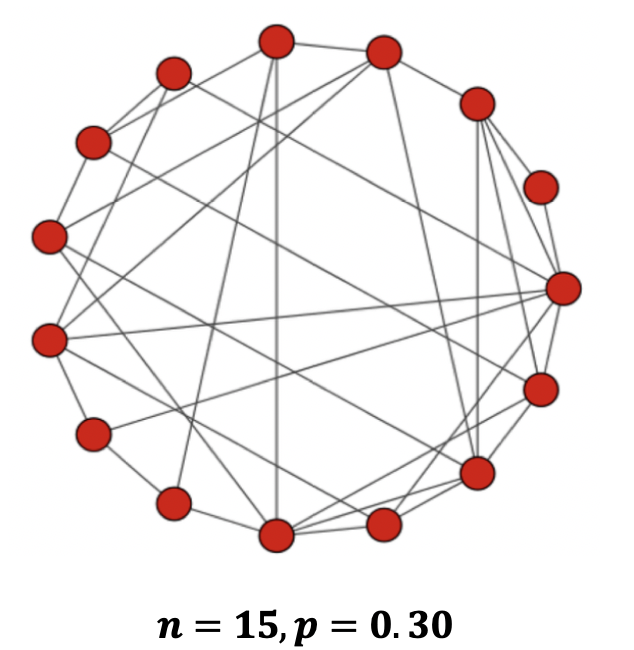
ランダムなネットワークモデル
特徴
- 最もシンプルなモデル
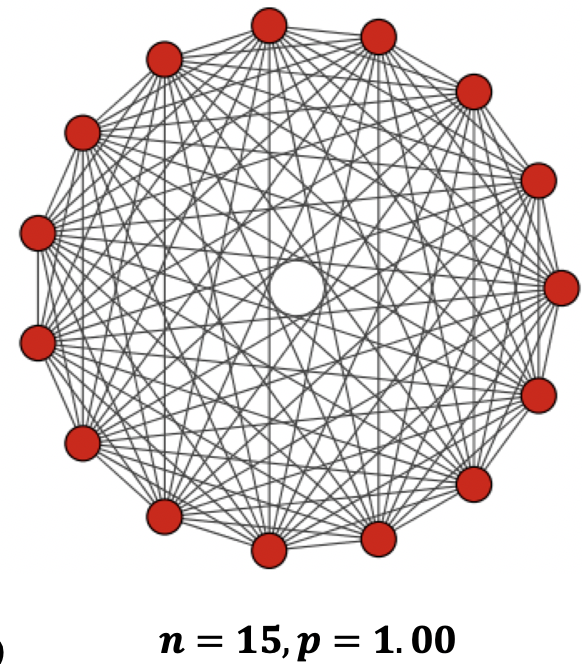
- 全ノード間に一定確率pでエッジを張る
- ランダム性を持つグラフ
- エッジ生成確率を1.00にすると完全グラフ（全ノード間にエッジ）になる
ERモデル
完全グラフ
必要なパラメータ
- ノード数n, エッジ生成確率p
アルゴリズム
- ノードをn個作る
- ノードペア$_nC_2$（n個から2個を抽出する組み合わせ）の中から一つ選択し，確率pでエッジを張る
- 2の処理を全てのノードペアに対して行う
ランダム性を持たせて生成するという最も単純な考えの元作られたモデル．でも，現実にあるデータってこんなランダム性はもっていないので実用性が低い．
ソーシャルネットワークが持つ性質
ERモデルでソーシャルネットワークのモデル化が困難である理由は，ソーシャルネットワークが持つ以下の三つの理由からくる．
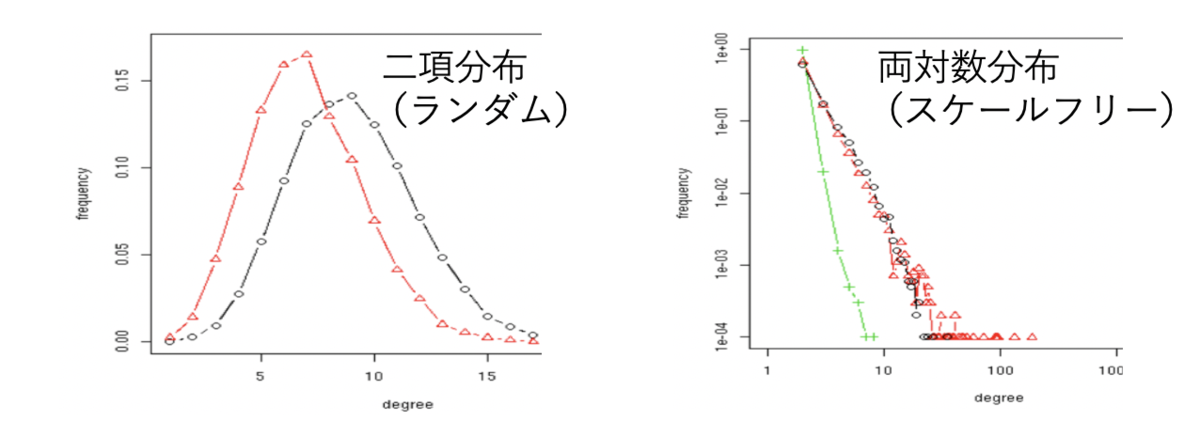
- スケールフリー性: 次数の分布が極端に異なる
- クラスタ性: 三部クリークを含む比率が高い
- スモールワールド性: 平均最短経路長が短い
グラフモデルを評価・検討する上で，ランダムなERモデルと比較して上記の三つの性質が現れるかどうかを評価する必要がある．
BAモデル
スケールフリー性を持つようなグラフモデル．
特徴
- 次数分布が冪乗則に従う
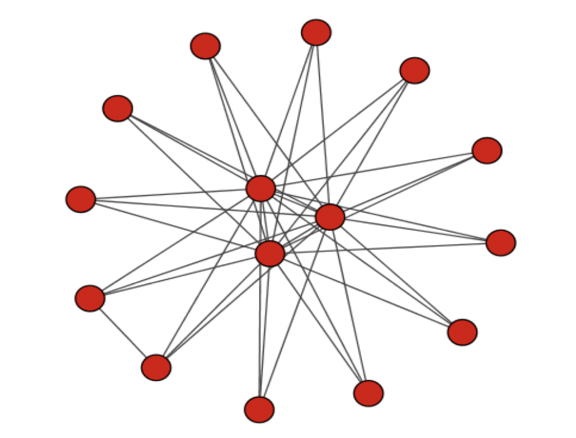
- 中心にいる人気者は少数派であり，多くは狭い友好関係の中で生きている(悲しい）
BAモデル
次数分布
必要なパラメータ
- ノード数𝒏,初期ノード数$n_0$,平均次数𝒌(𝒌≤$n_0$≪𝒏)
アルゴリズム
- $n_0$個のノードからなる完全グラフを作る
- 新しいノード$𝒗$を１つ追加する
- 既に存在しているノードから，優先選択確率$𝒑(𝒖)$に従って$k$ノードを選択し，ノード$𝒗$からエッジを張る
- 2 ~ 3をノード数が$n$になるまで繰り返す．
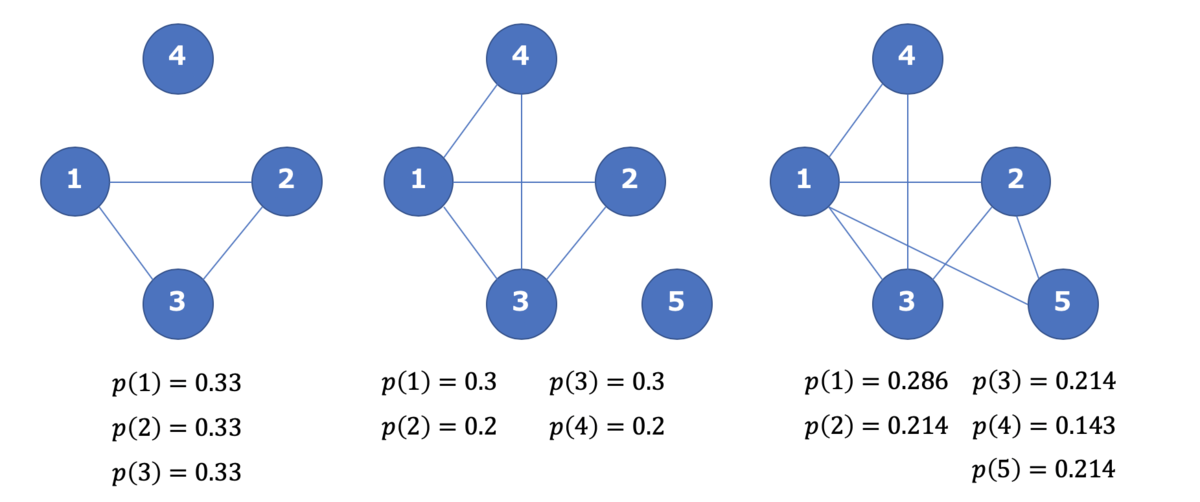
ここでは，優先選択確率というものを導入している．
$p(u) = \frac {d_u} {\sum_{u \in V} d_u}$
この式は，「既に友達がたくさんいる人には友達がさらに増える友達がいない人には今後も友達が出来ない」というマタイ効果のようなものを再現している．
BAモデルの生成過程
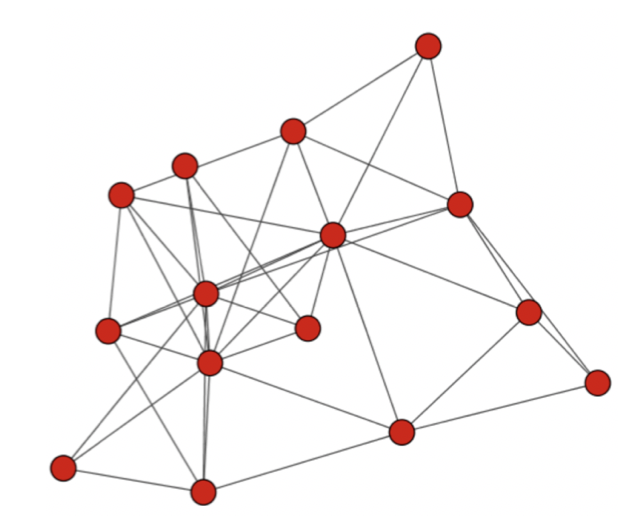
生成したモデルを見ても，中心となるようなノードが3つほど出てきたのがわかる．
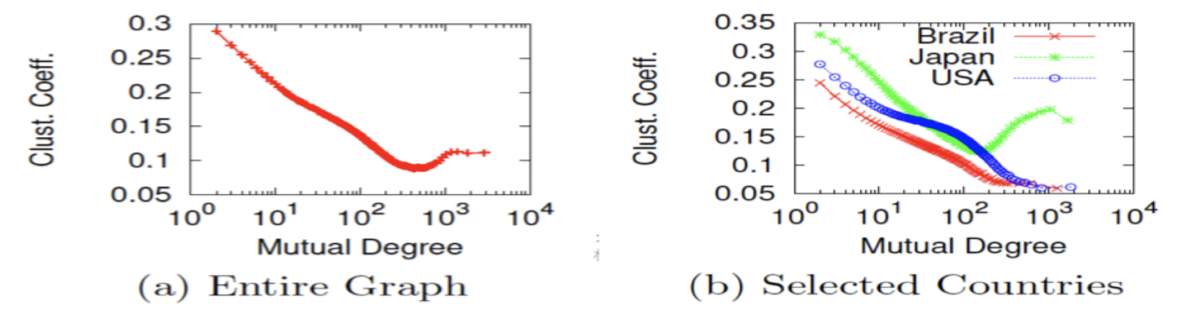
スケールフリー性に関しては，日本人のTwitterの特異性に触れた面白い論文がある．
Information Network or Social Network? The Structure of the Twitter Follow Graph,” In Proc. WWW 2014.
この論文では，Twitterは日本人ユーザのせいでソーシャルネットワークの要件を満たせない可能性があることを示唆している．
日本には相互フォロワー1000人くらいの人たちの集団，いわゆるクラスタがたくさんあるせいで，Twitter全体の分布に影響を与えてしまっているらしく，分布の冪乗則を脅かしているらしい．集団で集まるのが大好きな国民性があるのかも．
相互フォロワー分布
HKモデル
クラスタ性を持つグラフモデル.
特徴
- 三部クリーク（三角形）を多く含む
- 友達の友達が自分の友達である割合が高い
- BAモデルの改良版
友達の友達が自分の友達（三部クリーク）
HKモデル（三角っぽく）
HKモデル（円状）
HKモデルはBAモデルの改良版であるため，スケールフリー性も確保している．アルゴリズムを見ればより理解しやすい．
必要なパラメータ
- ノード数$𝒏$，初期ノード数$𝒏_𝟎$，平均次数$𝒌$，確率$𝜷$
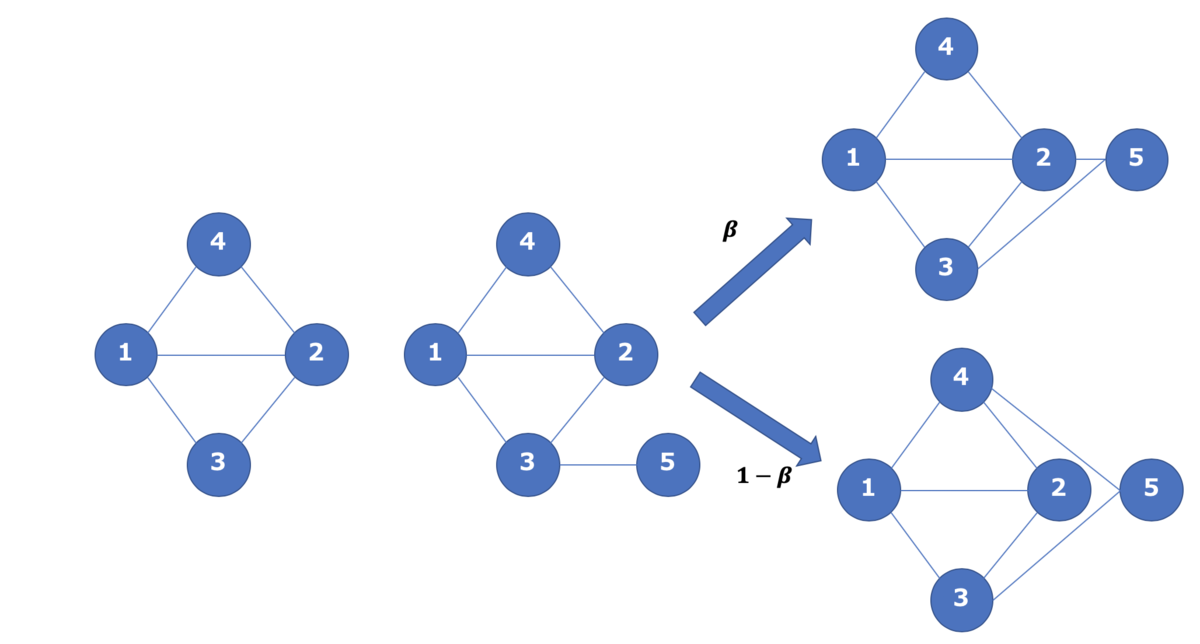
アルゴリズム
- $n_𝟎$個のノードからなる完全グラフを作る
- 新しいノード$𝒗$を一つ追加する
- 以下の処理に従いノード$𝒗$から$𝒌$本のエッジを張る
-- 優先選択確率$𝒑(𝒖)$に従いノード$𝒗^′$を選択しエッジを張る
-- 残りの$𝒌−𝟏$本は以下に従いエッジを張る
--- 確率$𝜷$で，ノード$𝒗^′$の$𝒗$を除く隣接ノードからランダムにノードを選択しエッジを張る（クラスタ性確保！）
--- 確率𝟏−𝜷で，優先選択確率𝒑(𝒖)に従ってノード𝒗^′以外のノードを選択しエッジを張る（スケールフリー性確保！） - 2 ~ 3をノード数が$n$になるまで繰り返す
HKモデルの生成過程
確率$β$はクラスタ性を確保するのか，スケールフリー性を確保するのかを選択させる確率．
WSモデル
スモールワールド性を持つグラフモデル
特徴:
- 平均最短経路長が短い
- 任意のノードペア間の距離が短い
- わあ！世界は狭いね!という感じがある
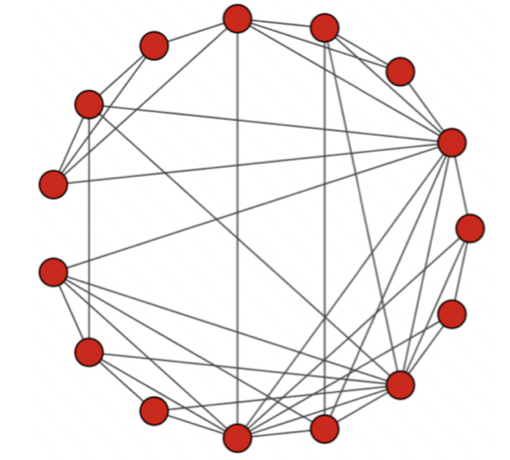
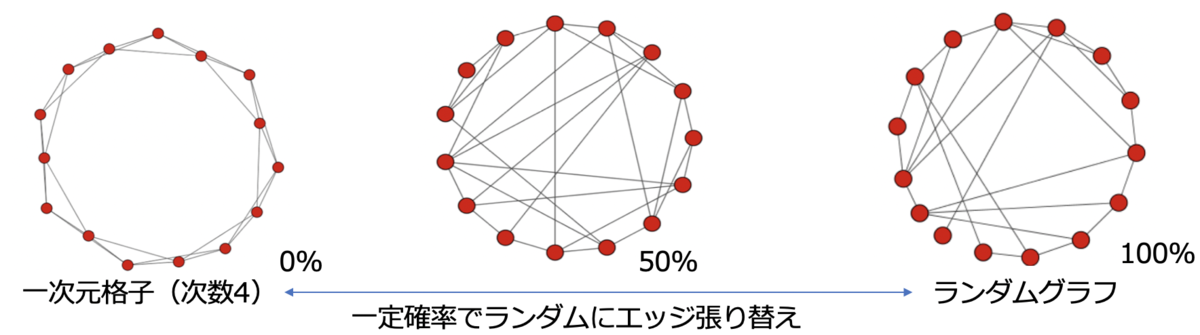
生成アルゴリズムは簡単で，一次元格子を作成してランダムにエッジを張り替えるだけ．
WSモデルの生成過程
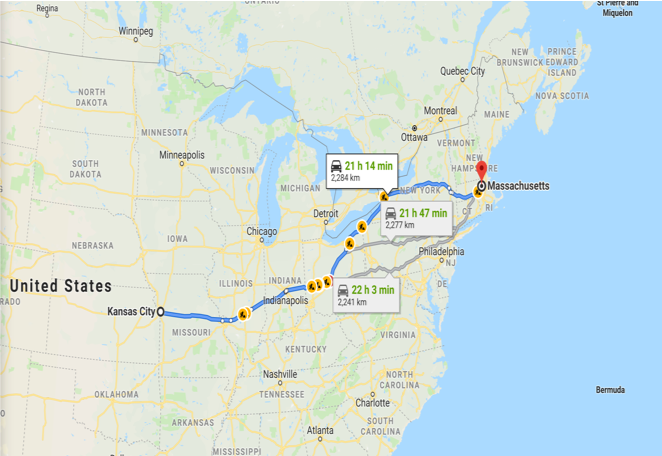
スモールワールド性に関して，ミルグラムの実験（1967）が有名．
カンザス州の住人に手紙を預け，2200km先のマサチューセッツ州に住む特定の人物に手紙を届けるように指示．
ルールは以下の一つだけ
- "手紙の伝達手段は個人的な知り合いへの手渡しのみ"
カンザス－マサチューセッツ間
結果は，平均仲介人数が6人．これを6次の隔たりといい，6人辿ればだいたいの人間にアクセスできることを示唆した．
つまり，スモールワールド性とは情報の伝達速度が早いことを示すとも言える．
最近の調査だと，
- mixi（2008）: mixi上で6人辿れば95%へアクセスできる
- FaceBook（2016）: FaceBook上の16億人分のソーシャルネットワークを分析し，全世界では4.57人，米国内では3.5人で全体にアクセス
などがある．
まとめ
ソーシャルデータをモデル化するグラフモデルをまとめました．
- ERモデル: ランダム性のあるモデル, ソーシャルデータには適さないことから比較に用いられる
- BAモデル: スケールフリー性を持つモデル
- HKモデル: BAモデルを改良，クラスタ性を持つモデル
- WSモデル: スモールワールド性を持つモデル
このへんのモデルを参考にして今度は身近なデータをグラフで表してみたいと思っています！
また今回グラフの描画にはCytoscapeを使わせていただきました．
参考文献
- 増田直紀、今野紀雄, “複雑ネット ワーク 基礎から応用まで”近代科学社.
- Erdős, P.; Rényi, A. "On Random Graphs Ⅰ". Publicationes Mathematicae. 1959, p.290-297.
- Albert, Réka; Barabási, Albert-László (2002). "Statistical mechanics of complex networks". Reviews of Modern Physics. , p.47–97.
- S. A. Myers et al., ”Information Network or Social Network? The Structure of the Twitter Follow Graph,” In Proc. WWW 2014.
- Holme,P.; Kim,B.J. "Growing Scale-Free Networks with Tunable Clustering". Phys. Rev. E 65, 026107 . Phys. Rev. E, 2001, p.440-442.
- Watts,D.; Strogatz,S.H. "Collective dynamics of ‘small-world’ networks". Publicationes Mathematicae. . Nature(332), 1998, p.440-442.
- Stanley Milgram, "The Small World Problem", Psychology Today, May 1967. pp 60 - 67.