はじめに
友人たちと簡単な強化学習を使ったプロジェクトに取り組んだので、その記録もかねて記事にまとめてみた。
背景
混雑した市街地において駐車場探しに悩まされた経験のある方は多いだろう。一説によると市街地における交通量の約30%は駐車場探しのための徘徊らしい1。
道路状況(状態)を考慮して、各車両の駐車場選択をリアルタイムで指示(行動選択)できれば、道路の混雑緩和を達成できるのではないかと考えた。
そこで、リアルタイムで駐車場への入庫を指示する誘導灯を導入し、Deep Q-Networkを用いてそれらを学習させた。
アイデア
既往研究
強化学習を用いた信号制御の研究としては
Pol and Oliehoek(2016), Coordinated Deep Reinforcement Learners for Traffic Light Control, NIPS'16 Workshop on Learning, Inference and Control of Multi-Agent Systems
などが挙げられる。
この研究では2次元道路ネットワーク上でDQNを用いて信号制御を学習しているわけだが、報酬関数の設計がミソで、渋滞や車両の待ち時間、急停止の有無などをうまく報酬関数に組み込んでいる。
参考:既往研究で用いられた報酬関数
$ r_t = -0.1c - 0.1 \sum_{i=1}^N j_i - 0.2 \sum_{i=1}^N e_i - 0.3 \sum_{i=1}^N d_i - 0.3\sum_{i=1}^N w_i$
$i = 1, \dots, N$:エージェント(車両)
$r$:報酬
$c$:信号が変わったか否か
$j$:車両が渋滞に巻き込まれたか否か
$e$:車両が急停止したか否か
$d$:車両のスピードが一定の速度(制限速度)以下か否か
$w$:車両が赤信号で停止したか否か
しかし、この研究では車両が単純に道路を通過するだけで、渋滞の一因である駐車とそれに伴う一時停止などは扱えていない。さらに、交通シミュレーションにSUMO2というシミュレータを使っており、少々扱いが面倒。
このプロジェクトのアイデア
そこで本プロジェクトでは
- 車両の駐車行動に対象を絞り、駐車場の誘導灯を学習
- 道路ネットワークおよび駐車・渋滞の表現にセルオートマトンを導入し、より扱いやすく
- 渋滞を低減しながら駐車時間を短くするよう、各誘導灯を動的に制御
を念頭に実装をおこなった。
モデル
Environment
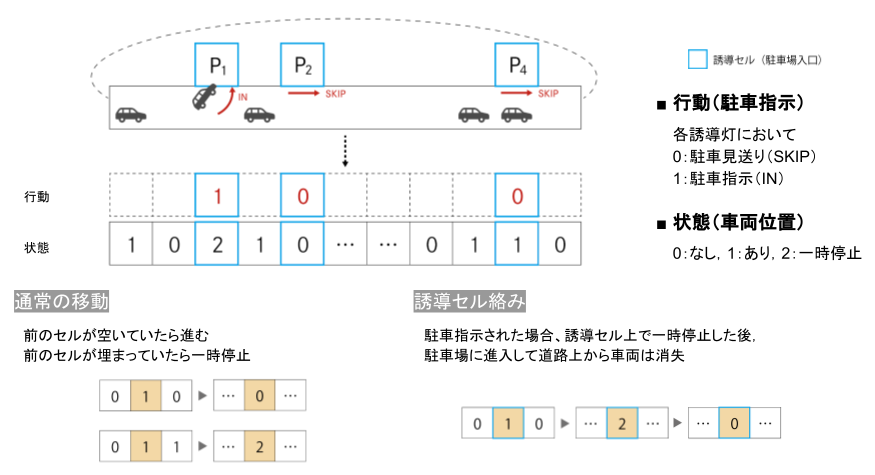
1次元の簡単な道路空間を想定し、セルオートマトンを用いて環境を表現した。
状況設定は上の図の通り。
t=0時点において1次元道路空間上に車が初期位置に並ぶ。道路空間沿いにはいくつかの駐車場が設けられており、すべての車はいずれかに入庫したいと考えている。車は道路空間上を進みながら、いずれかの駐車場に入庫する。ここで全ての車にとって駐車場は無差別、つまりどの車もどこの駐車場でもいいから入庫したいと考えている。各車両は駐車場前に設置された誘導灯の指示(IN / SKIP)に従い入庫or見送り。
セル上の状態は
0:車なし
1:車(走行中)あり
2:車(一時停止中)
誘導灯の行動は
0:入庫見送り(SKIP)
1:入庫指示(IN)
遷移規則は
通常移動:前のセルが空いていたら進む。前のセルに車がいたら一時停止。
誘導セル:入庫指示された場合、そのセルで一時停止した後、駐車場に進入して道路上から消失。
以上を踏まえたPythonのコードは以下の通り3。
import os
import numpy as np
import random
class Parking:
def __init__(self, test = False):
self.name = os.path.splitext(os.path.basename(__file__))[0]
self.n_cells = 50 # number of cells
self.n_cars = 20 # number of cars at t=0
self.n_parking = 4 # number of parking
self.enable_actions = ([0, 0, 0, 0], [0, 0, 0, 1], [0, 0, 1, 0], [0, 0, 1, 1],
[0, 1, 0, 0], [0, 1, 0, 1], [0, 1, 1, 0], [0, 1, 1, 1],
[1, 0, 0, 0], [1, 0, 0, 1], [1, 0, 1, 0], [1, 0, 1, 1],
[1, 1, 0, 0], [1, 1, 0, 1], [1, 1, 1, 0], [1, 1, 1, 1])
self.pre_action = [0, 0, 0, 0]
self.parking_position = [10, 20, 30, 40] # fixed parking locations
self.frame_rate = 5
self.rules = [ "000222000000222000000222000", # 111
"000222000000222000000222000", # 110
"220220000220220000220220000", # 101
"220220000220220000220220000", # 100
"000222111000222111000222000", # 011
"000222111000222111000222000", # 010
"220220111220220111220220000", # 001
"220220111220220111220220000" # 000
]
self.frame_rate = 5
self.test = test
# variables
self.reset()
def update(self, action):
# update navigation
for i, p in enumerate(self.parking_position):
self.navigation[p] = action[i]
# update car position
self.car_cells = self.cellautomaton(self.car_cells, self.navigation)
# calculate reward
self.reward = 0
self.terminal = False
self.n_remain = self.count_remain(self.car_cells)
self.n_stop = self.count_stop(self.car_cells)
c = np.sum(np.abs(np.array(action) - np.array(self.pre_action))) / self.n_parking
# reward function
self.reward = - self.n_remain/self.n_init - self.n_stop/self.n_init
if self.n_remain == 0:
self.terminal = True
self.pre_action = action
def rule_choice(self, l, x, r):
# decide the transition rule by the parking navigation
bin_num = int(str(l)+str(x)+str(r), 2)
return self.rules[-(bin_num+1)]
def transition(self, l, x, r, rule):
# decide the next state
tri_num = int(str(l)+str(x)+str(r), 3)
return int(rule[-(tri_num+1)])
def count_remain(self, state):
#count remaining cars
return len([i for i in state if i > 0])
def count_stop(self, state):
# count stopping cars
return len([i for i in state if i == 2])
def cellautomaton(self, state, navigation):
state_new = []
# add 1 cell at the edge for periodic boundary conditions
state = [state[-1]] + state
state.append(state[1])
navigation = [navigation[-1]] + navigation
navigation.append(navigation[1])
# calculate the next state of each cell
for i in range(1, len(state)-1):
rule = self.rule_choice(navigation[i-1], navigation[i], navigation[i+1])
state_new.append(self.transition(state[i-1], state[i], state[i+1], rule))
# delate added edge cells
del navigation[-1]
del navigation[0]
return state_new
def draw(self):
# reset screen
self.screen = np.array(self.car_cells)
def observe(self):
self.draw()
return self.screen, self.reward, self.terminal, self.n_remain, self.n_stop
def execute_action(self, action):
self.update(action)
def reset(self):
random.seed(300) # car position at t=0 is fixed
self.car_cells = [1] * self.n_cars + [0] * (self.n_cells - self.n_cars)
random.shuffle(self.car_cells)
self.n_init = len([i for i in self.car_cells if i > 0])
self.n_remain = self.count_remain(self.car_cells)
self.n_stop = self.count_stop(self.car_cells)
self.navigation = [0] * self.n_cells
# reset other variables
self.reward = 0
self.terminal = False
Agent
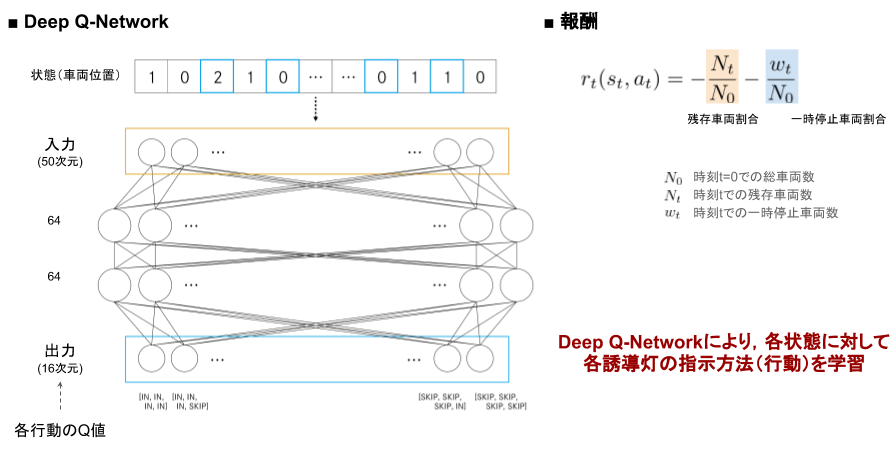
Agentの学習および報酬の設計のイメージは上の図の通り。
状態(車両位置)を入力とし、全結合層を2つはさんで行動(誘導灯指示の組み合わせ)のQ値を出力とする。
報酬は
・総車両数に対する時刻 t での残存車両数の割合
・総車両数に対する時刻 t での一時停止車両数の割合
を用いた。
以上を踏まえたPythonコードは以下の通り。
from collections import deque
import os
import numpy as np
import tensorflow as tf
# it is necessary if tensorflow version > 2.0
import tensorflow.compat.v1 as tf
tf.disable_v2_behavior()
class DQNAgent:
"""
Multi Layer Perceptron with Experience Replay
"""
def __init__(self, enable_actions, environment_name, n_cells):
# parameters
self.name = os.path.splitext(os.path.basename(__file__))[0]
self.environment_name = environment_name
self.enable_actions = enable_actions
self.n_actions = len(self.enable_actions)
self.minibatch_size = 32
self.replay_memory_size = 1000
self.learning_rate = 0.001
self.discount_factor = 0.9
self.exploration = 0.1
self.model_dir = os.path.join(os.path.dirname(os.path.abspath(__file__)), "models")
self.model_name = "{}.ckpt".format(self.environment_name)
self.n_cells = n_cells
# replay memory
self.D = deque(maxlen=self.replay_memory_size)
# model
self.init_model()
# variables
self.current_loss = 0.0
def init_model(self):
# input layer (1 x n_cells)
self.x = tf.placeholder(tf.float32, [None, self.n_cells])
# flatten (n_cells)
x_flat = tf.reshape(self.x, [-1, self.n_cells])
# fully connected layer 1
W_fc1 = tf.Variable(tf.truncated_normal([self.n_cells, 64], stddev=0.01))
b_fc1 = tf.Variable(tf.zeros([64]))
h_fc1 = tf.nn.relu(tf.matmul(x_flat, W_fc1) + b_fc1)
# fully connected layer 2
W_fc2 = tf.Variable(tf.truncated_normal([64, 64], stddev=0.01))
b_fc2 = tf.Variable(tf.zeros([64]))
h_fc2 = tf.nn.relu(tf.matmul(h_fc1, W_fc2) + b_fc2)
# output layer (n_actions)
W_out = tf.Variable(tf.truncated_normal([64, self.n_actions], stddev=0.01))
b_out = tf.Variable(tf.zeros([self.n_actions]))
self.y = tf.matmul(h_fc2, W_out) + b_out
# loss function
self.y_ = tf.placeholder(tf.float32, [None, self.n_actions])
self.loss = tf.reduce_mean(tf.square(self.y_ - self.y))
# train operation
optimizer = tf.train.RMSPropOptimizer(self.learning_rate)
self.training = optimizer.minimize(self.loss)
# saver
self.saver = tf.train.Saver()
# session
self.sess = tf.Session()
self.sess.run(tf.global_variables_initializer())
def Q_values(self, state):
# Q(state, action) of all actions
return self.sess.run(self.y, feed_dict={self.x: [state]})[0]
def select_action(self, state, epsilon):
if np.random.rand() <= epsilon:
# random
indice = np.random.choice(self.n_actions)
return self.enable_actions[indice]
else:
# max_action Q(state, action)
return self.enable_actions[np.argmax(self.Q_values(state))]
def store_experience(self, state, action, reward, state_1, terminal):
self.D.append((state, action, reward, state_1, terminal))
def experience_replay(self):
state_minibatch = []
y_minibatch = []
# sample random minibatch
minibatch_size = min(len(self.D), self.minibatch_size)
minibatch_indexes = np.random.randint(0, len(self.D), minibatch_size)
for j in minibatch_indexes:
state_j, action_j, reward_j, state_j_1, terminal = self.D[j]
action_j_index = self.enable_actions.index(action_j)
y_j = self.Q_values(state_j)
if terminal:
y_j[action_j_index] = reward_j
else:
# reward_j + gamma * max_action' Q(state', action')
y_j[action_j_index] = reward_j + self.discount_factor * np.max(self.Q_values(state_j_1)) # NOQA
state_minibatch.append(state_j)
y_minibatch.append(y_j)
# training
self.sess.run(self.training, feed_dict={self.x: state_minibatch, self.y_: y_minibatch})
# for log
self.current_loss = self.sess.run(self.loss, feed_dict={self.x: state_minibatch, self.y_: y_minibatch})
def load_model(self, model_path=None):
if model_path:
# load from model_path
self.saver.restore(self.sess, model_path)
else:
# load from checkpoint
checkpoint = tf.train.get_checkpoint_state(self.model_dir)
if checkpoint and checkpoint.model_checkpoint_path:
self.saver.restore(self.sess, checkpoint.model_checkpoint_path)
def save_model(self):
self.saver.save(self.sess, os.path.join(self.model_dir, self.model_name))
学習
上で見てきた設定でモデルの学習をおこなった上で実験をおこない、学習しない場合(=誘導灯がすべて入庫指示)と比べてどれほど車両を効率的に制御できているかを確認する。
学習および実験のPythonコードは以下の通り。
import numpy as np
from environment import Parking
from agent import DQNAgent
if __name__ == "__main__":
# parameters
n_epochs = 1000
# environment, agent
env = Parking(test = False)
agent = DQNAgent(env.enable_actions, env.name, env.n_cells)
for e in range(n_epochs):
# reset
frame = 0
loss = 0.0
Q_max = 0.0
env.reset()
state_t_1, reward_t, terminal, state_remain, state_stop = env.observe()
while not terminal:
state_t = state_t_1
# execute action in environment
action_t = agent.select_action(state_t, agent.exploration)
env.execute_action(action_t)
# observe environment
state_t_1, reward_t, terminal, state_remain, state_stop = env.observe()
# store experience
agent.store_experience(state_t, action_t, reward_t, state_t_1, terminal)
# experience replay
agent.experience_replay()
# for log
frame += 1
loss += agent.current_loss
Q_max += np.max(agent.Q_values(state_t))
print("EPOCH: {:03d}/{:03d} | FRAME: {:d} | LOSS: {:.4f} | Q_MAX: {:.4f}".format(
e, n_epochs - 1, frame, loss / frame, Q_max / frame))
# save model
agent.save_model()
import matplotlib.pyplot as plt
import argparse
import datetime
import os
from environment import Parking
from agent import DQNAgent
import csv
import pprint
if __name__ == "__main__":
# args
parser = argparse.ArgumentParser()
parser.add_argument("-m", "--model_path")
parser.add_argument("--load_model", default=True) # 学習したモデル使用→True, 不使用→False
parser.add_argument("-s", "--save", dest="save", action="store_true")
parser.set_defaults(save=False)
args = parser.parse_args()
# environmet, agent
env = Parking(test = True)
agent = DQNAgent(env.enable_actions, env.name, env.n_cells)
if args.load_model:
agent.load_model(args.model_path)
# variables
score = 0
state_t_1, reward_t, terminal, state_remain, state_stop = env.observe()
result_state = []
result_remain = []
result_stop = []
n_cars = state_remain
while not terminal:
result_state.append(list(state_t_1))
result_remain.append(state_remain)
result_stop.append(state_stop)
state_t = state_t_1
# execute action in environment
if args.load_model:
action_t = agent.select_action(state_t, 0.0)
else:
action_t = [1,1,1,1]
env.execute_action(action_t)
state_t_1, reward_t, terminal, state_remain, state_stop = env.observe()
result_remain.append(state_remain)
result_stop.append(state_stop)
print("conversion time = " + str(len(result_remain))) # total time
print("average time = " + str(sum(result_remain) / n_cars)) # average parking time
print("extra stopping time = " + str(sum(result_stop) - n_cars)) # extra stopping time
# output for csv
with open('output/result.csv', 'a') as f:
writer = csv.writer(f)
writer.writerow([len(result_remain), sum(result_remain) / n_cars, sum(result_stop) - n_cars])
# mkdir for output
dirname_n_remain = "output/figure/n_remain/"
dirname_n_stop = "output/figure/n_stop/"
dirname_state = "output/figure/state/"
os.makedirs(dirname_n_remain, exist_ok=True)
os.makedirs(dirname_n_stop, exist_ok=True)
os.makedirs(dirname_state, exist_ok=True)
# file name is date+time
now = datetime.datetime.now()
n_remain_filename = dirname_n_remain + now.strftime('%Y%m%d_%H%M%S') + '.png'
n_stop_filename = dirname_n_stop + now.strftime('%Y%m%d_%H%M%S') + '.png'
state_filename = dirname_state + now.strftime('%Y%m%d_%H%M%S') + '.png'
# make the graph of number of remaining cars
epoch = range(len(result_remain))
plt.figure()
plt.xlabel("time")
plt.ylabel("number of remained cars")
plt.plot(epoch, result_remain);
plt.show()
# make the graph of stopping cars
epoch = range(len(result_stop))
plt.figure()
plt.xlabel("time")
plt.ylabel("number of stopping cars")
plt.plot(epoch, result_stop);
plt.show()
# make the figure of state transition
plt.figure()
plt.title("State Transition")
plt.imshow(result_state, cmap="binary")
plt.show()
結果
残存車両数の推移
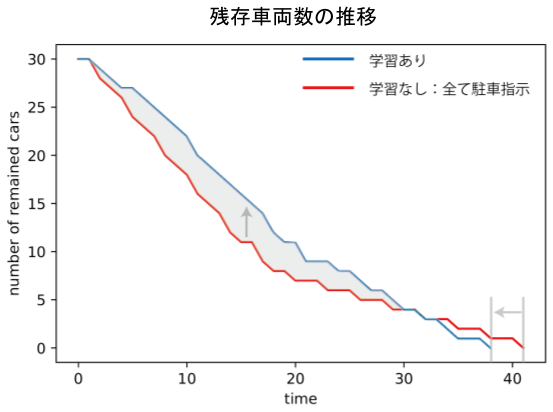
残存車両数の推移は上の図の通り(初期車両数30)。
学習をおこなった場合、初期段階では車がなかなか減らないが、全ての車が駐車完了するまでの時間は短縮できた。これは、特定の駐車場に偏った場合に起こる渋滞を防ぐために、いくつかの車について「あえて見送り」という指示を出していることに起因する。一部車両の利益を犠牲にして社会最適をとった形だ。
状態推移(初期車両数30)
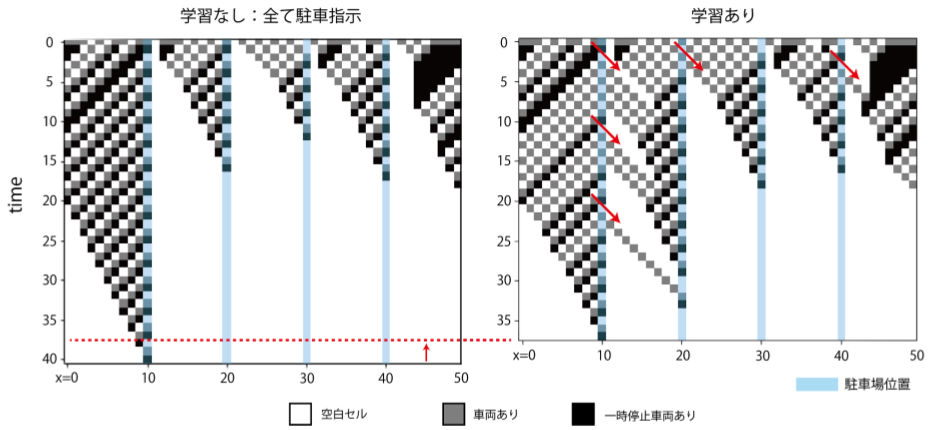
実際の車両の動きがどうなっているのか、状態遷移の様子を見てみる。縦軸方向が時間、横軸方向が各時刻での状態。t=0での初期状態を与えて、時間発展させた際の状態変化を下方向に積み上げたもの。
初期車両数30の場合の状態遷移は上の図の通り。残存車両数の推移で見たように、いくつかの車両に対し「あえて見送り」の指示を与えていることで将来の渋滞が緩和され、結果的に全車両の駐車完了が早まっている。
状態推移(初期車両数20)
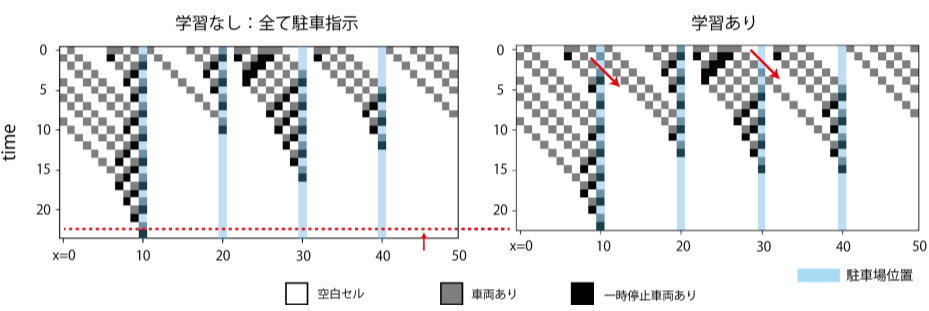
初期車両数20の場合の状態遷移は上の図の通り。初期車両数30の場合と同様に、「あえて見送り」を指示することで将来の渋滞が緩和され、結果的に全車両の駐車完了が早まっている。このことから、車両数に対してある程度学習は頑健であることがわかる。
状態遷移(初期車両数10)
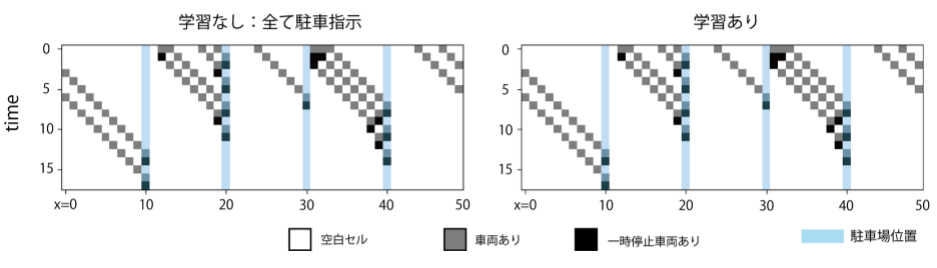
初期車両数10の場合の状態遷移は上の図の通り。初期車両数が少ない場合は渋滞が発生せず、「あえて見送り」の指示をする必要がないと判断している。
結論
・駐車行動を伴う道路空間をセルオートマトンでシンプルに記述した。
・「見つけた駐車場にとりあえず入庫する」戦略はかえって全車両が駐車完了する時間を増大させてしまうことがある。
・駐車場への入庫を指示する誘導灯を導入し、DQNを用いて学習することで、全車両が駐車完了する時間を短くできる。
-
Donald C. Shoup (2006), Cruising for parking, Transport Policy, vol.13 issue.6, pp479-486. ↩
-
Simulation of Urban MObilityの略。交通流などを扱えるオープンソースのシミュレータ。https://github.com/eclipse/sumo ↩
-
今回の実装はDQNの基本的な実装例を提示している https://github.com/algolab-inc/tf-dqn-simple を参考におこなった。Agent以降のコードも同様。 ↩