はじめに
今回はオープンソースの半導体デバイスシミュレータであるTiberCadを用いて、
1次元GaAs / AlGaAs量子井戸のSchrödinger–Poisson 連成解析を行い
電子のサブバンドエネルギー準位解析をためしてみます。
この事例はTiberCadのexample 8の内容になります。
解析の全体像
今回行う解析は以下の流れです。
1D メッシュで量子井戸構造を定義(.geo)
↓
材料・ドーピング・量子計算領域を定義(Device)
↓
ひずみ解析(elasticity)
↓
Poisson + Drift-Diffusion
↓
Schrödinger 方程式(有効質量近似)
↓
Poisson–Schrödinger 自己無撞着計算
量子井戸の 1D 構造定義(quantum_poisson.geo)
こちらが今回検討する1次元量子井戸です。
x=-100 -20 -10 +10 +20 +100
|---------|------|========|------|---------|
AlGaAs AlGaAs GaAs AlGaAs AlGaAs
中央:GaAs 量子井戸(幅 20 nm)
両側:Al₀.₃Ga₀.₇As バリア
この.geoファイルをgmsh上に呼び出してメッシュ生成後に.mshで保存すればOKです。
*但し、example 8フォルダにはメッシュ生成後のファイルも格納済み
Device 定義:材料・ドーピング(quantum_poisson.tib)
以下がスクリプトになります。
このスクリプトは、GaAs/AlGaAs 量子井戸構造を対象に、一次元の Schrödinger–Poisson 連成解析を行う設定である。中央の GaAs 井戸と高濃度ドープされた AlGaAs バリアからなる変調ドープ構造を定義し、電子が井戸内に量子化される状況を解析する。まず格子不整合によるひずみを計算し、その結果を反映した Poisson–Drift–Diffusion 計算によって電位とバンド構造を求め、伝導帯の電子についてはシュレーディンガー方程式を解き、サブバンドエネルギー、波動関数、量子密度を算出する。これらを Poisson 方程式と自己無撞着に連成することで、外部電圧を印加しない平衡状態での量子井戸中の電子状態を求めてます。
もちろん、電圧をかけ条件での計算もできますが、今回はテスト的に歪みも取り込んだ形で、シミュレーションを実行します。
#Example 8: 1D Schroedinger-Poisson
Device
{
meshfile = quantum_poisson.msh
mesh_units = 1e-9
Region well
{
material = GaAs
Doping
{
density = 1e15
type = donor
level = 0.025
}
}
Region buffer1
{
mesh_regions = ( barrier1_a,barrier1_q)
material = AlGaAs
x = 0.3
Doping
{
density = 1e17
type = donor
level = 0.025
}
}
Region buffer2
{
mesh_regions = (barrier2_a, barrier2_q )
material = AlGaAs
x = 0.3
Doping
{
density = 1e17
type = donor
level = 0.025
}
}
Cluster Quantum_1
{
regions = (well ,barrier1_q, barrier2_q )
}
}
Module elasticity
{
name = strain
regions = all
plot = (Strain, Stress, Displacement )
Physics
{
body_force lattice_mismatch
{
reference_material = GaAs
}
}
Contact substrate
{type = clamp}
}
Module driftdiffusion
{
name = dd
regions = all
coupling = poisson
plot = (Polarization, Ec, Ev, eQFermi, hQFermi, ElField, eDensity, hDensity,
CurrentDensity, ContactCurrent, eMobility, hMobility)
Physics
{
valence_band
{
density_of_states bulk_kp
{
strain_simulation = strain
}
}
conduction_band
{
density_of_states quantum
{
quantum_simulation = quantum_el
barrier_regions = (buffer1, buffer2)
classical_DOS bulk_kp
{
strain_simulation = strain
}
}
}
recombination srh {}
mobility doping_dependent {}
}
}
Module efaschroedinger
{
name = quantum_el
regions = Quantum_1
plot = (ProbabilityDensity, EigenEnergy, QuantumDensity)
num_electron_states = 22
poisson_simulation = dd
strain_simulation = strain
Physics
{
model = conduction_band
}
}
Module selfconsistent
{
name = poisson_schroedinger
solve = (quantum_el, dd)
max_iterations = 10
absolute_tolerance = 1e-3
relative_tolerance = 1e-8
monitor = true
#xmonitor = true
}
Simulation
{
dimension = 1
temperature = 300
solve = (strain, dd, poisson_schroedinger)
resultpath = output
output_format = grace
}
実行結果
今回もExample 8フォルダに移動したら下記のコマンドを実行することで、解析を実行できます。
tibercad quantum_poisson.tib
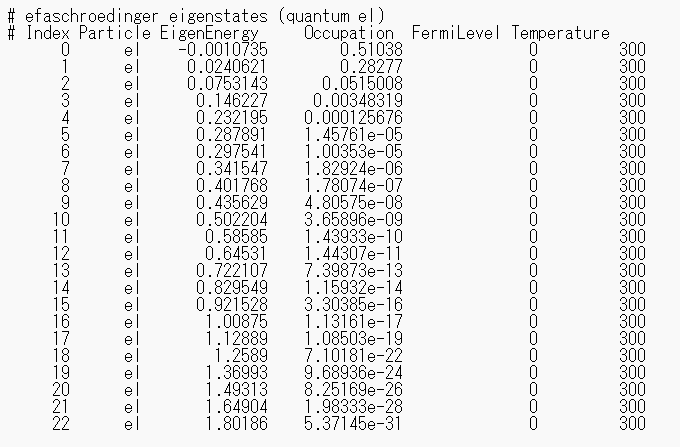
解析を実行すると、指定した温度条件(今回は300 K)における電子のサブバンドの固有エネルギーと占有率が出力されます。
※本記事は筆者個人の見解であり、所属組織の公式見解を示すものではありません。
問い合わせ
光学シミュレーションソフトの導入や技術相談、
設計解析委託をお考えの方はサイバネットシステムにお問合せください。
光学ソリューションサイトについては以下の公式サイトを参照:
👉 光学ソリューションサイト(サイバネット)
光学分野のエンジニアリングサービスについては以下の公式サイトを参照:
👉 光学エンジニアリングサービス(サイバネット)