[技術メモ]光変調器の小信号の周波数応答を求める式について

🔍はじめに

近年、データセンター間通信の高速化やAI向け計算リソースの増大に伴い、光通信技術に新規参入する企業が急速に増えています。 それに伴い、光変調器やレーザ、受光器といった光デバイスの基礎原理から、実際の評価・シミュレーション手法までをエンジニアが自ら理解し、最適化する機会も増えてきました。
特に、進行波電極の光変調器の小信号周波数応答（Small-Signal Frequency Response） は、デバイスの帯域幅・変調効率・ドライバ回路との整合性を評価するうえで欠かせない指標です。 しかし、文献によって表記が微妙に異なっていたり、分かりにくい部分も多くあります。
本記事では、光変調器の小信号周波数応答を求める際に用いられる代表的な式と、その導出方法について、実務寄りに整理します。 これから光通信デバイス設計に携わる方や、シミュレーション／評価の理解を深めたい方の助けになれば幸いです。
ここで整理する式は以下の文献に基づいた内容となっております(Giovanni Ghione, "Semiconductor Devices for High-Speed Optoelectronics" Cambridge University Press 2009)。

🚀進行波電極のマッハツエンダー型光変調器とは？

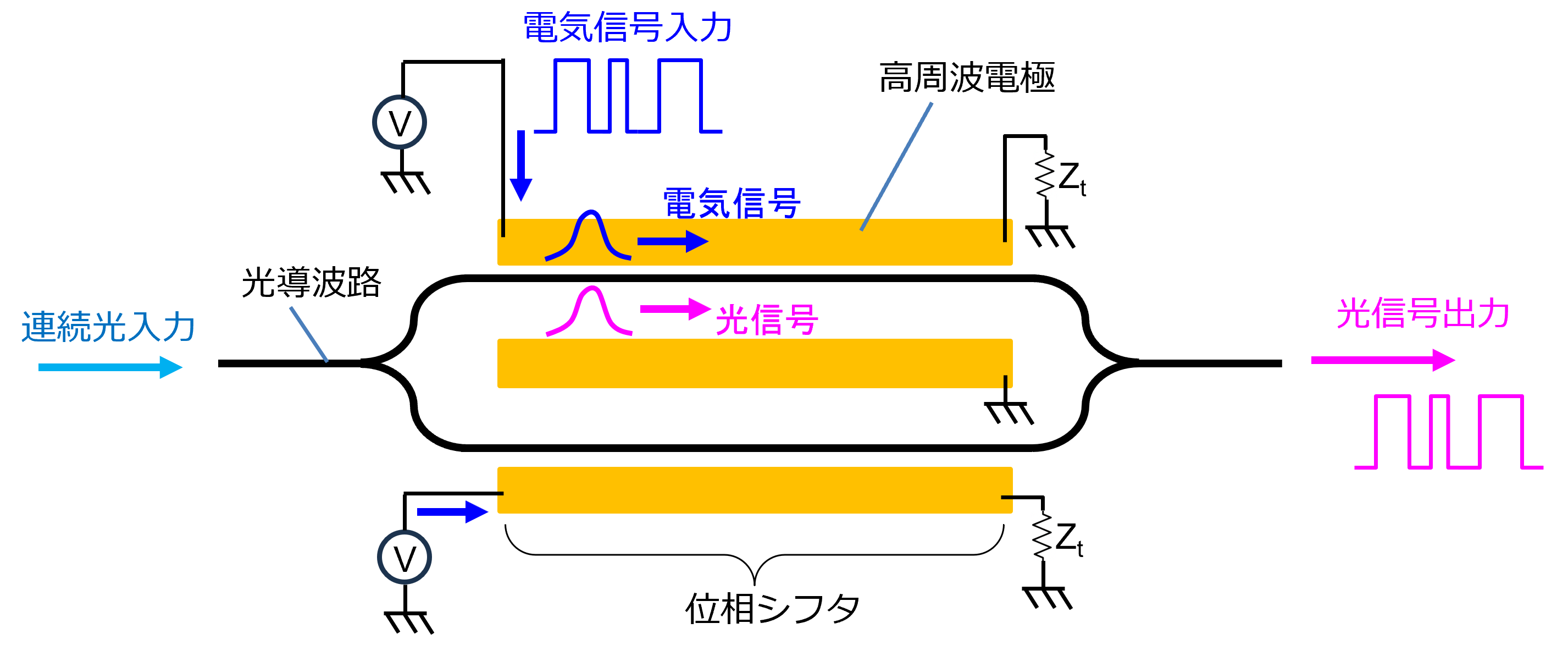
進行波電極の光変調器とは、電気信号が電極上を光と同じ方向へ進みながら変調を行う構造を持つ光変調器のことです。電気と光の位相速度を近づけることで、高帯域・低損失な変調を実現できる点が特徴です。特に、高速通信向けのLiNbO₃やSiフォトニクスのマッハツェンダ変調器（MZM）で広く採用されています。

✨小信号応答の解析式の求め方

ここでは、先ほど挙げた書籍に則って解説していきます。
以下が式の導出にあたり考えている系になります。マッハツェンダ型光変調器の片側部分の位相シフタを取り出しています。

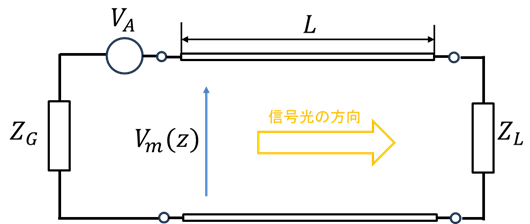
1. 伝送線路モデルと目的
進行波電極のマッハツェンダ変調器（MZM）は、RF 電極が伝送線路として動作し、その上を進む電圧波が光導波路の屈折率を変調します。
ここで求めたいのは、
RF ソース電圧の複素振幅 VAを入力とし出力光の位相変調量 Δϕ(ω)を出力とする
小信号周波数応答
$$
H(\omega) \equiv \frac{\Delta \phi(\omega)}{V_A}
$$
です。最終的には、規格化変調度
$$
m(\omega) = \left| \frac{H(\omega)}{H(0)} \right|
$$

2. RF 電圧波 vm (z,t)
RF 電極は損失を持つ準 TEM 伝送線路とみなします。
その電圧は、進行波と反射波の重ね合わせで
$$
v_m(z,t) = V^{+} e^{j\omega (t - z/v_m) - \alpha_m z}
+
V^{-} e^{j\omega (t + z/v_m) + \alpha_m z}
$$

と書けます。

• v_m：RF の位相速度
• α_m：RF の振幅減衰定数
• V⁺, V⁻：前進波・後進波の複素振幅

後で扱いをまとめるために、
RF の複素伝搬定数
$$
\gamma_m = \alpha_m + j \beta_m
$$

としておきます。

3. RF による屈折率変調
電気光学効果により、屈折率の変化量 Δnは局所電圧に比例すると仮定します
$$
\Delta n(z,t) = a, v_m(z,t)
$$

ここで aは EO 係数などを含む比例定数です。
一方、光パルスは光群速度 v_0で z=0から z=Lまで伝搬します。
光が位置 zを通過するときの時間は
$$
t(z) = t_0 + \frac{z}{v_0}
$$

ですが、出力端に到達する時間 t2=t0+L/v0を基準に書き換えると
$$
t(z) = t_2 - \frac{L}{v_0} + \frac{z}{v_0}
$$

となります。
つまり、光は、「自分が通過するタイミング t(z)における局所電圧」
" " vm(z,t(z))を見ながら、区間 0≤z≤Lを進んでいきます。

4. 屈折率分布を積分して位相変調を求める
光の出力場を E(t2)とすると、屈折率変調 Δnによる総位相変化は
$$
\Delta \phi(\omega)
= k_0 \int_{0}^{L} \Delta n\left(z, t(z)\right)\ dz
= k_0 a \int_{0}^{L} v_m\left(z, t(z)\right)\ dz
$$
で与えられます。
ここで k0=2π/λ0は真空波数です。
式 (1) を (4) に代入し、時間引数に (3) を入れて積分すると
$$
\Delta \phi(\omega)
= k_0 a\ e^{j\omega (t_2 - L/v_0)}
\left[
\frac{
V^{+}\ e^{\ j\omega (L/v_0 - L/v_m) - \alpha_m L} - 1
}{
j\omega \left( \frac{1}{v_0} - \frac{1}{v_m} \right) - \alpha_m
}
+
\frac{
V^{-}\ e^{\ j\omega (L/v_0 + L/v_m) + \alpha_m L} - 1
}{
j\omega \left( \frac{1}{v_0} + \frac{1}{v_m} \right) + \alpha_m
}
\right]
$$

が得られます。

5. 電気–光学定数で書き換える
EO 係数 r33とオーバラップ係数 Γmoを使うと、比例定数 k0*aは
$$
k_0 a
= \frac{\pi n_e^{3} r_{33}}{\lambda_0}
\frac{\Gamma_{mo} L}{G}
$$
と書けます。
ここで

• n_e：光の有効屈折率
• G：MZM のバイアスに関する幾何学的係数（たとえば push–pull の 2 倍など）

これを上記の式に代入しておきます。

6. 伝送線路の境界条件から V⁺, V⁻ を求める

次に、「電源側 z=0」と「負荷側 z=L」の境界条件を課して、
前進波・後進波の振幅 V⁺, V⁻ を開放電圧 V_A とインピーダンスで表します。

• ソースインピーダンス： Z_G
• 負荷インピーダンス： Z_L
• 線路の特性インピーダンス： Z₀

とすると、線路電圧・電流は …

$$ v_m(z,t) = V^{+} e^{-\gamma_m z + j\omega t} + V^{-} e^{\gamma_m z + j\omega t} $$

$$
i_m(z,t)
= \frac{V^{+}}{Z_0} e^{-\gamma_m z + j\omega t}- \frac{V^{-}}{Z_0} e^{\gamma_m z + j\omega t}
$$

境界条件
$$
v_m(0,t) = V_A e^{j\omega t} - Z_G\ i_m(0,t)
$$

$$
v_m(L,t) = Z_L\ i_m(L,t)
$$
を課して連立方程式を解くと、波の振幅は
$$
V^{+}
= \frac{1}{1 - \Gamma_L \Gamma_G e^{-2\gamma_m L}}
\frac{Z_0}{Z_0 + Z_G}
V_A
$$

$$
V^{-}
= \frac{\Gamma_L e^{-2\gamma_m L}}{1 - \Gamma_L \Gamma_G e^{-2\gamma_m L}}
\frac{Z_0}{Z_0 + Z_G}
V_A
$$
となります。
ここで、
$$
\Gamma_L = \frac{Z_0 - Z_L}{Z_0 + Z_L},
\qquad
\Gamma_G = \frac{Z_0 - Z_G}{Z_0 + Z_G}
$$
は負荷側・ソース側の反射係数です。

7. H(ω)の評価式
$$
\Delta \phi(\omega)
= H(\omega)\ V_A e^{j\omega t_2}
$$
と書けます。ここで
$$
H(\omega)
= \frac{\pi n_e^{3} r_{33}}{\lambda_0}
\frac{\Gamma_{mo} L}{G}
\frac{Z_0 e^{-\gamma_m L}}{Z_0 + Z_G}
\frac{
F(u_{+}) + \Gamma_L F(u_{-})
}{
1 - \Gamma_L \Gamma_G e^{-2\gamma_m L}
}
$$
が求めたかった光位相変調の周波数応答です。
ここで、
$$
F(u) = \frac{1 - \exp(u)}{u}
$$

$$
u_{\pm}(\omega)
= j(\pm \beta_m - \beta_0)L
\pm\alpha_m L=
\pm\alpha_m L+ j\frac{\omega}{c_0}(\pm n_m - n_0)L
$$
ここで、n_oは光導波路の群屈折率、n_mは高周波の伝送線路の位相屈折率になります。

8. 規格化変調度 m(ω)
最後に、DC（ω=0）での変調量で規格化した変調度の周波数応答
$$
m(\omega)
= \left| \frac{\Delta \phi(\omega)}{\Delta \phi(0)} \right|
= \left| \frac{H(\omega)}{H(0)} \right|
$$
を定義します。
電気側の等価回路を使って整理すると、
$$
m(\omega)
= \frac{R_L + R_G}{R_L}
\left|
\frac{Z_{\mathrm{in}}}{Z_{\mathrm{in}} + Z_G}
\right|
\left|
\frac{
(Z_L + Z_0)\ F(u_{+})
+
(Z_L - Z_0)\ F(u_{-})
}{
(Z_L + Z_0)\ e^{\gamma_m L}
+
(Z_L - Z_0)\ e^{-\gamma_m L}
}
\right|
$$

ここでZinは以下の式になります。
$$
Z_{\mathrm{in}}
= Z_{0}\frac{Z_{L} + Z_{0}\tanh(\gamma_{m} L)}
{Z_{0} + Z_{L}\tanh(\gamma_{m} L)}
$$
となります。
高周波の伝送線路の位相屈折率や特性インピーダンスを求めるにはHFSSなどの高周波シミュレータなどを用いて得られたSパラメータの結果を変換して求めることができます。以下に参考となるサイトを挙げておきます(https://optics.ansys.com/hc/en-us/articles/360042097393-Metamaterial-parameter-extraction-Smith)。
但し、50 Ohm基準とする場合は、式で求めた結果に50 Ohmを掛ける必要があります。また、屈折率も2πの整数倍の不定性に注意して解析する必要があります。

※本記事は筆者個人の見解であり、所属組織の公式見解を示すものではありません。

問い合わせ

光学シミュレーションソフトの導入や技術相談、
設計解析委託をお考えの方はサイバネットシステムにお問合せください。

光学ソリューションサイトについては以下の公式サイトを参照：
👉 光学ソリューションサイト(サイバネット)

光学分野のエンジニアリングサービスについては以下の公式サイトを参照：
👉 光学エンジニアリングサービス(サイバネット)