Pythonで分散分析(対応なし・二元配置)
目的
SPSSで実施していた対応なしの二元配置分散分析を無料のPythonで実行すること.
参考にしたwebページの紹介
本記事の内容のほとんどはErik Marsja「Three ways to do a two-way ANOVA with Python」の記事を参考にさせていただきました.
また,二要因分散分析の復習は統計検定を理解せずに使っている人のためにⅢのページを参考にしました.
途中で行う多重比較についてはこのPythonで統計学を学ぶ(6)というページから関数を使わせてもらっています.
以下に書いてあること
Pythonで対応なしの二元配置分散分析を行った道筋を,サンプルデータを使いながらまとめてみました.
サンプルデータについて
サンプルデータは600人の若年男性を対象に100m走のタイムを計測した設定です.このとき,「シューズの違い」及び「走ったトラックの違い」の2つの要因が100m走のタイムに及ぼす影響を,pythonで二元配置分散分析をしながら統計的にみていきます.
要因は
シューズ条件:A社製シューズ[A],B社製シューズ[B],N社製シューズ[N]の3水準
トラック条件:グラウンド[Ground],タータン[Tartan]の2水準(陸上トラックに使用されているコルクのような見た目の材質は「タータン」と呼ぶんだと陸上経験者の友人から教わりました)
の2つであり,条件数は2要因×3水準=6条件です.各条件につき100名が走っている設定です.
| 対象 | 若年男性600名 |
|---|---|
| 要因 | シューズ(3水準),トラック(2水準) |
| 指標 | 100m走ったタイム[s] |
| 条件数 | (シューズ3水準)×(トラック2水準)=6条件(600人集めて各条件に付き100名ずつ走ってもらった設定) |
ライブラリのインポート
# 数値計算に使うライブラリ
import pandas as pd
import numpy as np
import scipy as sp
from scipy import stats as st
# グラフを描画するライブラリ
from matplotlib import pyplot as plt
import seaborn as sns
sns.set()
# 統計モデルを推定するライブラリ
import statsmodels.formula.api as smf
import statsmodels.api as sm
import statsmodels.stats.anova as anova # 分散分析やるライブラリ
from statsmodels.stats.multicomp import pairwise_tukeyhsd # Tukeyの多重比較やるライブラリ
from statsmodels.graphics.factorplots import interaction_plot
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
# 表示桁数の指定
%precision 3
# グラフをjupyter notebook内に表示させるための指定
%matplotlib inline
サンプルデータの読み込み
サンプルデータも上げておきます.
file = "Runtime.csv"
data = pd.read_csv(file)
data.head(10) #データの中身を確認(先頭10行のみ)
Unnamed: 0 ShoesMaker Track Time
0 0 A Ground 15.624345
1 1 A Ground 13.388244
2 2 A Ground 13.471828
3 3 A Ground 12.927031
4 4 A Ground 14.865408
5 5 A Ground 11.698461
6 6 A Ground 15.744812
7 7 A Ground 13.238793
8 8 A Ground 14.319039
9 9 A Ground 13.750630
グラフの表示
fig = interaction_plot(data.ShoesMaker, data.Track, data.Time, # (横軸にする要因(水準多い方),系列にする要因(水準少ない方),評価指標)
colors=['red','blue'], markers=['D','^'], ms=10)
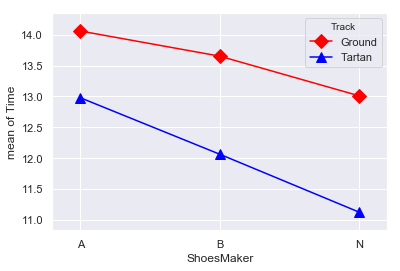
グラフの解釈
平均時間が短い=速く走れている
ということですので,横軸のシューズごとにみると,N社のシューズが他のシューズと比べて速く走れるシューズのようです.
また系列ごと(赤い線と青い線)にみると,Taratanで走ったほうが速く走れそうです.
加えて,N社製のシューズかつTaratanで走ると,なんだかますます速く走れそうであること(相乗効果がありそうなこと)が,グラフの傾き具合から言えるかもしれません.換言すれば,シューズ×トラックの交互作用もあるかもしれません.
そこで,二元配置の分散分析を実施します.
二元配置分散分析の実施
formula = 'Time ~ (Track) + (ShoesMaker) + (Track):(ShoesMaker)'
model = ols(formula, data).fit()
aov_table = anova_lm(model, typ=2)
aov_table.columns = ["平方和","自由度","F値","p値"] #列名を日本語に差し替え
print(aov_table) #被験者間効果の検定結果を出力
平方和 自由度 F値 p値
Track 345.591633 1.0 344.753535 4.987607e-61
ShoesMaker 211.505336 2.0 105.496206 6.228932e-40
ShoesMaker:Track 16.505274 2.0 8.232623 2.973539e-04
Residual 595.444018 594.0 NaN NaN
シューズやトラックで主効果がみられました.さらにシューズ条件とトラック条件の間で交互作用がみられました( p < 0.05).
交互作用がみられた場合,全群の多重比較を実施していくのが王道なようです.
交互作用が無かった場合は,各要因ごとの水準間の平均値で(他方の要因は一旦置いといて)群間比較すれば良いそうです.
補足:anova_lmについて
交互作用あり→全群の多重比較(今回はシューズA時のトラックの違いのみ)
多重比較については対応なしの一元配置分散分析のときも少しまとめましたので,今回はシューズAのときのトラック条件間の比較のみメモしておきます.
MakerATrackG = data[(data.ShoesMaker=="A")&(data.Track=="Ground")] # dataからShoesMakerがAかつTrackがGroundのものを抽出
MakerATrackT = data[(data.ShoesMaker=="A")&(data.Track=="Tartan")] # dataからShoesMakerがAかつTrackがTartanのものを抽出
MakerATrackG.head(10) # 中身の確認
Unnamed: 0 ShoesMaker Track Time
0 0 A Ground 15.624345
1 1 A Ground 13.388244
2 2 A Ground 13.471828
3 3 A Ground 12.927031
4 4 A Ground 14.865408
5 5 A Ground 11.698461
6 6 A Ground 15.744812
7 7 A Ground 13.238793
8 8 A Ground 14.319039
9 9 A Ground 13.750630
Tukeyの多重比較を実施
多重比較するための関数を用意
以下の関数を使います( Pythonで統計学を学ぶ(6) 内の「 In [42] # 参考: 関数にしてみた」より)
# 関数(グループ数の羅列,グループ名)
def tukey_hsd( ind, *args ): # 第1引数:名称のリスト(index), 第2引数以降: データ(*args: 複数の引数をタプルとして受け取る)
from statsmodels.stats.multicomp import pairwise_tukeyhsd
data_arr = np.hstack( args ) # 配列の結合をhstackでしているらしい.水平方向(新しく列を増やしている方向)に結合.
ind_arr = np.array([])
for x in range(len(args)):
ind_arr = np.append(ind_arr, np.repeat(ind[x], len(args[x]))) # ind_arrの配列の最後にnp.repeat()を加える
# np.repeat(A,N)は配列A内の各要素をN回繰り返す
print(pairwise_tukeyhsd(data_arr,ind_arr))
A社製シューズを履いた時のトラック間の違いを比較
tukey_hsd(list('GT') , MakerATrackG['Time'],MakerATrackT['Time'])
Multiple Comparison of Means - Tukey HSD,FWER=0.05
=============================================
group1 group2 meandiff lower upper reject
---------------------------------------------
G T -1.0809 -1.3553 -0.8066 True
---------------------------------------------
以上より,シューズAのときのGurand-Tartan間に有意差がありそうです.
同じことをシューズBのときのTrackごと,シューズNのときのTrackごとに実施し,要因を変えてGroundのときのシューズごと,TartanのときのTrackごとに多重比較を実施してやれば全群の多重比較が網羅できると思います.
結論
Pythonで対応なしの二元配置の分散分析ができました!
終わりに
ここまでやっといてなんですが,scipy公式(多分)は
For many more stat related functions install the software R and the interface package rpy.
統計にまつわるその他の関数については,Rやrpyというパッケージ(Rとやり取りできるらしい)をインストールしましょう
とのことでしたので,分散分析関連もRの力を借りた方が良いのかもしれません(無念).