Pythonで分散分析(対応なし・一元配置の分散分析)
前提条件
Python3を使って,Jupyter notebookで作業しています.
筆者は,一か月ぐらい前に研究室の優秀な優秀な後輩達に連れられてPythonに触れ
そののちに生まれて初めてMarkdown記法やQiitaを知った,浅学の中の浅学な人間です.
至らぬ点も多くあるかと思います.ご了承ください.
目的
SPSSで実施していた一元配置の分散分析を無料のPythonでぱいーんと実行すること
(一元配置の分散分析については,手元のデータを使ってそれらしい結果を導けたため
記憶がフレッシュなうちに投稿)
参考にしたwebページの紹介
本記事の内容は,このwebページを参考にさせていただいております.
Pythonで統計学を学ぶ(6)
また,以下のwebページは統計手法のおさらいで非常に参考になりました.
統計検定を理解せずに使っている人のためにⅠ
統計検定を理解せずに使っている人のためにⅡ
統計検定を理解せずに使っている人のためにⅢ
導入
以下に,適当なデータを使いながら,Pythonで「対応なしの一元配置分散分析」を実施する流れを整理しました.
ライブラリ類をインポート
# 数値計算に使うライブラリ
import pandas as pd
import numpy as np
import scipy as sp
from scipy import stats as st
# グラフを描画するライブラリ
from matplotlib import pyplot as plt
import seaborn as sns
sns.set()
# 統計モデルを推定するライブラリ
import statsmodels.formula.api as smf
import statsmodels.api as sm
import statsmodels.stats.anova as anova # 分散分析するライブラリ
from statsmodels.stats.multicomp import pairwise_tukeyhsd # Tukeyの多重比較するライブラリ
# 表示桁数の指定
%precision 3
# グラフをjupyter notebook内に表示させるための指定
%matplotlib inline
データの読み込み
使用するデータを配列で読み込み
以下の4つの配列は,4つの学校から8名呼び出して同じ100点満点のテストをさせた際の得点のイメージです.
これから__学校の違いがテストの得点に及ぼす影響__について,分析します.
W校 = np.array([66, 62, 80, 50, 57, 68, 73, 65])
X校 = np.array([62, 60, 66, 63, 55, 53, 59, 63])
Y校 = np.array([65, 60, 78, 52, 59, 66, 73, 64])
Z校 = np.array([52, 59, 44, 67, 47, 53, 58, 49])
tdata = pd.DataFrame({'W校':W校, 'X校':X校, 'Y校':Y校, 'Z校':Z校})
tdata
W校 X校 Y校 Z校
0 66 62 65 52
1 62 60 60 59
2 80 66 78 44
3 50 63 52 67
4 57 55 59 47
5 68 53 66 53
6 73 59 73 58
7 65 63 64 49
データをこねこねする作業
要因がもっと増えたりしてくると,こねこねしがいがあります.
ラベルの変更
tdata.columns = ["W高校","X高校","Y高校","Z高校"] #列名の変更(”校”を”高校”に変更)
tdata.index = [1,2,3,4,5,6,7,8] #行名の変更
tdata
W高校 X高校 Y高校 Z高校
1 66 62 65 52
2 62 60 60 59
3 80 66 78 44
4 50 63 52 67
5 57 55 59 47
6 68 53 66 53
7 73 59 73 58
8 65 63 64 49
データの確認
tdata.shape # (行数,列数)と,タプルで返す
tdata.info() # 列のカラム名と中身の情報
type(tdata) # データの型の確認
type(tdata["W高校"])# 列ごとにも型を確認
tdata.head(5) #先頭5行確認
tdata.tail(5) #後ろ5行確認
(割愛)
tdata.describe() # 記述統計
W高校 X高校 Y高校 Z高校
count 8.00000 8.00000 8.000000 8.000000
mean 65.12500 60.12500 64.625000 53.625000
std 9.23406 4.35685 8.140507 7.443837
min 50.00000 53.00000 52.000000 44.000000
25% 60.75000 58.00000 59.750000 48.500000
50% 65.50000 61.00000 64.500000 52.500000
75% 69.25000 63.00000 67.750000 58.250000
max 80.00000 66.00000 78.000000 67.000000
行と列の入れ替え(必要に応じて)
#Data.TもしくはData.transpose())
tdata_Trans = tdata.transpose()
tdata_Trans
1 2 3 4 5 6 7 8
W高校 66 62 80 50 57 68 73 65
X高校 62 60 66 63 55 53 59 63
Y高校 65 60 78 52 59 66 73 64
Z高校 52 59 44 67 47 53 58 49
分析手法の決定
正規性の検定
st.shapiro(tdata) #Shapiro-Wilk検定(統計量,p値)
(0.982, 0.862)
検定の結果,4群のデータがそれぞれ正規母集団からサンプリングされたものであるという帰無仮説を棄却できなかったため
4群とも「正規母集団からサンプリングされたものである」という帰無仮説を採択します.
等分散性の検定
st.bartlett(tdata["W高校"],tdata["X高校"],tdata["Y高校"],tdata["Z高校"]) # Bartlett検定
BartlettResult(statistic=3.5539244341193403, pvalue=0.3138353536500928)
Shapiro-Wilk検定の結果より,正規分布に従っていそうなので,Leveneの検定ではなくBartlett検定を実施しました.
検定の結果,「4つの群からなる標本について分散が各群とも等しい」という帰無仮説を棄却できなかったため
「4つの群からなる標本について分散が各群とも等しい」という帰無仮説を採択します.
検定結果より,パラメトリック検定である分散分析を用います.
(今回はデータ数が少ないかもしれませんが...)
対応なしの一元配置分散分析
f, p = st.f_oneway(tdata["W高校"],tdata["X高校"],tdata["Y高校"],tdata["Z高校"])
print("F=%f, p-value = %f"%(f,p))
F=4.024871, p-value = 0.016860
分散分析の結果 p < 0.05 より
「4つの学校のテストの得点の平均に差はない」という帰無仮説が棄却されました.
したがって4つの学校のテストの得点の平均に差がないとは言えない,
つまり
学校の違いがテストの得点に影響を及ぼしている可能性がある
と言えそうです.
その後の検定(多重比較)
Tukeyの検定で多重比較を行い
具体的に「どの学校とどの学校に得点差があるのか」をみていきます.
W高校 = tdata["W高校"]
X高校 = tdata["X高校"]
Y高校 = tdata["Y高校"]
Z高校 = tdata["Z高校"]
以下の関数を使います( Pythonで統計学を学ぶ(6) 内の「 In [42] # 参考: 関数にしてみた」より)
# 関数(グループ数の羅列,グループ名)
def tukey_hsd( ind, *args ):
# 第1引数:名称のリスト(index), 第2引数以降: データ (*args: 複数の引数をタプルとして受け取る)
from statsmodels.stats.multicomp import pairwise_tukeyhsd
data_arr = np.hstack( args )
# 配列の結合をhstackでしているらしい.水平方向(新しく列を増やしている方向)に結合.horizontalのhかと
ind_arr = np.array([])
for x in range(len(args)):
ind_arr = np.append(ind_arr, np.repeat(ind[x], len(args[x])))
# ind_arrの配列の最後にnp.repeat()を加える
# np.repeat(A,N)は配列A内の各要素をN回繰り返す
print(pairwise_tukeyhsd(data_arr,ind_arr))
上の関数を使って
4つの高校の配列をWXYZの4つのグループに分配し,多重比較してみます.
tukey_hsd(list('WXYZ') , W高校,X高校,Y高校,Z高校)
Multiple Comparison of Means - Tukey HSD,FWER=0.05
==============================================
group1 group2 meandiff lower upper reject
----------------------------------------------
W X -5.0 -15.2598 5.2598 False
W Y -0.5 -10.7598 9.7598 False
W Z -11.5 -21.7598 -1.2402 True
X Y 4.5 -5.7598 14.7598 False
X Z -6.5 -16.7598 3.7598 False
Y Z -11.0 -21.2598 -0.7402 True
----------------------------------------------
W高校とZ高校間,Y高校とZ高校間に得点の有意差がありました.
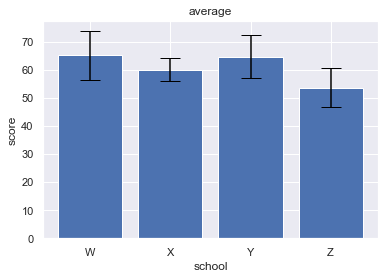
left = np.array(["W", "X", "Y", "Z"])
height = np.array(np.mean(tdata))
yerr = np.array(np.std(tdata))
plt.bar(left, height, yerr=yerr, ecolor="black", capsize=10)
plt.title("average")
plt.xlabel("school")
plt.ylabel("score")
(標準誤差のバー付けたかったけど時間かかりそうだったのでひとまず標準偏差にしてます)
まとめ
得点順は平均点で見ると
W校 > Y校 > X校 > Z校
の順で高かったです.また,W校とZ校の差及びY校とZ校の得点の開きは
統計的にみると偶然ではなくて,学校の違いが影響しているということが言えそうです.
なんてことを,Pythonで実行できました!
以上です.
拙い文章を最後まで読んでいただき,ありがとうございました.
終わりに
研究室の優秀な優秀な後輩,きなこめ君とたなけん君に感謝ですm(_ _)m