はじめに
データ分析の華といえば、観測データに潜む関係性を説明できるような統計モデルの構築ですね。統計モデルの構築には確率分布の理解がかかせません。
データ分析の考え方では、ある変数のデータは確率的な現象から発生しています。逆に言えば観測されたデータのパターンはどういった確率分布によって表現できるでしょうか?
最尤推定法
それには確率分布を当てはめてみるというのが一つの手です。といっても確率分布はパラメータしだいで形が変化するので、当てはめには観測データに基づいた適切なパラメータ値を決めてやる必要があります。そのパラメータ値を計算するメジャーな方法として、最尤推定法があります。
最尤推定法のやり方をざっと書きますと、得られたデータがあるパラメータθを持つ確率分布から抽出されたN個のデータYと仮定し、値一つ一つの抽出確率$p(y_i|θ)$をN個分かけあわせたもの尤度関数Lとします。
$$L(θ|{y_i}) = p(y_1|θ) × p(y_2|θ) × ··· × p(y_N|θ)=\prod_{i=1}^{N}p(y_N|θ)$$
尤度関数Lが最大になるようなパラメータ値を計算します。計算しやすい形に変換(対数化)しパラメータの数だけ偏微分して解析的に解くだけ・・・という流れです。
実際にやってみる
確率分布はデータによって離散型と連続型2つがありますが、今回は離散型の確率分布の例としてポアソン分布の最尤推定と確率分布の当てはめをやっています。
- 離散型確率分布:ポアソン分布(今回)
-
連続型確率分布:正規分布(次回)
離散型確率分布:ポアソン分布
ポアソン分布はカウントデータに主に用いられます。分布を表す確率関数は以下の通りです。
$$
P(y)=\frac{λ^ye^{-λ}}{y!}(λ=yの平均を表すパラメータ、y=0,1,2,3...)
$$
推定と分布の当てはめをするテストデータは答え合わせができるよう、あらかじめ対象の確率分布から作成しておきます。
"""ポアソン分布からの乱数 """
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(seed=10)
# パラメータλ=2.4
poisson_values = np.random.poisson(lam=2.4, size=1000)
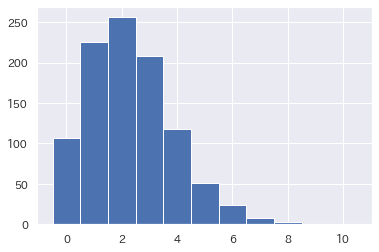
p_y, bin_edges, patches = plt.hist(poisson_values , bins=11, range=[-0.5, 10.5], normed=True)
y_k = 0.5*(bin_edges[1:] + bin_edges[:-1])
y_k #y
p_y #p(y)
得られた1000個の疑似データの値とその数が出ていますね。
さて、このようなデータに対し、ポアソン分布を当てはめそのパラメータを最尤推定してみます。
""" 対数尤度関数を偏微分してパラメータ推定 """
import sympy #代数計算するライブラリ(微分や方程式を解く)
# 変数を定義
sympy.var('λ y ')
# 尤度p(パラメータ|y)を定義
f = (λ**y)*sympy.exp(-λ)/sympy.factorial(y)
# 対数化
logf=sympy.log(f)
# fを偏微分して、式を展開
pdff = sympy.expand(sympy.diff(logf, λ))
対数尤度をパラメータλについて偏微分した式pdffが$\frac{y_i}{λ}-1$になっていますね。これをデータ分合計した$\sum_{i=1}^{1000}(\frac{y_i}{λ}-1)=0$になるλを求めてやればよいので
def L_sympy(f,var,values):
likelihood = 0 #尤度の初期値
for i in np.arange(len(values)): #データの個数分
# model output
# print(values[i])
likelihood += f.subs(var,values[i]) #yに値を代入
# print(likelihood)
param = sympy.solve(likelihood, λ) #λについての方程式を解く
# print(param)
return param
L_sympy(pdff,"y",poisson_values)
パラメータ推定量:[289/125]=2.312
パラメータλが2.312と推定されました。この疑似データのλの設定は2.4ですので、いい感じに推定できてますね。
パラメータ推定が複雑なケース
教科書的なやり方は上記の通り偏微分した式(導関数)を解けばパラメータを計算できる式を直接得ることができます。しかし、単純な1変数データへ確率分布の当てはめと異なり一般的な統計モデリングではリンク関数で変換した線形モデルを当てはめるため推定するパラメータが複数になり、式もより複雑なので簡単には解けません。
複雑な場合のパラメータ推定
そのため、非線形方程式を解く方法を使います。(いわゆる$\frac{y}{λ}-1$のような線形の式ではなく、$λ^2+θ^3+...$のような非線形)。
"""離散型確率分布の関数(確率質量関数)"""
def probability_poisson(y,λ):
from scipy.special import factorial
# λ: パラメータ
# y: データy:y回発生する
# return: データYの確率P(y|パラメータ)
return (λ**y)*np.exp(-λ)/factorial(y)
"""対数尤度関数:離散型"""
def L_func(param,y):
likelihood = 0 #尤度の初期値
for i in np.arange(len(y)):
# model output
p = probability_poisson(y[i], param)
# likelihood
likelihood += -np.log(p) #尤度
return likelihood
"""パラメータ推定"""
"""
準Newton法(BFGS,L-BFGS法:複雑な場合にメモリの節約などが可能)
"""
from scipy import optimize
x0 = [2] #パラメータの初期値
bound = [(0, None)] #最適パラメータ検索の範囲(min,max)
params_MLE = optimize.minimize(L_func,x0,args=(poisson_values),method='l-bfgs-b',
jac=None, bounds=bound, tol=None, callback=None,
options={'disp': None, 'maxls': 20, 'iprint': -1,
'gtol': 1e-05, 'eps': 1e-08, 'maxiter': 15000,
'ftol': 2.220446049250313e-09, 'maxcor': 10,
'maxfun': 15000})
# パラメータの最尤推定量
print('パラメータ:',params_MLE.x)
# パラメータ数
k=1
# AIC(一番小さい値がはてまりの良い確率分布)
print('AIC:',params_MLE.fun*(2)+2*k)
パラメータ: [2.31200054]
AIC: [3607.0081302]
同様にパラメータλが2.312と推定されました。
手っ取り早くパラメータを知りたい・・・
"""curve_fitでとりあえずパラメータ計算するのもあり"""
from scipy.optimize import curve_fit
parameters, cov_matrix = curve_fit(f=probability_poisson, xdata=y_k, ydata=p_y)
print("パラメータ:",parameters, "共分散:",cov_matrix)
パラメータ: [2.31643586] 共分散: [[0.00043928]]
データに当てはめて図示してみる
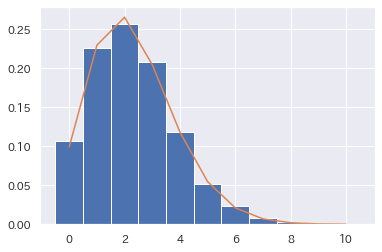
推定したパラメータλ=2.312として、確率分布(ポアソン分布)をデータに当てはめてみます。
"""当てはまっているかの図示"""
acc_mle = probability_poisson(y_k, params_MLE.x)
plt.hist(poisson_values , bins=11, range=[-0.5, 10.5], normed=True)
plt.plot(y_k,acc_mle)
良い感じですね。