単調性，強単調性，局所非飽和性

大学院レベルのミクロ経済学で多くの人が挫折する最初のポイントは，たぶん今回の記事の内容ではないかと思う．

消費者の振る舞いを選好に基づいて分析する上で，選好に対して何らかの仮定を置くことは客観的な分析をする上で当然必要なのだが，前回の記事 合理性を持つ選好と効用関数 では選好が合理性を持つという仮定を扱った．

今回は合理性とは別の視点で，「どういうバンドルがより望ましい（より選好される）のだろうか」という，望ましさに関する仮定を設ける上でよく使われる単調性や局所非飽和について論じる．

ここでは，選択肢集合を $X = \mathbb{R}^N_{+}$ と表す．バンドルは $\boldsymbol{x} \in X$ や $\boldsymbol{y} \in X$ や $\boldsymbol{z} \in X$ を使う．また，$\boldsymbol{x}$ の $k$ 番目の要素，すなわち第 $k$ 番目の商品の量を $x_k$ と表す．$y_k$，$z_k$ も同様である．

単調性と強単調性

ズバリ，選好が単調性（monotonicity）を持つ定義は以下の通り．

---

単調性（monotonicity）

$\forall \boldsymbol{x} \in X, \ \forall \boldsymbol{y} \in X$ について，

$ x_k \ge y_k \hspace{1em} \mathrm{for \ every} \ k \ \Rightarrow \ \boldsymbol{x} \succsim \boldsymbol{y}$

が成り立ち，また

$ x_k > y_k \hspace{1em} \mathrm{for \ every} \ k \ \Rightarrow \ \boldsymbol{x} \succ \boldsymbol{y}$

が成り立つとき選好は単調である．

---

単調性（後述する強単調性と比較して，弱単調性とも言う）は，要するに，一方のバンドルについてある幾つかの財の量が他方のバンドルより多くても，一つでも同じ量の財があるなら2つのバンドルは（弱い）選好 $ \succsim $ でしか比較できないというもの．厳密な選好 $ \succ $ を言いたければ，全部の財が他方のバンドルより多くないとダメというわけである．

具体的には $X=\left\{ガム，アメ，せんべい\right\}$ という選択肢集合のとき，$(2,2,1) \succsim (1,2,1)$ となり，ガムが1個だけ多くて他は右側のバンドルと同じ量である左側のバンドルの方が「弱く」選好されるというわけである．

単調性よりも強い仮定が以下の強単調性（strong monotonicity）である．

---

強単調性（strong monotonicity）
$\forall \boldsymbol{x} \in X, \ \forall \boldsymbol{y} \in X$　について，

$ \boldsymbol{x} \ne \boldsymbol{y} \ \land \ x_k \ge y_k \hspace{1em} \mathrm{for \ every} \ k \ \Rightarrow \ \boldsymbol{x} \succ \boldsymbol{y}$

が成り立つとき，選好は単調である．

---

要するに，強単調性のもとではバンドルの内1つの財の量でも一方のバンドルより多ければ，他の財が同じ量でも $\boldsymbol{x} \succ \boldsymbol{y}$ というわけである．

具体的には $X=\left\{ガム，アメ，せんべい\right\}$ という選択肢集合のとき，$(2,2,1) \succ (1,2,1)$ となり，ガムが1個だけ多くて他は右側のバンドルと同じ量である左側のバンドルの方が「強く」選好されるというわけである．

単調・強単調なる選好と効用関数

簡単に $N=2$ のケースで考えるが，（効用関数 $u(\cdot)$ が存在するとして）選好が単調であるならば以下が成り立つ．

u(\alpha x_1, x_2) \ge u(x_1, x_2) \ \land \ u(\alpha x_1, \alpha x_2) > u(x_1, x_2) \hspace{1em} \forall \alpha > 1

これは単調性の定義よりほぼ明らかだろう．つまり，一つでも財の量が同じ（上式の $\land$ の左側の式での $x_2$）なら（弱い）選好で繋がるので，効用水準の大小比較では$=$つき不等式となる．しかし，全部の財の量が上回る（上式の $\land$ の右側の式）ならば厳密な選好で繋がるので，$=$なしで厳密に効用水準が大きくなるわけである．

これより，選好が強単調であるならば以下が成り立つことは自明だろう．

u(\alpha x_1, x_2) > u(x_1, x_2)　\hspace{1em} \forall \alpha > 1

一般的に，$\mathrm{強単調} \Rightarrow \mathrm{単調}$ が成立する．（逆は必ずしも成り立つわけではない）

以下の副節で単調だが強単調ではない例，および強単調かつ単調な例を示す．

例1: 完全補完財を表す効用関数

完全補完財（perfect complements）は学部レベルの経済学でよく出てくるものだと思う．実際にバラバラに売ってるかどうか知らんが，「右足用の靴」と「左足用の靴」とは完全補完財の例である．つまり，「右足用の靴の量を一定に保ったまま，左足用の靴だけ大量に買っても効用は全く変化しない（嬉しくもないし悲しくもない）」わけで，両方が同じ比率で変化して初めて効用が変化するもの，というわけである．

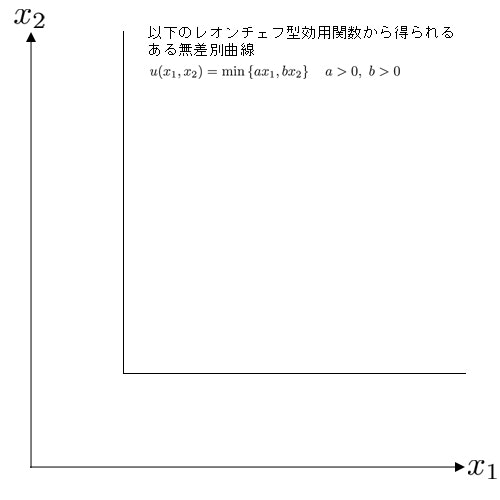
完全補完財を表すような効用関数の典型例として，以下のようなレオンチェフ型と呼ばれる効用関数がある．

u(x_1, x_2) = \min \left\{ ax_1, bx_2 \right\} \hspace{1em} a>0,\ b>0

この効用関数から得られる無差別曲線は，下図のようにL字型をしている．

このようなレオンチェフ型の効用関数が表す選好は，単調ではあるが強単調ではない．

何故なら，$\min \left\{ ax_1 + \delta, bx_2 \right\} \ (\delta >0)$ は，必ずしも $\min \left\{ ax_1, bx_2 \right\}$ より大きいわけではない．（例えば，$\min \left\{ ax_1, bx_2 \right\} = bx_2$ の場合，$ax_1$ にどんな正の値を足しても最小値は $bx_2$ のまま）よって，第1財を増やしても効用が厳密に大きくなるわけではない（第2財についても同様）ので，強単調性は満たさない．

一方，$\min \left\{ ax_1 + \delta, bx_2 + \delta \right\} > \min \left\{ ax_1, bx_2 \right\}$ なので，単調性は成立する．

例2: 完全代替材を表す効用関数

学部レベルでは完全補完財とセットで習うものが完全代替財（perfect substitutes）であろう．ビールがこの世から消えても，酎ハイがあればそのロス感を完全に埋められるような人にとっては，ビールと酎ハイは完全代替財の関係にある．つまり，ある商品を買うことで得られる効用を，他の商品を買うことで代替できるというわけである．

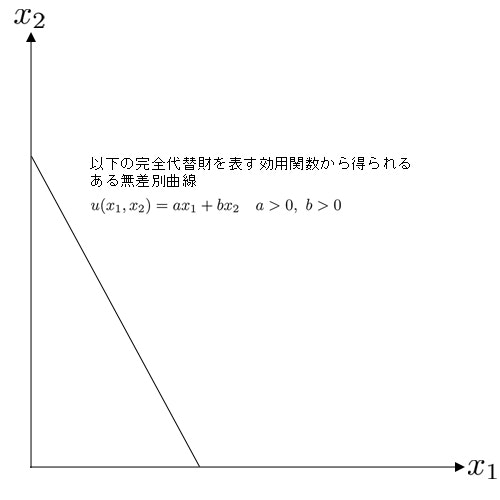
完全代替財を表すような効用関数の典型例は以下の式である．

u(x_1, x_2) = ax_1 + bx_2 \hspace{1em} a>0,\ b>0

この効用関数から得られる無差別曲線は，下図のような直線型をしている．

このような完全代替財を表す効用関数が表す選好は，$(ax_1 + \delta ) + bx_2 > ax_1 + bx_2$ なので強単調である．（もちろん単調でもある）

局所非飽和性

局所非飽和性について論じる前に，「局所」ではない一般的な非飽和性（nonsatiation）について述べる．

---

非飽和性（nonsatiation: NS）
$\forall \boldsymbol{x} \in X$　について，$\boldsymbol{x}$ とは異なるある $\boldsymbol{y} \in X$ があって，$\boldsymbol{y}$ が $\boldsymbol{x}$ より厳密に選好される（i.e. $\boldsymbol{y} \succ \boldsymbol{x}$）とき，選好が非飽和であるという．

---

非飽和性とは，要するに欲望には限りがないということを表している．つまり，どんな財バンドルに対しても，それよりも厳密に選好される別のバンドルが存在するというわけである．

例えば，タバコ10箱よりもタバコ30箱の方がより嬉しい（厳密に選好される）し，タバコ30箱よりもタバコ100箱の方がより嬉しいし，タバコ100箱よりも…（以下延々続く）というわけである．¹

このタバコのみの1次元のバンドルだとちょっとイメージしにくいが，単調性や強単調性のようにバンドルの各要素が大きい方がいいという条件を一切つけておらず，単に「いくらでも嬉しさを上げちゃうバンドルがあるよ」としか言っていないので，非常に弱い仮定であることが分かるだろう．

しかし，非飽和性は余りに大域的というか包括的過ぎて使いにくい．先のタバコの例で言えば，10箱のバンドルより嬉しいバンドルとして，10000000箱のバンドルを考えることもできるし，999999999999999箱のバンドルを考えてもいいわけである．つまり，とんでもなく「離れた」バンドルを考えてもいいというのが非飽和性なのだが，そんなデカい世界のことを言われても困るわけで，普通に分析するときには現在のバンドルの「近く」で非飽和なバンドルが存在することを仮定した方が何かと便利である．

解析的には，ある点の「近く」のものを考えるときには，その点を中心とした任意の半径の開球（2次元平面で言えば，その点を中心とした円周を除く円の内部）を考える．その開球内に，中心点のバンドルよりも嬉しいバンドルがあれば，まさに非飽和なバンドルが局所的に存在することを意味する．

よって，局所非飽和性（local nonsatiation）の定義は次のように書ける．

---

局所非飽和性（local nonsatiation: LNS）
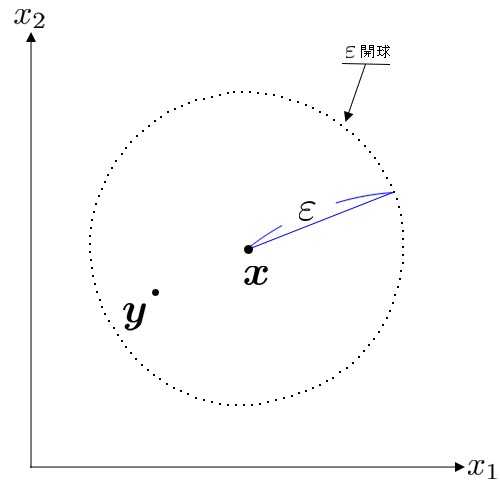
$\forall \boldsymbol{x} \in X$　について，$\boldsymbol{x}$ とは異なるある $\boldsymbol{y} \in X$ があって，$\boldsymbol{y}$ が $\boldsymbol{x}$ より厳密に選好され（i.e. $\boldsymbol{y} \succ \boldsymbol{x}$），かつ $\boldsymbol{y}$ が $\boldsymbol{x}$ から $\forall \varepsilon > 0$ ほど離れていない（i.e. $|| \boldsymbol{y} - \boldsymbol{x} || < \varepsilon $） とき，選好が局所非飽和であるという．

---

下図のように，中心 $\boldsymbol{x}$ の半径 $\varepsilon$ の開球（$\varepsilon$開球）内に，$\boldsymbol{x}$ よりも厳密に選好される別のバンドル　$\boldsymbol{y}$ が存在することが局所非飽和性である．

微分積分学で出鼻をくじかれることも多い「イプシロンデルタ論法」のイプシロンと同じで，このような局所性の議論における任意の正数 $\varepsilon$ の「真意」は，「0.01でも0.00000001でも，（正数なので0にはならないが0に限りなく近づけて）いくらでも開球の半径を小さくできる」ということである．つまり，「どんなバンドル $\boldsymbol{x}$ でも，そのいくらでも近くのところに，必ず $\boldsymbol{x}$ よりも嬉しくなる別のバンドルがある」というのが局所非飽和性の真意である．

局所非飽和と無差別曲線

局所非飽和を仮定すると，無差別曲線は絶対に「厚み」を持たない（つまり無差別"領域"にならない）ことが保証される．これは局所非飽和性を持つ選好の重要な特徴の一つである．

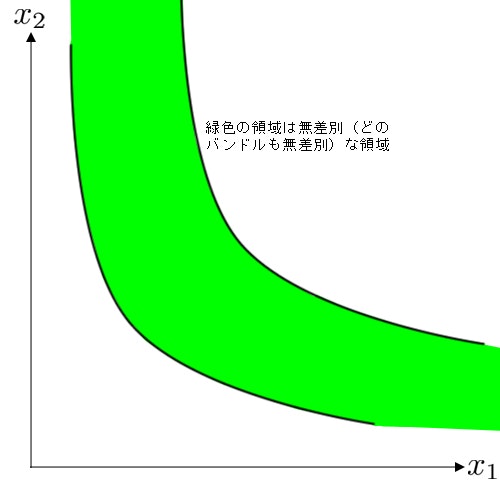
例えば，下図のような「厚み」のある無差別曲線（無差別領域）を考えてみる．

もし，選好が局所非飽和性を満たすならば，下図のように，全てのバンドルが無差別であるはずのこの緑色の領域中に，無差別でないバンドル（より厳密に選好されるバンドル）を見出すことができてしまう．

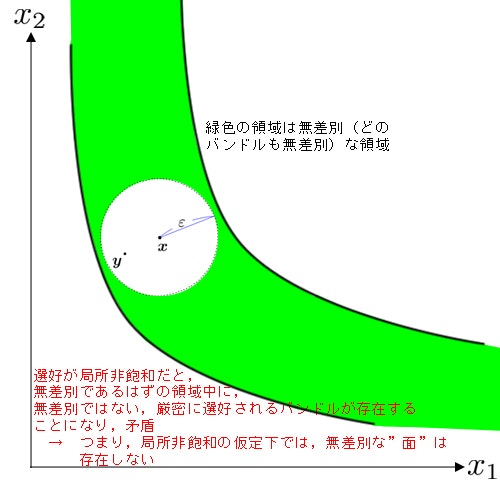
従って，局所非飽和な選好のもとでは，その選好が表す効用関数から得られる無差別曲線は，決して「厚み」を持たない（つまり面ではなく線になる）ことが言える．

強単調性・単調性・局所非飽和性

局所非飽和性は単調性よりも弱い仮定であり，$\mathrm{単調} \Rightarrow \mathrm{局所非飽和}$ が成立する．（逆は必ずしも成り立つわけではない）

従って，$\mathrm{強単調} \Rightarrow \mathrm{単調} \Rightarrow \mathrm{局所非飽和}$ が成立する．

参考文献

1. Munoz-Garcia, F. (2017) Advanced Microeconomic Theory: An Intuitive Approach with Examples. The MIT Press, ISBN: 978-0262035446.
2. Mas-Colell, A., Whinston M.D., and Green, J.R. (1995) Microeconomic Theory. Oxford University Press, ISBN: 978-0195102680.

関連記事

• ミクロ経済学（大学院レベル）の目次

1. 「非飽和」という言葉がやや分かりにくいが，「決して飽きない」という言葉に置き換えれば意味が分かるだろう． ↩