はじめに
前々回の記事では,出先のノート PC でささっとシミュレーションプログラムを作成しました。わざわざ Visual Studio 等をインストールするのも面倒ですから,Windows に内蔵されている .NET Framework の C# コンパイラを使用しました。乱数も備え付けの System.Random() クラスを用いました。つまり,Donald E. Knuth の減算乱数ジェネレーターアルゴリズムを用いたことになります。
たまたま上手くいったものの,もしも他の乱数エンジンを採用していたら,どうなっていたのでしょうか?
言語の選択
さまざまな乱数エンジンが標準ライブラリとして用意されているということで C++ を選びました。正直 C++ は苦手な言語なのですが,今回のプログラムの長さくらいであれば何とかなるでしょう。
ソースコード(C++)
ソースコードは大半が重複しているので,差分を目立たせるため diff 形式で表示しています。利用する場合には手作業で行頭のプラス(+)やマイナス(-)記号を削除して下さい。
線形合同法の場合
C言語の標準ライブラリにある rand() でも採用されている線形合同法です。C++ には minstd_rand0 と minstd_rand の二種類が用意されており,後者のほうが改善されたパラメータとのことなので採用しました。
#include <iostream>
#include <random>
const int MAX_LOOP = 1000*1000*1000;
const int MAX_HIST = 1000;
int main() {
int hist[MAX_HIST] = { 0 };
+ std::minstd_rand rand(0);
for(int i = 0; i < MAX_LOOP; i++) {
for(int n = 0, flag = 0; n < MAX_HIST; n++) {
int x = rand() % 30;
if((flag |= (1 << x)) == 0x3FFFFFFF) {
hist[n]++;
goto BREAK;
}
}
std::cerr << "TABLE OVERFLOW ERROR!!" << std::endl;
return -1;
BREAK:;
}
for(int i = 0; i < MAX_HIST; i++)
std::cout << i + 1 << "\t" << (double)hist[i] / MAX_LOOP << std::endl;
return 0;
}
リオーダーアルゴリズム(Knuth-B)の場合
Knuth のリオーダーアルゴリズム B と呼ばれるものです。
#include <iostream>
#include <random>
const int MAX_LOOP = 1000*1000*1000;
const int MAX_HIST = 1000;
int main() {
int hist[MAX_HIST] = { 0 };
+ std::knuth_b rand(0);
for(int i = 0; i < MAX_LOOP; i++) {
for(int n = 0, flag = 0; n < MAX_HIST; n++) {
int x = rand() % 30;
if((flag |= (1 << x)) == 0x3FFFFFFF) {
hist[n]++;
goto BREAK;
}
}
std::cerr << "TABLE OVERFLOW ERROR!!" << std::endl;
return -1;
BREAK:;
}
for(int i = 0; i < MAX_HIST; i++)
std::cout << i + 1 << "\t" << (double)hist[i] / MAX_LOOP << std::endl;
return 0;
}
メルセンヌツイスターの場合
業界最強とも呼ばれるメルセンヌツイスターが標準で用意されているというのが素晴らしいですね。なお,64bit 版の mt19937_64 も用意されています。ただ,実際に比較してみると 64bit マシンなのに何故か mt19937 のほうが僅かに速かったのでコチラの結果を用いました。
ここで言う 64bit 版の mt19937_64 とはあくまで 64bit 整数の乱数列を生成するという意味です。一方,32bit 版の mt19937 は 32bit 整数の乱数列を生成します。この記事を書いた当時,mt19937_64 は mt19937 と同じ乱数列を生成し,かつ 64bit プロセッサ向けに最適化された高速アルゴリズムを採用したものと勘違いしていました。2024年10月29日追記
#include <iostream>
#include <random>
const int MAX_LOOP = 1000*1000*1000;
const int MAX_HIST = 1000;
int main() {
int hist[MAX_HIST] = { 0 };
+ std::mt19937 rand(0);
for(int i = 0; i < MAX_LOOP; i++) {
for(int n = 0, flag = 0; n < MAX_HIST; n++) {
int x = rand() % 30;
if((flag |= (1 << x)) == 0x3FFFFFFF) {
hist[n]++;
goto BREAK;
}
}
std::cerr << "TABLE OVERFLOW ERROR!!" << std::endl;
return -1;
BREAK:;
}
for(int i = 0; i < MAX_HIST; i++)
std::cout << i + 1 << "\t" << (double)hist[i] / MAX_LOOP << std::endl;
return 0;
}
XorShiftの場合
流石に XorShift は用意されていませんでしたが,とても簡単なので自作しました。パラメータは wikipedia にあるものを採用しました。乱数の種は 0 以外の値を入れる必要があります。デフォルトは 1 としています。
#include <iostream>
-#include <random>
+class XorShift {
+private:
+ uint64_t x = 1;
+public:
+ XorShift() {}
+ XorShift(uint64_t s) {x = s;}
+ int operator()() {
+ x ^= x << 13;
+ x ^= x >> 7;
+ x ^= x << 17;
+ return (int)(x & 0x7FFFFFFF);
+ }
+};
const int MAX_LOOP = 1000*1000*1000;
const int MAX_HIST = 1000;
int main() {
int hist[MAX_HIST] = { 0 };
+ XorShift rand(1);
for(int i = 0; i < MAX_LOOP; i++) {
for(int n = 0, flag = 0; n < MAX_HIST; n++) {
int x = rand() % 30;
if((flag |= (1 << x)) == 0x3FFFFFFF) {
hist[n]++;
goto BREAK;
}
}
std::cerr << "TABLE OVERFLOW ERROR!!" << std::endl;
return -1;
BREAK:;
}
for(int i = 0; i < MAX_HIST; i++)
std::cout << i + 1 << "\t" << (double)hist[i] / MAX_LOOP << std::endl;
return 0;
}
計算時間の比較
4つのアルゴリズムの計算時間を比較しました。プログラムの中身は御覧の通りスカスカなので,乱数の計算時間が大半を占めると考えて良いでしょう。
Knuth-B は線形合同法よりも2~3倍遅いと言われており,それを立証した結果となりました。XorShift が最速なのは納得です。メルセンヌツイスターは思っていたより速くて驚きました。
コンパイラは Clang 17.0.3 です。Visual Studio 2022 Community Edition のインストーラーでインストールしたものです。ThinkPad X280 で計測しました。
乱数の品質
さて,本題の乱数の品質です。まず,線形合同法の結果を示します。グラフ全体を見るとさほど不自然ではありませんが,よく見ると微小な凸凹に気づきます。
乱数の品質を比較するため,前回の記事で求めた値を理想値として,その比をグラフにしてみました。線形合同法だけが突出して粗いことが分かりますね。それ以外のアルゴリズムは,少なくとも今回のシミュレーションでは大した差異がないように見えます。
線形合同法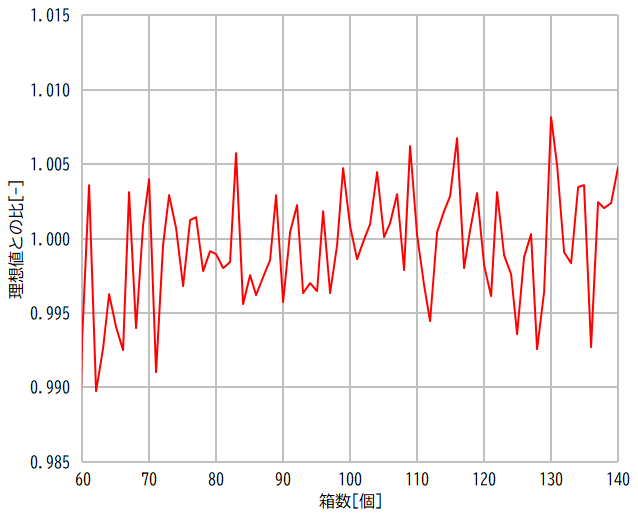
|
Knuth-B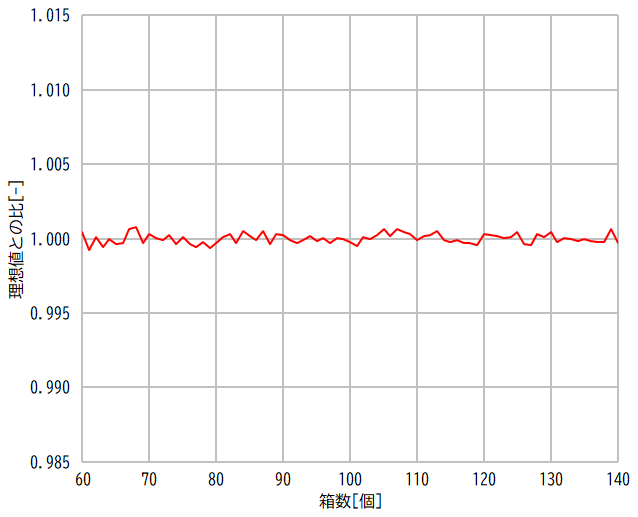
|
|---|---|
XorShift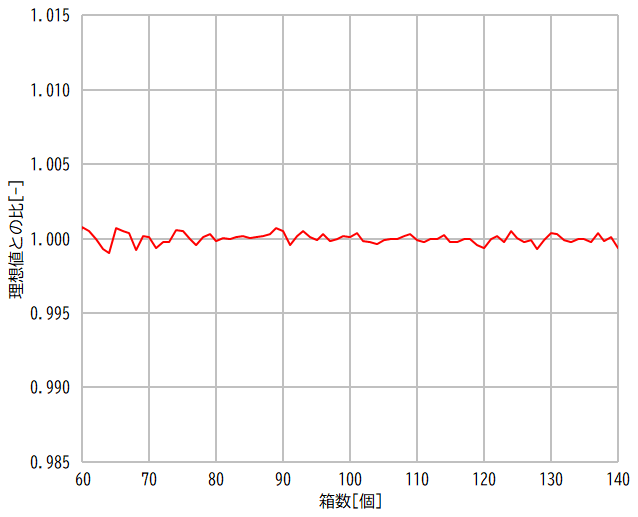
|
メルセンヌツイスター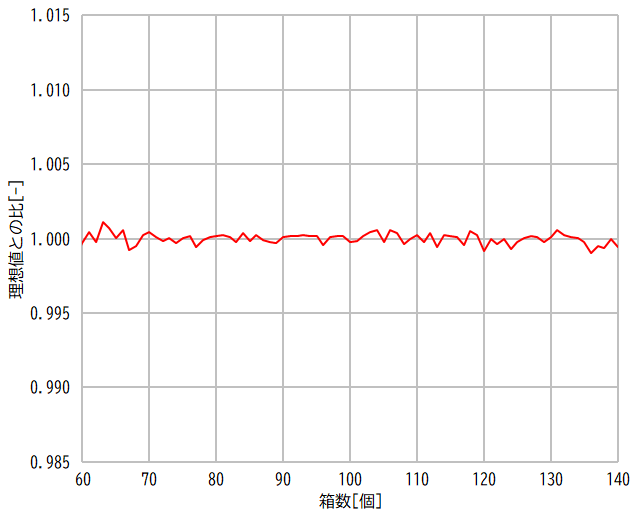
|
最頻値・中央値・平均値を比較してみると,線形合同法が突出して悪いことが分かります。それ以外のアルゴリズムにはあまり差が無いように見えますが,敢えて優劣をつけるなら平均値の僅かな差異に着目して,メルセンヌツイスターが最善,XorShift が次善,Knuth-B が僅差で続くといった感じでしょうか。
| アルゴリズム | 最頻値 | 中央値 | 平均値 |
|---|---|---|---|
| 線形合同法 | 104 | 113 | 119.874757 |
| Knuth-B | 102 | 113 | 119.848911 |
| XorShift | 102 | 113 | 119.849069 |
| メルセンヌツイスター | 102 | 113 | 119.849563 |
| 理想値 | 102 | 113 | 119.849614 |
まとめ
既に有るものを使うのであれば,品質とスピードを兼ね備えたメルセンヌツイスターが良いという当たり前の結論になりました。
スピードを要求する用途であれば,XorShift も悪くない選択ですね。シンプルなので実装は容易ですし。
おまけ
前々回の記事での C# 版プログラムの乱数ですが,実は品質があまり良くなかったのです。何故か 68 箱のところで突然飛び出ているのです。
最頻値・中央値・平均値を比較してみても C++ 版の大半に劣ることが分かります。
| 言語 | アルゴリズム | 最頻値 | 中央値 | 平均値 |
|---|---|---|---|---|
| C++ | 線形合同法 | 104 | 113 | 119.874757 |
| Knuth-B | 102 | 113 | 119.848911 | |
| XorShift | 102 | 113 | 119.849069 | |
| メルセンヌツイスター | 102 | 113 | 119.849563 | |
| C# | 減算乱数ジェネレータ | 101 | 113 | 119.843263 |
| 理想値 | 102 | 113 | 119.849614 | |
同じ Knuth 本に掲載されているアルゴリズムとはいえ大きな差があります。実は本記事を書き始めた当初 C++日本語リファレンスの std::knuth_b の頁には
このアルゴリズムは、Microsoft .NET FrameworkのSystem.Randomクラスにも、実装として使用されている。
との記載があったのですが,両者のソースコードを手に入れて比較したり(C++ のほうはテンプレートだらけで苦労した),実際に Knuth 本を図書館で借りて読んでみるとどうやら両社は別物ではないかと思うようになりました。
.NET Framework の System.Random クラスで採用されているのは Knuth 本でいうアルゴリズム A(加算式乱数発生器)であり,Microsoft は実装するにあたり減算式に変更する等細部を変更していますが,原理的にはアルゴリズム A と同じものだと思います。一方,C++ の std::Knuth_b のほうは Knuth 本でいうアルゴリズム B(シャッフルによるランダム化)でしょう。この件に関して質問したところ,翌日には修正されていました。素早い対応に感謝します。
前回の記事から投稿間隔が開いてしまったのはその事実確認のためです。