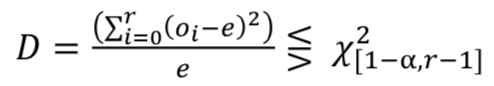乱数の仕組み

プログラミングにおいて乱数を生成するとき、コンピュータはどのような仕組みで乱数を生成するのか。
コンピューターは無作為な動作を作ることはできないので、あるアルゴリズムに従ってランダムな数を決めています。
生成される数はアルゴリズムに依存するので、コンピュータは真の乱数を得ることができません。
このあるアルゴリズムによって決められたランダムに見える数を擬似乱数といいます。

擬似乱数

乱数列のように見えるが、実際には確定的な計算によって求めている擬似乱数列による乱数
擬似乱数-Wikipedia

擬似乱数の性質

• 無相関シーケンス - 乱数のシーケンスは連続的に無相関である。
• 長周期 - 乱数生成器は長周期である（理想的には、生成器は繰り返してはいけなく、繰り返しは非常に大きな乱数のセットの生成後にのみ行われる）。
• 一様性 - 乱数の並びは一様で偏りが無い。 つまり、乱数の出現する割合は等しくなければならない。
• 効率 - 乱数生成器は効率的である。

乱数の周期

乱数生成器には、乱数の周期があり、過去に現れた数と同じ数が現れればループとなり、その長さが周期となる。
ほとんどの乱数生成器は、基本的に疑似乱数(整数)の周期を持っています。

周期の性質

• 有限個の整数を持つ。
• 整数は特定の順序で進む。
• 周期を超えた場合、繰り返される。
• 整数は区別されない。つまり、同じ数を繰り返すかもしれない。

擬似乱数生成アルゴリズム

1. 線形合同法

• 線形合同法とは、1951年にD.Lehmerによって導入された、擬似乱数生成のアルゴリズムとして最もよく知られている方法です。
  この方法では、乱数 𝑥1、𝑥2、... は式 𝑥(𝑖+1) = (𝐴×𝑥𝑖) mod 𝑀 によって生成されます。

• 𝑥0 はシードと呼ばれ、計算の際、初期状態として設定する値です。
  シード値を同じ値にすることで、毎回同じ擬似乱数を生成できます。
  ※ 𝑥0は0以外の値。0にすると擬似乱数が全て0になってしまう。

• 𝑥𝑖の値に対応する数が𝑟𝑖 = 𝑥𝑖 / 𝑀で生成されます。

• 𝑟𝑖の範囲は、0≦𝑟𝑖≦1になり、任意の𝑟𝑖は他の任意の𝑟𝑖の出現確率と等しく、平均は0.5 に非常に近くなります。

• AとMが正しく選択された場合、0<𝑥0<𝑀の任意の𝑥0も同様に有効です。もし𝑀が素数であれば、𝑥𝑖は1≤𝑥𝑖≤𝑀-1になります。

• 例えば、𝑀=11、𝐴=6、𝑥0=1の場合、数列は次のようになります。
  6,3,7,9,10,5,8,4,2,1,6,3,7,9,10,5,8, ...
  6から1までの10桁 = M-1の周期
  𝐴=5を選択した場合、5,3,4,9,1,5,3,4,9,1,5、...となり、M-1の周期を満たしません。

• 𝑀が素数なら、𝑀−1の全周期を与える𝐴が常に存在します。𝑀が大きければ、例えば31ビット素数であれば、ほとんど𝑀−1の全周期を満たします。

• Lehmerは、素数として𝑀 = 2^31-1 = 2147483647を提案しました。
  この素数では、𝐴=48271が𝑀−1の全周期を与える値の1つです。

• 𝑥0 = 1

• 𝑥(𝑖+1) = (48271 × 𝑥𝑖) mod (2^31 − 1)

擬似コード

def lcg(x0):
    x = x0  # x0はシード
    A = 48271
    M = 2147483647
    rand_seq = []  # 空のリスト(n個の擬似乱数を格納する)
    for i = 1 to n:
        x = (Ax) % M
        rand_seq.append(x)
    return rand_seq

• 実際には、上の擬似コードは殆どのコンピュータで上手く機能しません。
  問題は、（𝐴×𝑥）がオーバーフローする可能性があることです。(言語などによってデータ型には、とりうる値の範囲がある [int型　範囲 - Google 検索])
  オーバーフローが発生すると、（𝐴×𝑥）は（𝐴×𝑥）％2^𝑏(𝑏: コンピューターのint型変数のビット数)の値になります。

• これは、（𝐴×𝑥）がオーバーフローすると、（𝐴×𝑥）％𝑀が（（𝐴×𝑥）％2^𝑏）％𝑀）になることを意味します。 生成された配列の結果が代わり、その結果、配列の疑似乱数性に影響を与えます。

• 𝑀=2^𝑏 とすると、オーバーフローは（𝐴×𝑥）％𝑀の演算になります。

• そのため実際には、多くの生成器は𝑥(𝑖+ 1) = (𝐴×𝑥𝑖+𝐶) mod 2^𝑏に基づいています。

• ここで、上記の式に基づいて32ビット整数の乱数を生成するためのアルゴリズムを考えます。

• 32ビット整数の場合、符号に1ビットが使用され、整数の絶対値に他の31ビットが使用されるため、表現できる最大の整数は2^31 - 1 = 2147483647です。

• 𝑏 = 31、𝑀=2^𝑏として、𝑀は32ビット整数で表現できないので（𝑀 - 1）+ 1となるように実装します。以上を考慮すると、擬似コードは下のようになります。

擬似コード

def lcg(n):  # n - 生成する擬似乱数の数
    x = 53402397  # シード
    rand_seq = []  # 空のリスト(n個の擬似乱数を格納する)
    for i = 1 to n:
        x = 65539x + 125654
        if x < 0:  # オーバーフローチェック
            x += 2147483647  # +(M-1)
            x += 1
        rand_seq.append(x)
    return rand_seq

• しかし、上の擬似コードでは、まだ問題があります。𝑐が奇数の場合、𝑥𝑖の値は偶数と奇数で交互になり、𝑐が偶数の場合、𝑥𝑖の値はすべて偶数になってしまいます。

• 𝑥(𝑖+ 1) = (𝐴×𝑥𝑖+𝐶) mod 2^𝑏ではなく、𝑥(𝑖+1) = (𝐴×𝑥𝑖) mod 𝑀のままで、オーバーフロー問題を解決する他の方法を考えてみます。

• 𝑄 = 𝑀/𝐴、𝑅 = 𝑀%𝐴とすると、
  𝑥(𝑖+1) = (𝐴×𝑥𝑖) mod 𝑀は、
  𝑥(𝑖+1) = 𝐴(𝑥𝑖%𝑄) − 𝑅(𝑥𝑖/𝑄) + 𝑀((𝑥𝑖/𝑄) - (𝐴𝑥𝑖/𝑀))となります。

• 𝐴(𝑥𝑖％𝑄) − 𝑅（𝑥𝑖/𝑄） < 0のとき、（（𝑥𝑖/𝑄） - （𝐴𝑥𝑖/𝑀））は0か1で、（（𝑥𝑖/𝑄） - （𝐴𝑥𝑖/𝑀））は1です。

• したがって、𝑥(𝑖+1)は次のように計算できます。

1. 最初にy = 𝐴(𝑥𝑖%𝑄) − 𝑅(𝑥𝑖/𝑄)を計算します。
2. もし𝑦 ≥ 0なら𝑥(𝑖+1) = 𝑦、そうでなければ𝑥(𝑖+1) = 𝑦 + 𝑀になります。

• 最終的に、オーバーフローなしのアルゴリズムは以下のようになります。

擬似コード

def lcg(n):  # n - 生成する擬似乱数の数
    x = 1  # シード
    A = 48271
    M = 2147483647
    Q = M / A
    R = M % A
    rand_seq = []  # 空のリスト(n個の擬似乱数を格納する)
    for i = 1 to n:
        x = A(x % Q) - R(x / Q)
        if x < 0:
            x += M
        rand_seq.append(x)
    return rand_seq

2. 減算乱数ジェネレーターアルゴリズム

• 次は、Donald E. Knuthによって提案された減算乱数ジェネレーターアルゴリズム(subtractive random number generator algorithm)です。

• まず、配列を𝑥0,𝑥1,...,𝑥54で初期化します。
  このとき、線形合同法のアルゴリズムを使います。𝑥0, 𝑥1, ... , 𝑥54 = lcg(55)

擬似コード

def srng(n):  # n - 生成する擬似乱数の数
    x = 1
    next = 0
    A = lcg(55)
    rand_seq = Ø  # 空のリスト(n個の擬似乱数を格納する)
    for i = 1 to n:
        j = (next + 31) % 55
        x = A[j] - A[next]
        if x < 0:
            x += 2147483647
            x += 1
        A[next] = x
        next = (next + 1) % 55
        rand_seq.append(x)
    return rand_seq

• Mは大きな値でなければなりません。Mを10または2の累乗にすると使いやすい値になります。

• Aは大きすぎても小さすぎてもいけません。
  安全な選択は、Mより1桁小さい数字を使かうことです。
  Aは、特定のパターンを持たない任意の定数でなければなりません。

ランダム性のテスト

• 擬似乱数列と真の乱数列との様々な特性の関連性を判断するために多くのテストが開発されています。

• テストの一つとして、統計的検定法である𝜒2（カイ二乗）検定があり、実装は非常に簡単です。

• これは、生成された数値が合理的に拡散されているかどうかを確認するためのテストです。

• 𝜒2（カイ二乗）検定:

• 𝑜𝑖は値𝑖の発生頻度であり、 𝑒=𝑁/𝑟は予期される頻度です。

• 𝐷 = 0の場合、近似があります。

• 𝐷 ≤ 𝜒^2[1−α,𝑟−1] の場合、テストは信頼度αで合格となります。

例:

• 𝑥𝑖 = (125𝑥(𝑖−1) + 1) mod (2^12)

• 𝑥0 = 1で乱数の数は1000個

• 𝜒^2[0.9,9] = 14.68

• D = 10.38

• D(=10.38) ≤ 𝜒^2[0.9,9](=14.68)

Cell	Observd	Exptd	(𝑜−𝑒)^2/𝑒
1	100	100.0	0.000
2	96	100.0	0.160
3	98	100.0	0.040
4	85	100.0	2.225
5	105	100.0	0.250
6	93	100.0	0.250
7	97	100.0	0.490
8	125	100.0	6.250
9	107	100.0	0.490
10	94	100.0	0.360
Total	1000	1000.0	10.380

コンピュータにおける乱数

• 乱数は、多くの暗号アプリケーションの基礎です。

• 乱数を生成するための信頼できる「独立した」関数はありません。

• 今日のコンピュータでは、擬似乱数生成器（PRNG）によって生成された擬似乱数を使用して、乱数を近似することしかできません。