2018年度将棋A級順位戦で11名全員が5勝5敗の指し分けになる確率を考える

はじめに

2018年度の将棋A級順位戦はいろいろ異例であった。一つは例年10名で行われるリーグ戦が前年度に起きた事件の影響で11名で行われたこと，もう一つは６勝４敗の成績で６名が並び，名人挑戦をかけてこの６名によるプレーオフが行われたことである。ちなみに羽生善治竜王（当時）がこのプレーオフを勝ち抜いて佐藤天彦名人（当時）に挑戦した。

一方，降級のほうは同成績であってもプレーオフは行われず，順位によって降級者が決まる。

さて奇数人数の場合，とても低い確率だが全員が指し分けになる可能性がある。この場合，名人挑戦をかけて全員でプレーオフを行うことになる。一方，降級者は順位だけでは決められない。順位下位者でもプレーオフを勝ち抜いて名人挑戦者になった場合は降級を免れることができるからだ。

さて，11名の総当たりリーグ戦で11名全員が５勝５敗の指し分けになる確率はどれくらいだろうか？単純のため，全員の実力は互角とする。

2018年度A級順位戦結果

	稲 葉	羽 生	渡 辺	広 瀬	行 方	屋 敷	深 浦	佐 藤	久 保	豊 島	三 浦	勝	敗
稲葉陽八段	－	○	×	×	○	○	○	×	○	×	○	６	４
羽生善治竜王	×	－	○	○	×	○	○	×	○	×	○	６	４
渡辺明棋王	○	×	－	×	○	×	×	○	×	○	×	４	６
広瀬章人八段	○	×	○	－	○	×	○	×	×	○	○	６	４
行方尚史八段	×	○	×	×	－	○	×	○	×	×	×	３	７
屋敷伸之九段	×	×	○	○	×	－	×	×	×	×	×	２	８
深浦康市九段	×	×	○	×	○	○	－	×	○	×	○	５	５
佐藤康光九段	○	○	×	○	×	○	○	－	○	×	×	６	４
久保利明王将	×	×	○	○	○	○	×	×	－	○	○	６	４
豊島将之八段	○	○	×	×	○	○	○	○	×	－	×	６	４
三浦弘行九段	×	×	○	×	○	○	×	○	×	○	－	５	５

いきなり大人数で始めても問題の難しさがよく分からないので，手始めに少人数のリーグ戦から試してみる。

３人の場合を考える

リーグ表のうち対角項を除く上三角のマス目の数（３個）だけ自由度がある。すなわち全ての勝敗パターンは $2^3=8$ 個存在する。

	あ	い	う
あ	－
い		－
う			－

このうち三人とも１勝１敗となるパターンは下記の２つしかない。よって確率は $2/2^3 = 1/4$ となる。

	あ	い	う
あ	－	○	×
い	×	－	○
う	○	×	－

	あ	い	う
あ	－	×	○
い	○	－	×
う	×	○	－

誤った考え方
あ が２勝，あるいは２敗の確率はそれぞれ $(1/2)^2 = 1/4$ である。１勝１敗の指し分けになる確率は $1/2$ である。よって三人とも指し分けになる確率は $(1/2)^3 = 1/8$ とはならない。なぜなら あ の勝敗は いう の勝敗ともリンクしており，独立事象ではないからである。

５人の場合を考える

リーグ表のうち対角項を除く上三角のマス目の数（10個）だけ自由度がある。すなわち$2^{10}$ パターン存在する。

	あ	い	う	え	お
あ	－
い		－
う			－
え				－
お					－

このうち あ が いう に勝ち，えお に負けた場合を考える。これは あ が指し分けになる６パターンのうちの１つである。

	あ	い	う	え	お
あ	－	○	○	×	×
い	×	－
う	×		－
え	○			－
お	○				－

い が指し分けになるためには うえお に２勝１敗とならなくてはならないが，それは３パターンある。このうち い が う に負けて えお に勝った場合，うえお の三名はお互いに１勝１敗の指し分けにならなくてはならないが，そのようなパターンは２つある。$a = \lbrace ○, × \rbrace$ とし，$\bar{a}$ は $a$ の否定である。

	あ	い	う	え	お
あ	－	○	○	×	×
い	×	－	×	○	○
う	×	○	－	$a$	$\bar{a}$
え	○	×	$\bar{a}$	－	$a$
お	○	×	$a$	$\bar{a}$	－

一方，い が う に勝った場合は２パターンあるが，う は えお に対して２勝しなくてはならないので，い の勝敗を決めると えお の勝敗も一意に定まる。

	あ	い	う	え	お
あ	－	○	○	×	×
い	×	－	○	$a$	$\bar{a}$
う	×	×	－	○	○
え	○	$\bar{a}$	×	－	$a$
お	○	$a$	×	$\bar{a}$	－

以上より，５名全員が指し分けになるパターンは $6 \times (2 + 2) = 24$ となり，確率は $24/2^{10}=0.0234375$ となる。

７人の場合を考える

リーグ表のうち対角項を除く上三角のマス目の数（21個）だけ自由度がある。すなわち$2^{10}$ パターン存在する。

	あ	い	う	え	お	か	き
あ	－
い		－
う			－
え				－
お					－
か						－
き							－

もはや手計算で負えるレベルではないので，下記の C# プログラムを組んで計算したところ，確率は $2640/2^{21}=0.00125885$ となった。ちなみに計算時間は数秒で終わる。

7人のリーグで全員が指し分けになる確率を求める

bool[,]	map = new bool[7, 7];			// リーグ表
int[]	win = new int[7];				// 勝ち数
long	loop = 1L << 21;				// 総パターン数
int		count = 0;						// 全員指し分けのパターン数
for( long k = 0; k < loop; k++ ) {
	for( int i = 0; i < 7; i++ )		// リーグ表の初期化
		for( int j = 0; j < 7; j++ )
			map[i, j] = false;
	for( int i = 0; i < 7; i++ )		// 勝ち数の初期化
		win[i] = 0;
	long	mask = 1;					// リーグ表を埋める
	for( int i = 0; i < 6; i++ ) {
		for( int j = i + 1; j < 7; j++ ) {
			bool	flag = ( k & mask ) != 0 ? true : false;
			map[i, j] = flag;
			map[j, i] = !flag;
			mask <<= 1;
		}
	}
	int	n = 0;							// 勝ち数を数える
	for( int i = 0; i < 7; i++ ) {
		for( int j = 0; j < 7; j++ )
			if( map[i, j] ) win[i]++;
		if( win[i] == 3 ) n++;
	}
	if( n == 7 ) count++;
}
Console.WriteLine( "{0}/{1}={2}", count, loop, (double)count / loop );

９人の場合を考える

リーグ表のうち対角項を除く上三角のマス目の数（36個）だけ自由度がある。すなわち $2^{36}$ パターン存在する。７人の場合のプログラムをそのまま９人に拡張して実行させたところ，確率は $3230080 / 2^{36} = 4.70038503408432\times10^{-5}$ となった。ただし，計算に８時間かかった。これでは最終目標の11名の計算は現実的ではない。

このため あ が いうえお に勝ち，かきくけ に負けた場合という条件下で，残り８人が指し分けになるパターン数を求めることにした。

	あ	い	う	え	お	か	き	く	け
あ	－	○	○	○	○	×	×	×	×
い	×	－
う	×		－
え	×			－
お	×				－
か	○					－
き	○						－
く	○							－
け	○								－

下記の C# プログラムを組んで計算したところ，パターン数は 46144 となった。あ が指し分けになるパターンは ${}_8\textrm{C}_4 = 70$ なので，確率は

$46144 \times 70 / 2^{36} = 3230080 / 68719476736 = 4.70039\times10^{-5}$

となる。計算時間は２分弱となった。

9人のリーグの場合（Aが4勝4敗の指し分けという条件下での計算）

bool[,]	map = new bool[9, 9];			// リーグ表
int[]	win = new int[9];				// 勝ち数
long	loop = 1L << 36;				// 総パターン数
int		count = 0;						// 全員指し分けのパターン数
for( long k = 0x0F; k < loop; k += 0x100 ) {
	for( int i = 0; i < 9; i++ )		// リーグ表の初期化
		for( int j = 0; j < 9; j++ )
			map[i, j] = false;
	for( int i = 0; i < 9; i++ )		// 勝ち数の初期化
		win[i] = 0;
	long	mask = 1;					// リーグ表を埋める
	for( int i = 0; i < 8; i++ ) {
		for( int j = i + 1; j < 9; j++ ) {
			bool	flag = ( k & mask ) != 0 ? true : false;
			map[i, j] = flag;
			map[j, i] = !flag;
			mask <<= 1;
    	}
	}
	int		n = 0;						// 勝ち数を数える
	for( int i = 0; i < 9; i++ ) {
		for( int j = 0; j < 9; j++ )
			if( map[i, j] ) win[i]++;
		if( win[i] == 4 ) n++;
	}
	if( n == 9 ) count++;
}
Console.WriteLine( count );

11名の場合を考える

リーグ表のうち対角項を除く上三角のマス目の数（55個）だけ自由度がある。すなわち $2^{55}$ パターン存在するが，これをそのまま計算することは現実的ではない。

あ が いうえおか に勝ち，きくけこさ に負けた場合という条件下で，残り10人が指し分けになるパターン数を求めるとしても探索パターンは $2^{45}$ もあり，これでも現実的ではない。

	あ	い	う	え	お	か	き	く	け	こ	さ
あ	－	○	○	○	○	○	×	×	×	×	×
い	×	－
う	×		－
え	×			－
お	×				－
か	×					－
き	○						－
く	○							－
け	○								－
こ	○									－
さ	○										－

計算アルゴリズムを考え直す

そもそも全てのパターンを列挙して，その中から指し分けになるパターンをカウントする方法が非効率的なのだ。

たとえば あ が指し分けになるパターン数は ${}_{10}\textrm{C}_5 = 252$ 個であり，この中から一つ勝敗パターンを選ぶとする。あ　の勝敗パターンを決定すると い が指し分けになるパターン数は $126$ 個になり，さらにこの中から一つ勝敗パターンを選ぶ。あい の勝敗パターンを決定すると う が指し分けになるパターンは $21$ 個あるいは $35$ 個となる。平均は $31.5$ 個である。

	あ	個数
い	○	126
	×	126

	あ	い	個数
う	○	○	56
	○	×	70
	×	○	70
	×	×	56

	あ	い	う	個数
え	○	○	○	21
	○	○	×	35
	○	×	○	35
	○	×	×	35
	×	○	○	35
	×	○	×	35
	×	×	○	35
	×	×	×	21

あいうえ の勝敗パターンを決定すると お が指し分けになるパターンは $6, 15, 20$ 個となる。平均は $15.75$ 個である。

	あ	い	う	え	個数
お	○	○	○	○	6
	○	○	○	×	15
	○	○	×	○	15
	○	○	×	×	20
	○	×	○	○	15
	○	×	○	×	20
	○	×	×	○	20
	○	×	×	×	15
	×	○	○	○	15
	×	○	○	×	20
	×	○	×	○	20
	×	○	×	×	15
	×	×	○	○	20
	×	×	○	×	15
	×	×	×	○	15
	×	×	×	×	6

こうして指し分けになるパターンのみを選択するようにすれば，検索パターン数は

\begin{aligned}
126×63×31.5×15.75\times \cdots &\simeq  2^7 \times 2^6 \times 2^5 \times 2^4 \times \cdots \\
&= 2^{7+6+5+4+\cdots} \\
&= 2^{28}
\end{aligned}

となり，９人の場合と変わらないと予想される。

こうして根本からアルゴリズムを見直したプログラムを以下に示す。あ が い に勝った場合とは，逆に い は あ に負けていることになる。指し分けパターンを辿る時に勝敗を反転させるのは無駄なので最初から反転させた値を格納している。左右も反転させているのは処理効率が良いからである。

11人のリーグの場合（アルゴリズム見直し版）

// ビットマスク
int[]	mask = new int[] {
	0x03FF, 0x01FF, 0x00FF, 0x007F, 0x003F, 0x001F, 0x000F, 0x0007, 0x0003, 0x0001, 0x0000
};
// ビット反転かつ左右反転
int		bit_invert( int x, int n ) {
	int		y = 0;
	for( int i = 0; i < n; i++ ) {
		y <<= 1;
		if( ( x & 1 ) == 0 ) y |= 1;
		x >>= 1;
	}
	return( y );
}
// 「あ」の指し分けパターンを列挙する
int[]	create_list1() {
	var	list = new List<int>();
	for( int i = 0; i < 1024; i++ ) {
		int	n = 0;
		for( int j = i; j != 0; j >>= 1 ) 
			if( ( j & 1 ) != 0 ) n++;
		if( n == 5 ) 
			list.Add( bit_invert( i, 10 ) );
	}
	return list.ToArray();
}
int[]	a_list = create_list1();		//「あ」の指し分けパターン
// 「い～こ」の指し分けパターンを列挙する
int[][]	create_list2( int n ) {
	int	size = 1 << n;
	var	list = new List<int>[size];
	for( int i = 0; i < list.Length; i++ ) 
		list[i] = new List<int>();
	for( int i = 0; i < a_list.Length; i++ ) {
		int	key = a_list[i] >> ( 10 - n );
		int	val = a_list[i] & mask[n];
		list[key].Add( bit_invert( val, 10 - n ) );
	}
	var	array = new int[size][];
	for( int i = 0; i < array.Length; i++ ) 
		if( list[i].Count > 0 ) 
			array[i] = list[i].ToArray();
	return array;
}
int[][]	b_list = create_list2( 1 );		//「い」の指し分けパターン
int[][]	c_list = create_list2( 2 );		//「う」の指し分けパターン
int[][]	d_list = create_list2( 3 );		//「え」の指し分けパターン
int[][]	e_list = create_list2( 4 );		//「お」の指し分けパターン
int[][]	f_list = create_list2( 5 );		//「か」の指し分けパターン
int[][]	g_list = create_list2( 6 );		//「き」の指し分けパターン
int[][]	h_list = create_list2( 7 );		//「く」の指し分けパターン
int[][]	i_list = create_list2( 8 );		//「け」の指し分けパターン
int[][]	j_list = create_list2( 9 );		//「こ」の指し分けパターン
int	count = 0;
for( int l0 = 0; l0 < a_list.Length; l0++ ) {
	int	a = a_list[l0];
	int	k1 = a & 1;
	if( b_list[k1] == null ) continue;
	for( int l1 = 0; l1 < b_list[k1].Length; l1++ ) {
		int	b = b_list[k1][l1];
		int	k2 = ( a & 2 ) | ( b & 1 );
		if( c_list[k2] == null ) continue;
		for( int l2 = 0; l2 < c_list[k2].Length; l2++ ) {
			int	c = c_list[k2][l2];
			int	k3 = ( a & 4 ) | ( b & 2 ) | ( c & 1 );
			if( d_list[k3] == null ) continue;
			for( int l3 = 0; l3 < d_list[k3].Length; l3++ ) {
				int	d = d_list[k3][l3];
				int	k4 = ( a & 8 ) | ( b & 4 ) | ( c & 2 ) | ( d & 1 );
				if( e_list[k4] == null ) continue;
				for( int l4 = 0; l4 < e_list[k4].Length; l4++ ) {
					int	e = e_list[k4][l4];
					int	k5 = ( a & 16 ) | ( b & 8 ) | ( c & 4 ) | ( d & 2 ) | ( e & 1 );
					if( f_list[k5] == null ) continue;
					for( int l5 = 0; l5 < f_list[k5].Length; l5++ ) {
						int	f = f_list[k5][l5];
						int	k6 = ( a & 32 ) | ( b & 16 ) | ( c & 8 ) | ( d & 4 ) | ( e & 2 ) | f & 1 );
						if( g_list[k6] == null ) continue;
						for( int l6 = 0; l6 < g_list[k6].Length; l6++ ) {
							int	g = g_list[k6][l6];
							int	k7 = ( a & 64 ) | ( b & 32 ) | ( c & 16 ) | ( d & 8 ) | ( e & 4 ) | ( f & 2 ) | ( g & 1 );
							if( h_list[k7] == null ) continue;
							for( int l7 = 0; l7 < h_list[k7].Length; l7++ ) {
								int	h = h_list[k7][l7];
								int	k8 = ( a & 128 ) | ( b & 64 ) | ( c & 32 ) | ( d & 16 ) | ( e & 8 ) | ( f & 4 ) | ( g & 2 ) | ( h & 1 );
								if( i_list[k8] == null ) continue;
								for( int l8 = 0; l8 < i_list[k8].Length; l8++ ) {
									int	i = i_list[k8][l8];
									int	k9 = ( a & 256 ) | ( b & 128 ) | ( c & 64 ) | ( d & 32 ) | ( e & 16 ) | ( f & 8 ) | ( g & 4 ) | ( h & 2 ) | ( i & 1 );
									if( j_list[k9] == null ) continue;
									count += j_list[k9].Length;
								}
							}
						}
					}
				}
			}
		}
	}
	break;	// 一番外側のループを１回で終わらせる
}
Console.WriteLine( count );

結論

計算結果は次のようになった。なお，計算時間は２秒かからなかった。

\begin{aligned}
191474240 \times {}_{10}\textrm{C}_5 / 2^{55} &= 48251508480 / 36028797018963968 \\
&= 1.33925\times 10^{-6}
\end{aligned}

ということで11名全員が５勝５敗の指し分けになる確率は約75万分の１であることが分かった。

この問題の一番厄介なところは正解が分からないということであるが，グラフにしてみるとだいたい合っている感じがする。B級1組13名全員が６勝６敗の指し分けになる確率は，おそらく1000万分の１前後になると予想される。

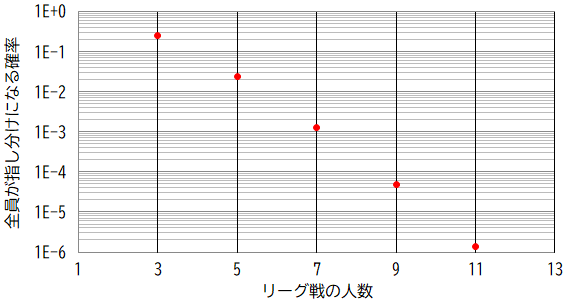
事前に検索パターン数を $2^{28} = 268,435,456$ と予想したのに対し，計算結果は $191,474,240$ となったので，まあまあ合っていたとも言える。