目的
ムーンライトワンダーチャンスの突破率を求めたい.
ムーンライトワンダーチャンスの概要
ムーンライトワンダーチャンス(以下MLWC)は以下のようなシステム.
・8球1ゲームで抽選
・当選する数字は1~25。重複はしない
・外枠の数字がヒットすればその行(or列)の風船を全て割る
・ヒットした数字はすぐに次の数字に変わる
・消滅した風船がある場合は全ての風船が上に詰め寄る
・爆弾がある風船を割れば上下左右1マスの風船も割る
・盤面の風船すべてを割ればMLWC突破
・それと別で指定の3数字全てヒットでりんご獲得(今回は無視)

画像は公式サイトより
結果
MLWCを1回の実行で1,000,000回行い成功率を求める.また、爆弾の配置は1回のWCごとにランダムとする。
本来のMLWCでは3ゲームのうち1ゲームでも突破すればMLWCが成功扱いになる.
そこで今回の結果では
A.この盤面が成功する確率
B.3ゲームこの盤面が出たとして1回以上成功する確率
をそれぞれ記載する.
サンプル検証
まずは公式サイトの矢の位置をもとに試してみる
入力数値 11,13,14,15,16
結果(突破率) A: 0.054 B: 0.153
こんな感じで求まったので今度は現状で把握している配置全てを検証してみる。結果を確率の小さかった順番に記載します。
あと比較用としてスターダストワンダーチャンスの確率(複数ナンバー型のチャンスカードなし)も記載しますね。
なおスターダストワンダーチャンスの突破率は3ゲーム通しての突破率です。
スマホで見ている場合,画像が小さい場合は配置画像をクリックするとよく見れるよ!
表の長さを節約するため、ゲーム単体での突破率を確率A、3ゲーム中1回は突破する確率を確率Bと書いています。
| WCの種類 | 矢の配置(数値) | 配置(例) |ゲーム単体での突破率
3ゲーム中1回は突破する確率|
|:-:|:-:|:-:|:-:|:-:|
|STD|6マス空き | |---
|---
8.5%|
|ML|1~10、13| |3.3%
|3.3%
9.7%|
|ML|1~10,13~15| |4.3%
|4.3%
12.3%|
|STD|5マス空き | |---
|---
13.3%|
|ML|1,2,5~12,
15,16| |5.2%
|5.2%
14.8%|
|ML|1~10,12| |5.4%
|5.4%
15.3%|
|ML|2~5,7~10
12~15| |6.9%
|6.9%
19.4%|
|STD|4マス空き | |---
|---
20.5%|
|ML|2~6,11~15| |7.5%
|7.5%
20.9%|
|ML|全埋め(1~16)| |13.9%
|13.9%
36.2%|
|STD|1マス空き | |---
|---
68.5%|
スターダストワンダーチャンスの突破率はこちらのサイト(外部ページ)を参考にしました。
結果としてはどんなに(現状把握している時点で)最悪の配置でもスターダストWCの6マス空きよりは確率があることがわかった。
考察
確率から見て12が抜けている場合はハズレ配置(スターダストワンダーチャンスでいう6マス空き)と考えていいのかなと思った。あと、「3,4,13,14空き」のMLWCの配置ではうまく行けばリーチ番号が5つになるし、確率が高い方のチャンスカードになると自分で予想はしていたが実際は下から数えたほうが早い順位だったのに驚き。
当然確率上では普通のスターダストワンダーチャンスよりは低い数値となっているがスターダストは3ゲーム全体で突破する確率、MLWCは3ゲームのうち1回以上は突破する確率のため、本来よりも低い突破率になっていると考えられる。その結果として最悪な配置では突破率3.3%しかないMLWCだが3ゲームで考えると9.7%であり、これはスターダストの6マス空きよりは高い確率となっている。
余談
このプログラム実装当時は全配置の矢は存在しないと考えていました。その理由がMLWC中にある矢とは別で存在する「指定された3つの数字にすべてヒットした場合はりんごを獲得する」というルールである。全部埋めの場合で使用する数字は16個、りんご獲得で使用する番号は3個、その状態で7こ数字を使用すると空いている数字がないんじゃないかって思ったので全配置はありえないと思っていました。しかしtwitter上では確認できたので全配置は可能ってことがわかりました。
...何が言いたいのかっていうとりんご獲得の数字と矢に記載されている番号の重複はありえるってことです。
まとめ
とりあえず最初にMLWCの矢の配置を見て、
・最悪の配置でもSTDワンダーチャンスのチャンス無し6マス空きよりは期待度が高い
・12の矢が存在しない場合は悪配置
・2~5、12~15が埋まっている配置は良配置
・3,4,13,14空きの配置は一見チャンスカードに見えてそうでも無い。
・というか12の矢があるかないかで結構変わってくる。
謝辞
MLWCの開始前サンプル画像をEさん、Jさん、Oさん、Nさん、Yさん(アルファ順)から頂きました。ありがとうございます。
関連リンク
スターダストワンダーチャンスの突破率はこちら
サンシャインワンダーチャンスの突破率はこちら
設計
ここからはプログラマー向けの章になります。また、この章以降ではPCでの閲覧を推奨します。
公式と同じような突破システムであれば多少仕様をいじったって確率上は問題ないはず。
とりあえずプログラム的に見てみよう
ゲーム盤面の数字、矢が発射される方向をアルファベットで書くとこんな感じ。
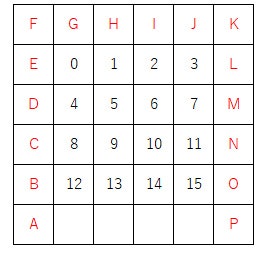
Aの数字がヒットした場合、割る風船の位置は12,9,6,3
Bの数字がヒットした場合、割る風船の位置は12,13,14,15って感じだね
んでこれをA~Pまでまとめると、
A = [ 3, 6, 9,12]
B = [12,13,14,15]
C = [ 8, 9,10,11]
D = [ 4, 5, 6, 7]
E = [ 0, 1, 2, 3]
F = [ 0, 5,10,15]
G = [ 0, 4, 8,12]
H = [ 1, 5, 9,13]
I = [ 2, 6,10,11]
J = [ 3, 7,11,15]
K = [ 3, 6, 9,12] = A
L = [12,13,14,15] = B
M = [ 8, 9,10,11] = C
N = [ 4, 5, 6, 7] = D
O = [ 0, 1, 2, 3] = E
P = [ 0, 5,10,15] = F
とまあM~Pに関してはA~Fと全く同じ。発射方向が真逆なだけで同じ線上にあるからね。
とりあえず作りやすくする
配列は横のほうがわかりやすい(よね?)なので風船が動く方向...っていうか全部-90度回転させる

これによって
・矢の発射位置が変化する。←方向の矢はなくなる
・風船の移動方向が左方向になる
・二次元配列で列ごとに移動させなくてすむ。
・行で移動するため処理がめちゃくちゃしやすい!
それによってさっきのA~Pの位置はこうなるね、

で、アルファベットの対象数字も変わるので
A = K = [ 0, 5,10,15]
B = L = [ 0, 4, 8,12]
C = M = [ 1, 5, 9,13]
D = N = [ 2, 6,10,11]
E = O = [ 3, 7,11,15]
F = P = [ 3, 6, 9,12]
G = [12,13,14,15]
H = [ 8, 9,10,11]
I = [ 4, 5, 6, 7]
J = [ 0, 1, 2, 3]
K = [ 0, 5,10,15]
今後の実装ではこれをベースに考えて行きます。
数字のヒット方式を変える
従来手法
公式のMLWCではヒットした数字が埋まっていない数字に変わる。
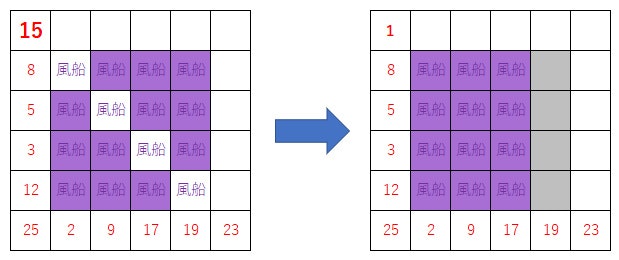
例えば上記図では15がヒットし斜め1列(?)を消した。ヒットした15はまだ埋まっていない数字に切り替わる(今回は1)
今回の設計改善案
これを→ヒットした数字を消し、全部時計回りに移動させる。

15がヒットしたあと、全ての数字が時計回りに詰めて今回なら8が左上に移動し、それ以外の数字は順番に時計回りに詰める。新しい数字は11。
なぜこれが楽になるか
リストで埋まった数字のつけ変えが省ける。
仮に数字リストが1~9だけ、当選枠はA~Dのみで処理を考えてみる。
従来手法の場合:
1.当選数字を外す
2.新しく当選数字を保留リストから抽選する
当選数字が保留リストなら外す必要がある
3.新しい当選数字を当選枠に埋める
4.保留枠の数字をつめる
この処理を新しい提案手法では数字リストを[当選リストと保留リスト]をくっつけた一つのリストとして
1.当選数字を外す
保留リストの数字が当選してもそのまま外す
2.数字を右に詰める
以上!!かんたん!!
と、アルゴリズム的(?)には処理が大きく縮まるので助かる。

実装
ここ以前の章では個人的なわかりやすさのたと入力のしやすさのため,矢の配置はアルファベットではなく数字の1~16で記載する.
さて、プログラムを作成するための工夫を充分に説明したので作成の実装に取り掛かる。プログラムの流れを考えると
1.発射する矢の位置を決定する
2.指定の部分すべて取り除くまで1を繰り返し行う
3.MLWCを指定回数分行う(単純に求めるなら10万、統計で出すなら100万回ほど)
4.結果を出力
それぞれを細分化して実装する。
0.下準備
実行時に毎回変わるようにするのは大事.
んで,出力は見やすいほうが良いので色文字で.
class pycolor:
BLACK = '\033[30m'
RED = '\033[31m'
GREEN = '\033[32m'
YELLOW = '\033[33m'
BLUE = '\033[34m'
PURPLE = '\033[35m'
CYAN = '\033[36m'
WHITE = '\033[37m'
END = '\033[0m'
色文字の出力方法に関してはこちらの方の記事をご覧ぐださい.
そしてゲーム盤面を見やすく表示するための関数を作成する.
def printrow(a):
for i in range(len(a)):
for k in range(len(a[i])):
if a[i][k] == 0:print(pycolor.BLACK + "□" + pycolor.END,end = '')
if a[i][k] == 1:print(pycolor.YELLOW + "●" + pycolor.END,end='')
if a[i][k] == 2:print(pycolor.RED + "◎" + pycolor.END,end='')
if a[i][k] == 3:print(pycolor.GREEN + "◆" + pycolor.END,end='')
print()
print()
def printboard(a):
for i in range(len(a)):
for k in range(len(a[i])):
if a[i][k] == "●":print(pycolor.YELLOW + "●" +pycolor.END,end='')
elif a[i][k] == "--":print(pycolor.BLUE + "--" + pycolor.END,end='')
else: print(pycolor.GREEN + a[i][k] + pycolor.END,end='')
print()
print()
(1. 2.)発射する矢の位置を決定する
単純入力で0が入力されるまで外す矢の番号を入力してもらう.
preboard = [
[" 6"," 7"," 8"," 9","10","11"],
[" 5","●","●","●","●","12"],
[" 4","●","●","●","●","13"],
[" 3","●","●","●","●","14"],
[" 2","●","●","●","●","15"],
[" 1"," "," "," "," ","16"],
]
printboard(preboard)
while x:
x = int(input())
if x == 0:break
print("removed",x)
linethrower[x-1] = 0
rem = preboardplace[x-1]
preboard[rem[0]][rem[1]] = "--"
printboard(preboard)
print("Remove complete. start MLWC.")
0を入力でMLWC開始.ここからMLWCの処理を開始する.
3.MLWC部分の実装
3.1 MLWCの下準備
まずはゲーム盤面の準備.変数名boardで4x4の盤面を用意
風船は1
爆弾あり風船は2
マスに矢が通った場合,爆弾により割れた場合は3
空マスは0
としてあつかう.
そして次に1ゲームで選ばれる8つの数字とヒット対象のなる数字の並べ替えの変数を用意
board = copy.copy([[1 for i in range(4)] for k in range(4)])
board[rand(4)][rand(4)] = 2
choose = r.sample(range(25), k=8)
deck = r.sample(range(25), k=25)
なんでboard作成でcopy関数を?っていうのは保険で使ってます.
3.2 8球の抽選処理を行う
8球の抽選の流れで
A.指定された数字が配列で0~15番目以内に存在するか
B.Aが真の場合,矢を投げる対象の数値であるか
を1球ごとに判定をする.
もしA,B共に真である場合は矢を投げる.
3.3 爆弾の処理
もし矢を投げてboard内の2っていう数字がヒットした場合は変更を行う
board内の上下左右の位置を消せばいいが...爆弾が端っこにあると-1マス目や4マス目を参照してしまうのでエラーを吐かれてしまう.
そこでそれぞれの方角で爆弾の位置が0~15で:
・4以上なら上の爆弾を消す
・11以下なら下の爆弾を消す
・4で割ったあまりが3以外なら右の爆弾を消す
・4で割ったあまりが0以外なら左の爆弾を消す
って言う処理を行えば解決!
3.2と3.3の処理をまとめるとこんな感じに
for a in choose:
count+=1
#print(count,"球目")
pos = deck.index(a)
if pos < 16: #矢が本来ある位置,の対象枠である場合.
if linethrower[pos]: #今回のMLWCで矢が存在する場合
for i in line[pos]:
x = i%4
y = i//4
#ここの処理は爆弾ありで考える
if board[i//4][i%4] == 2:
if i > 3: board[y-1][x] = 3 #上の風船を割る
if i < 11:board[y+1][x] = 3 #下の風船を割る
if i%4 != 3:board[y][x+1] = 3 #右の風船を割る
if i%4:board[y][x-1] = 3 #左の風船を割る
board[i//4][i%4] = 3
for i in range(4):
p = 0
while p<4:
while board[i][p] == 3:
board[i].pop(p)
board[i].append(0)
p+=1
deck.pop(pos) #当選した番号は矢の有無にかからわず消す
3.4 MLWCの成功判定
board全てのマスが0なら成功→各行のsumを足して0になれば成功扱いになる.
s = 0
for i in range(4):
s+=sum(board[i])
if s == 0: cleared+=1
以下ソースコード
今後の検証用としてもおいておきます(今回の結果でもしも間違っているものがればコメントをお願いしたいです.)
import random as r
import copy
def rand(x):
return r.randrange(x)
def printrow(a):
for i in range(len(a)):
for k in range(len(a[i])):
if a[i][k] == 0:print(pycolor.BLACK + "□" + pycolor.END,end = '')
if a[i][k] == 1:print(pycolor.YELLOW + "●" + pycolor.END,end='')
if a[i][k] == 2:print(pycolor.RED + "◎" + pycolor.END,end='')
if a[i][k] == 3:print(pycolor.GREEN + "◆" + pycolor.END,end='')
print()
print()
def printboard(a):
for i in range(len(a)):
for k in range(len(a[i])):
if a[i][k] == "●":print(pycolor.YELLOW + "●" +pycolor.END,end='')
elif a[i][k] == "--":print(pycolor.BLUE + "--" + pycolor.END,end='')
else:print(pycolor.GREEN + a[i][k] + pycolor.END,end='')
print()
print()
class pycolor:
BLACK = '\033[30m'
RED = '\033[31m'
GREEN = '\033[32m'
YELLOW = '\033[33m'
BLUE = '\033[34m'
PURPLE = '\033[35m'
CYAN = '\033[36m'
WHITE = '\033[37m'
END = '\033[0m'
BOLD = '\038[1m'
UNDERLINE = '\033[4m'
INVISIBLE = '\033[08m'
REVERCE = '\033[07m'
line =[[0,5,10,15],[3,7,11,15],[2,6,10,14],[1,5,9,13],[0,4,8,12],[3,6,9,12],[12,13,14,15],[8,9,10,11],[4,5,6,7],[0,1,2,3],[0,5,10,15],[0,4,8,12],[1,5,9,13],[2,6,10,14],[3,7,11,15],[3,6,9,12]]
preboardplace =[ [5,0],[4,0],[3,0],[2,0],[1,0],[0,0],[0,1],[0,2],[0,3],[0,4],[0,5],[1,5],[2,5],[3,5],[4,5],[5,5] ]
linethrower = [i+1 for i in range(16)]
print("外す番号を入力して下さい")
x = 1
preboard = [
[" 6"," 7"," 8"," 9","10","11"],
[" 5","●","●","●","●","12"],
[" 4","●","●","●","●","13"],
[" 3","●","●","●","●","14"],
[" 2","●","●","●","●","15"],
[" 1"," "," "," "," ","16"],
]
printboard(preboard)
while x:
x = int(input())
if x == 0:break
print("removed",x)
linethrower[x-1] = 0
rem = preboardplace[x-1]
preboard[rem[0]][rem[1]] = "--"
printboard(preboard)
print("Remove complete. start MLWC.")
cleared = 0
attempts = 100000
for loop in range(attempts):
if (loop+1)%5000==0:print("\r",loop+1,end ="")
board = copy.copy([[1 for i in range(4)] for k in range(4)])
board[rand(4)][rand(4)] = 2
choose = r.sample(range(25), k=8)
deck = r.sample(range(25), k=25)
linedeck = []
#printrow(board)
count = 0
for a in choose:
count+=1
#print(count,"球目")
pos = deck.index(a)
if pos < 16: #矢が本来ある位置,の対象枠である場合.
if linethrower[pos]: #今回のMLWCで矢が存在する場合
for i in line[pos]:
x = i%4
y = i//4
#ここの処理は爆弾ありで考える
if board[i//4][i%4] == 2:
if i > 3: board[y-1][x] = 3 #上の風船を割る
if i < 11:board[y+1][x] = 3 #下の風船を割る
if i%4 != 3:board[y][x+1] = 3 #右の風船を割る
if i%4:board[y][x-1] = 3 #左の風船を割る
board[i//4][i%4] = 3
for i in range(4):
p = 0
while p<4:
while board[i][p] == 3:
board[i].pop(p)
board[i].append(0)
p+=1
deck.pop(pos) #当選した番号は矢の有無にかからわず消す
#printrow(board)
#print(choose)
#print(deck)
s = 0
for i in range(4):
s+=sum(board[i])
if s == 0: cleared+=1
print()
print(cleared)
print(pycolor.CYAN + "1ゲーム内で突破する確率" + pycolor.END,round(cleared/attempts,3))
rate = cleared/attempts
print(pycolor.CYAN + "3ゲームこの盤面が出てうち1回は突破する確率" + pycolor.END,round(1-pow(1-rate,3),3))
