本システムの内容
本来はゲーム内でワンダーチャンスというシステムで有り、一定条件を満たすとジャックポットチャンスに突入するが、ここでは内容の部分では成功、失敗などと説明する。
・全16マスあるすごろくゲーム
・1~8マス進行する。
・1ゲーム8球、1~25のうち8球入賞(1ゲーム間では重複なし)
・1~25で入賞した数字/3の数進む(ただし25のみ例外で8マス進む)
・止まったマスのキャラ分(アニマ)合計回収数に加算される。
・2ゲーム目、3ゲーム目の開始時に一部マスアニマが追加される。
・通して3ゲーム行い合計で集めたアニマ数が20体以上で成功になる。
・例外で合計9体以下の場合は裏ボーナスA、12体以下の場合はボーナスBを獲得する。
なおここではそれぞれの名称を以下のように章によって記載する。
スターダストワンダーチャンス→STDWC
ムーンライトワンダーチャンス→MLWC
サンシャインワンダーチャンス→SSWC
ゲームシステムの把握
設定差
開始時の振り分け
現状このすごろくで把握しているのはアニマが2体あるマスとアニマが1体あるマスがあり、ゲーム開始時に合計アニマが18体になるように組み合わせられる。把握しているのは現状で6パターン。
| アニマx2マス | アニマx1マス | 空きマス |
|---|---|---|
| 4 | 10 | 2 |
| 5 | 8 | 3 |
| 6 | 6 | 4 |
| 7 | 4 | 5 |
| 8 | 2 | 6 |
| 9 | 0 | 7 |
ゲーム間のアニマ追加
ゲーム間に一部空きマスにアニマx1が補充される。追加されるマス数は2~4であるが3はたまに見る程度であり、4マス追加は滅多に見れない。ここでは追加確率の振り分けを以下のように分ける。
| 条件 | 確率 |
|---|---|
| 2マス追加 | 85% |
| 3マス追加 | 10% |
| 4マス追加 | 5% |
ただし上記条件で十分な空きマス数が満たせない場合は可能な限り最大まで増やす。
実行結果
それぞれの突破率を記載する。また、参考として他の種類の突破率も記載する。ムーンライトWC、サンシャインWCの突破率に関しては100万回行ったWCの中で成功した回数を数え、それを%として表記している。
サンシャインWCでは配置するアニマx1、アニマx2マス数は決まっていますが、毎回ランダムに配置しています。
|種類 | 内容 | 確率 | 配置例|
|:-:|:-:|:-:|:-:|:-:|
STD | nマス空き(1枠に複数ナンバー無し) | --- | ←見本1
ML | 複数カードを平均した数値 | --- | ←見本2
SS | anima x2マス数(anima x1マス数) | --- | ←見本3|
|----|----|----|----|----|
SS | 4マス(10マス) | 8.0% | 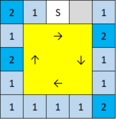
STD | 6マス空き | 8.5% | 
SS | 5マス(8マス) | 9.1% |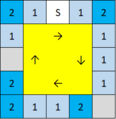
ML | 最低ライン | *9.7% | |
SS | 6マス(6マス) | 10.4% |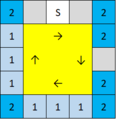
SS | 7マス(4マス) | 11.5% |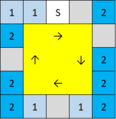
SS | 8マス(2マス) | 12.5% |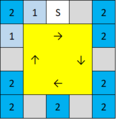
ML | 通常カード平均ライン | *13.0% |
STD | 5マス空き | 13.3% | 
SS | 9マス(無し) | 13.3% | 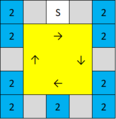
ML | 全カード平均ライン | *18.6% |
STD | 4マス空き | 20.5% |  |
|
ML | チャンスカードのみ平均ライン | *25.7% | |
STD | 1マス空き | 68.5% |  |
|
*ムーンライトワンダーチャンス(MLWC)で記載されている突破率は3ゲーム中に1回は突破する確率となっています。1ゲーム内での突破率ではありません。
スターダストワンダーチャンスの突破率はこちらのサイト(外部ページ)を参考にしました。
考察やその他もろもろ
ここからの考察は大部分がメダルゲーマー向けとなっています。ご了承ください。
いや低くね!?
最低カードでの突破率が8.0%、一番状態がいいチャンスカードでも13.3%ってどうなの?流石に低すぎて今でも自分のソースコードを疑ってる。
もし間違っている場所があったら誰か教えて下さい…
実際との比較
今回の記事を作成するにあたり、複数人のレコード情報よりサンシャインWCを遊んだ回数とサンシャインジャックポットチャンスに突入した回数、つまりSSWCの成功回数(一部例外あり)や成功確率をまとめて集計した。その統計をまとめたところ、試行回数482回で成功回数が58回であったため、確率は12.0%であった。
今回の集計結果と実際のWC統計では少しWCの統計が上振れになっていると考えられる。このようになったと考えられる理由としてはカードの上振れ、ソースコードの間違い、母数不足が考えられる。
クソゲーと評価される理由について
今回の結果はSTDWCのチャンスなし6マスより平均的な数値は高い。しかしSSWCはクソゲーと評価される。実際にアンケートを取ってみた結果、投票数こそ少ないものの約半数がクソゲーと評価するようになった。
STDWCではJPCに行かなかったとき、一定の基準を満たすと配当を獲得できる上にワンダーステップを獲得できる。しかしSSWCの方ではMLWCの方と同じように失敗した場合は配当のみの獲得であり、ワンダーステップを獲得することはできない。そのためSTDWCでは成功、失敗、妥協ができる失敗の3種類、SSWCでは成功か失敗かの2つのみで見ているため、クソゲーとして評価されるのでは無いかと考えられる。
Q&A
一部のユーザーから頂いた質問、疑問についてここで解説をしていく
Q.りんご3つや裏ボーナスの獲得率は?
A.りんご3つはほぼ1%以下。一方裏ボーナス極稀
各アニマx2マスとりんご3つ獲得率や裏ボーナス率を見ると以下の様になる。
| アニマx2のマス数 | りんご3つ率(回収10~12) | 裏ボーナス(回収9以下) |
|---|---|---|
| 4 | 0.5% | 0.001% |
| 5 | 0.7% | 0.004% |
| 6 | 0.9% | 0.008% |
| 7 | 1.3% | 0.01% |
| 8 | 1.5% | 0.02% |
| 9 | 1.9% | 0.06% |
りんご3つは最上位カードを引けば誤差レベルで取りやすくなる。9体以下の回収は極稀であるため、あまり気にしなくて良いと考えられる。
Q.空きマスやアニママスが偏っているほうが有利とかある?
A.バラけている方が有利だが誤差。気にすんな。
検証方法としてアニマ9体を最初の9マスに寄せる。(下記画像参照)
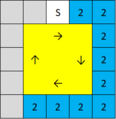
突破率を比較するとこんな感じ。
| 種類 | 突破率 |
|---|---|
| バラバラ(ランダム) | 13.3% (上記表の通り) |
| 偏り | 13.5% (今回の検証) |
結果バラけたものよりも偏っている方が有利ではあったがその差は0.2%であり、WC1000やったうちの2回ほどの差しか無いため誤差であると考えで良いと思う。
Q.0体獲得って可能?
A.可能。でもほぼ無理。
例えば下記画像のパターンとかなら0体回収も可能である。
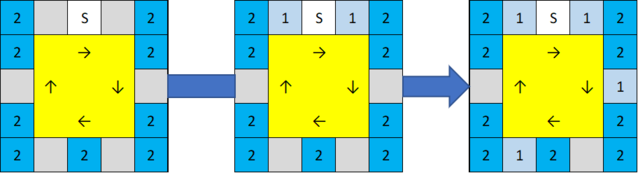
しかし0体回収を達成するにはアニマx2マスが9マスであることと最終ゲームでハズレマスが等間隔ではいことが必須である。
(つまり達成できたらすごいよ!)
まとめ
まとめるとサンシャインワンダーチャンスは:
・突破率は8%~13%で計算式の目安は6%+(開始マス含む空きマス数)%
・チャンスカードであったとしてもMLWCやSTDWCのように突破率が高いわけではない
・アニマx2のマスが多いほうが有利
・裏ボーナスもアニマx2のマスが多いほうが有利
謝辞
今回のプログラムを作成するにあたって有益な情報を提供していただいたたろたるさん、ありがとうございました。
また、サンシャインワンダーチャンスの配置例やレコードを画像を提供していただいた多数の方々、ありがとうございました。
関連リンク
スターダストワンダーチャンスの突破率はこちら
ムーンライトワンダーチャンスの突破率はこちら
プログラムの設計
ここからはプログラマ向けの説明を順番に行う。ここではアニマx2のマス数が7、アニマx1のマス数が4の空きマスが5マスのワンダーチャンス盤面を作成する。
盤面の作成
すごろく長さは16であるため、変数boardに長さ16の配列、2と1を組み合わせた合計18になるような配列を作成する。作成の手順として
1.配列に1を4回追加する。
2.配列に2を7回追加する。
3.配列に0を5回追加する。
という手順で行う。ここで4,7,5の決定方法だがアニマx2のマス数をあらかじめ決定することでその他の数字が自動的に決まるようになる。
上記手順が完了したあとワンダーチャンスの盤面を毎回ランダムにするため、配列をシャッフルする。シャッフルが完了したら最後に0番目に0を追加し、サンシャインWCの盤面が完成する。
board = []
double = 9
single = 18 - 2*double
open = 15-single -double
collected = 0
for i in range(single): board.append(1)
for i in range(double):board.append(2)
for i in range(open):board.append(0)
r.shuffle(board)
board.insert(0,0)
抽選番号の決定
本来のアニマロッタでは1~25で抽選し、入った番号によって1~8マス進む。ここでは簡略化するためにまず1~8をそれぞれ3回ずつ追加し、最後に8を1個追加する。これで配列は1112223334445556667778888になる。最後にこれをシャッフルして先頭から8つ分進む処理を行う。
deck = []
for i in range(1,9):
for k in range(3):
deck.append(i)
deck.append(8)
r.shuffle(deck)
ゲーム盤面で進む処理
ゲーム中の処理
配列の先頭から順番に見ていきdeck内にある数字分pos(現在いるマス)を進める。ただしposが16を超えた場合は16で割ったあまりを取得する。もし到着したマスにアニマがいる場合はその数の回収を行う。この処理は8回しか行わない
ゲーム間の処理(アニマ追加)
100の中から乱数を選択し、出た数字によって追加するアニマ数を決定する。もし引いた乱数が6以下かつ空きマスが4つ以上あるなら3つアニマ追加を、引いた乱数が2以下かつ空きマスが5つ以上あるなら4つアニマを追加する。
for game in range(1,4):
for i in range(8):
pos+=deck[i]
pos%=16
collected+=board[pos]
board[pos] = 0
if game < 3:
roll = rand(100)
add = 2
open_spaces = board.count(0)
if roll < 15 and open_spaces >= 4: add+=1
if roll < 5 and open_spaces >= 5:add+=1
for i in range(add):
p = rand(16)
while board[p] or p == pos: p = rand(16)
board[p] = 1
結果出力
3ゲーム目終了時、獲得した数によって報酬が異なる。まず1回の集計を行うごとに獲得したアニマ数を変数finalizeにカウンターとして1追加する。そして9以下、12以下、15以下、17以下、18、19、20以上で最終的には出力を分けるようにする。
print(sum(finalze[0:10]))
print(sum(finalze[10:13]))
print(sum(finalze[13:16]))
print(sum(finalze[16:18]))
print(finalze[18])
print(finalze[19])
print(sum(finalze[20:]))
以下全体のソースコード
import random as r
import copy
def rand(n):
return r.randrange(n)
finalze = [0 for i in range(30)]
for loop in range(1000000):
if (loop+1)%5000==0:print("\r",loop+1,end ="")
board = []
double = 4
single = 18 - 2*double
open = 15-single -double
collected = 0
for i in range(single): board.append(1)
for i in range(double):board.append(2)
for i in range(open):board.append(0)
r.shuffle(board)
board.insert(0,0)
pos =0
deck = []
for i in range(1,9):
for k in range(3):
deck.append(i)
deck.append(8)
r.shuffle(deck)
for game in range(1,4):
for i in range(8):
pos+=deck[i]
pos%=16
collected+=board[pos]
board[pos] = 0
if game < 3:
deck = copy.copy([])
for i in range(1, 9):
for k in range(3):
deck.append(i)
deck.append(8)
r.shuffle(deck)
roll = rand(100)
add = 2
open_spaces = board.count(0)
if roll < 15 and open_spaces >= 4: add+=1
if roll < 5 and open_spaces >= 5:add+=1
for i in range(add):
p = rand(16)
while board[p] or p == pos: p = rand(16)
board[p] = 1
finalze[collected]+=1
print()
print(double,single,open)
print(sum(finalze[0:10]))
print(sum(finalze[10:13]))
print(sum(finalze[13:16]))
print(sum(finalze[16:18]))
print(finalze[18])
print(finalze[19])
print(sum(finalze[20:]))