Nelder-Mead Method(シンプレックス法)でパラメータチューニングに挑戦

#はじめに

深層学習等のパラメータチューニングの自動調整にはOptuna等のフレームワークが使用される。自作したらどうなるか、と言う興味が沸いたので実際にやってみた。割と原始的なNelder-Mead Methodで実装し、Cifra10の認識精度でOptunaと比較する。

Nelder-Mead Methodとは

「シンプレックス法」や「アメーバ法」と言う名前でも知られる、最適化問題のアルゴリズム。
Wikipediaの記事によると1965年に発表されたようで、かなり昔から存在する。
こちらの記事の図解がわかりやすい。実際に探索の様子を動画にしたものも複数あるようだ。
幾何学的なイメージがしやすく、いかにもアルゴリズムと言う感じがして面白い。

パラメータチューニングも最適化問題なので、応用可能である。
記事内では単純なので「シンプレックス法」の名称を使う。

実装

Optuna風に使えるように実装してみたのがこちら。
コード中の変数名はWikipediaの擬似コードに寄せた。

import numpy as np

import collections
import datetime
from pytz import timezone
import math
import sys
class Struct:
    def __init__(self, **entries):
        self.__dict__.update(entries)
class Simplex:
    def __init__(self, lmbd=0.5, adaptive=False):
        self.lmbd = lmbd
        self.adaptive = adaptive
        self.params = collections.OrderedDict()
        self.trials = []
        self.best_value = sys.float_info.max
        self.best_step = 0

    def optimize(self, objective, n_trials):
        self.info( f'Start : n_trials={n_trials} lmbd={self.lmbd} adaptive={self.adaptive}' )
        self.step= 0
        
        def next():
            value = objective(self)
            params = {}
            for index, key in enumerate(self.params):
                param = self.params[key] 
                vals = param['val']
                params[key] = vals[self.step] if not param['log'] else math.pow(10, vals[self.step])
            
            self.trials.append(Struct(value=value,params=params))
            self.step += 1

            if value < self.best_value:
                self.best_step = self.step
                self.best_value = value
                self.best_params = params
            self.info(f'Step[{self.step}] Value:{value}, Params:{params}, Best step is {self.best_step}')
            return value
        def append_next_point(point):
            for index, key in enumerate(self.params):
                param = self.params[key] 
                vals = param['val']
                vals.append( max(min(point[index], param['high']), param['low']) )
        
        ndim = -1
        while self.step < n_trials:
            if self.step == 0:
                next()
                ndim = len(self.params)
                self.alpha = 1.0
                if self.adaptive and ndim>=2:
                    self.gamma = 1 + (2.0/ndim)
                    self.rho = 0.75 - 1.0/(2*ndim)
                else:
                    self.gamma = 2.0
                    self.rho = 0.5
                for index, key in enumerate(self.params):
                    param = self.params[key] 
                    vals = param['val']*(ndim+1)
                    high = param['high']
                    low = param['low']
                    center = (high+low)/2
                    vals[int(index+1)] = center + self.lmbd*(high-center)
                    param['val'] = vals
                self.indices = np.arange(ndim+1)
            elif self.step <= ndim:
                next()
            elif self.step > ndim:
                if self.step==4:
                    print('g')
                points = np.zeros((ndim, ndim+1))
                for index, key in enumerate(self.params):
                    param = self.params[key] 
                    vals = param['val']
                    points[index] = np.take(vals, self.indices)
                points = points.transpose()
                values = np.array([ self.trials[i].value for i in self.indices ])
                sorted_indices = np.argsort(values)
                self.indices = self.indices[sorted_indices]

                sorted_values = values[sorted_indices]
                sorted_points = points[sorted_indices]
                # calc centroid
                x_0 = np.mean(sorted_points[:-1], axis=0)

                # calc reflection point
                x_n_1 = sorted_points[-1]
                x_r = x_0 + self.alpha * (x_0 - x_n_1)
                f_x_n_1 = sorted_values[-1]
                f_x_n = sorted_values[-2]
                f_x_1 = sorted_values[0]
                append_next_point(x_r)
                f_x_r = next()
                if n_trials==self.step:
                    break

                if f_x_1 <= f_x_r < f_x_n:
                    # Reflection
                    self.indices[-1] = self.step-1
                elif f_x_r < f_x_1:
                    #Expansion
                    x_e = x_0 + self.gamma*(x_r - x_0)
                    append_next_point(x_e)
                    f_x_e = next()
                    if f_x_e < f_x_r:
                        self.indices[-1] = self.step-1
                    else:
                        self.indices[-1] = self.step-2
                else:
                    # Contraction
                    x_c = x_0 + self.rho*(x_n_1 - x_0) 
                    append_next_point(x_c)
                    f_x_c = next()
                    if f_x_c < f_x_n_1:
                        self.indices[-1] = self.step-1
                    else:
                        # Shrink (not implemented)
                        self.indices[-1] = self.step-2
        self.info( f'End : Best Value: {self.best_value} , Params: {self.best_params}')

    def info(self,message):
        current_time = datetime.datetime.now().strftime('%Y-%m-%d %H:%M:%S.%f')
        print(f'\x1b[0;32m[{current_time}]\x1b[0m' +message)

    def suggest_float(self, name, low, high, log=False):
        if self.step==0:
            if low>=high:
                raise ValueError("The high value should be greater than the low value.")
            if log:
                high = math.log10(high)
                low = math.log10(low)
                val = (high+low)/2
                self.params[name] = { 'low':low, 'high':high, 'val':[val], 'log':log }
                val = math.pow(10, val)
            else:
                val = (high+low)/2
                self.params[name] = { 'low':low, 'high':high, 'val':[val], 'log':log }
            return val
        else:
            val = self.params[name]['val'][self.step]
            if log:
                return math.pow(10,val)
            return val

最低限の機能しかないが、単純課題ならばこれだけでなんとかなってしまう。

Optunaはこんな感じで使う(Tutorialから引用)。

def objective(trial):                        # 目的関数の定義
    x = trial.suggest_float("x", -100, 100)  # 区間　[-100, 100]　から適当な x を決める
    return (x - 2) ** 2                      # 目的関数の計算結果を返す
study = optuna.create_study()
study.optimize(objective, n_trials=100)

一方今回作成したSimplexクラスではこんな感じ。

def objective(trial):                        
    x = trial.suggest_float("x", -100, 100)  
    return (x - 2) ** 2                     
study = Simplex()
study.optimize(objective, n_trials=100)

真似したので当然だが、ほぼ同じように使える。
上記実行するとOptunaでは1.7113882491063444、Simplexでは1.9999999999999574となった。Simplexはランダム要素はないので、この場合は毎回同じ結果になる。

アルゴリズムの性質上、"変数の数＋１"の試行が必ず必要で、その地点は決め打ちになる。
今回の実装では、開始点は各変数の探索区間の中心として、そこから各変数をそれぞれ一定の割合でずらして試行することで、"変数の数+1"の試行になる。ずらす割合はlmbdとして指定できる(デフォルトは0.5)。上の例では開始点が0で二番めが100*0.5=50となる。
最近Adaptive Nelder-Mead Simplexと言うのが提案されていて、その内容を反映させる場合はadaptive=Trueとする。（実験では使用しない）

コード内でもコメントしてあるが、本来は縮小(Shrink)の操作があるのだが、パラメータチューニングでこれをやると試行回数が増えてしまうので、実装していない。

#実験

CIFAR10の認識精度(エラー率)でOptunaと比較する。
CNNモデルとしてはDavidNetと呼ばれるやや特殊なResNetを使う。これは「いかに短時間でCIFAR10認識値率94%を越えられるか」と言うことを目的に作られたモデルで、こちらの記事も参照のこと。ColabのTPUでは１試行に約１分程度で比較的テストしやすい。

モデルにはscalingという謎のパラメータがあるが、これは最後のActivationの直前に掛ける係数で、ここで調整しないとうまく精度がでない。今回はこのパラメータも最適化の対象とする。
学習率、Weight Decay、scaling、Warmup期間(全体に対する比率)の4つを対象として、元々のモデル推奨値付近で探索させる。

項目	スケール	Min	Max	推奨値
Learning Rate	Log	0.01	10	0.4
Weight Decay	Log	0.00001	0.01	0.0005
Scaling	Linear	0.05	1.0	0.125
Warmup	Linear	0.02	0.5	0.21(5/24)

一回の試行で24エポック学習させ、最後にValidation Setで評価する。
先に述べたように、94%を目指す設計なので、エラー率6.0前後になることが期待される。
元々はカットアウトありでの学習をさせるが、ばらつきが増えそうなので今回は使用しない。

google colab ノートブック

##実験結果

試行数は50として、Optunaは２回実施。
先に記した通り、Simplexは最初試行が決め打ちになるので、lmbdを0.5,-0.5,0.75と変えて実施。符合を変えると最初の探索方向が逆になる。数値を大きくすると探索範囲が広くなることが予想される。
環境はGoogle Colab TPU。

以下実験結果(エラー率なので小さい方が好成績)。

手法	最高値	学習率	Weight Decay	Scaling	Warmup
Optuna(1st)	6.10	0.46	0.00012	0.114	0.203
Optuna(2nd)	6.29	1.02	0.00021	0.219	0.489
Simplex(0.5)	5.98	0.26	0.00049	0.191	0.316
Simplex(-0.5)	5.82	0.35	0.00049	0.146	0.295
Simplex(0.75)	6.05	0.27	0.00069	0.347	0.410
推奨値	NA	0.4	0.0005	0.125	0.21

自分で作っておいてなんだが、なぜかSimplexの方が成績が良かった。Simplex(-0.5)では比較的推奨値に近いパラメータが得られた。
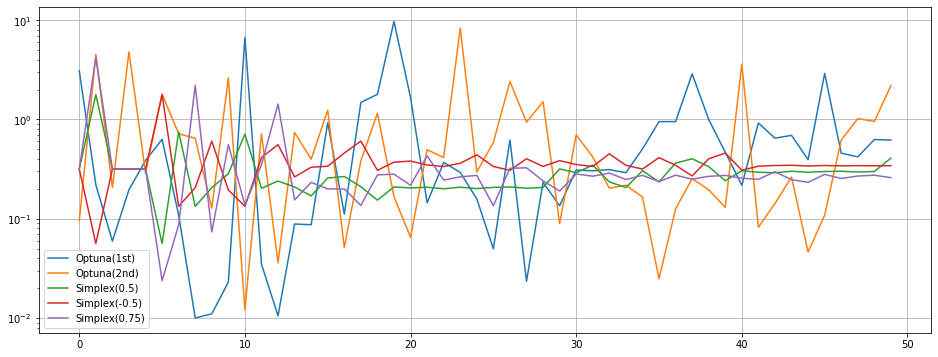
学習率の遷移をグラフにすると以下のようになった。

以下所見。

• Optunaの方が探索のばらつきが多く、より広範囲を探索しているように見える。
• Optunaの1stと2ndで最適値となったパラメータが結構違う。
• 学習率の推移を見ると、Simplexは後半は全て同じような値に収束している。逆に言えば、局所最適解に陥る可能性が高そう。
• Simplexは収束が早くばらつきが少ないので、収束値付近での試行が増えて最高値がでやすくなる確率が高かったかもしれない。

試行中の最高値の比較だけでは単に運が良かった可能性を否定できないので、それぞれ最高値を出したパラメータで１０回実施して比較してみたのがこちら。

手法	Min	Average	Max
Optuna(1st)	6.22	6.38	6.51
Optuna(2nd)	6.23	6.46	6.76
Simplex(0.5)	5.89	6.24	6.47
Simplex(-0.5)	5.93	6.16	6.35
Simplex(0.75)	6.01	6.41	6.79
推奨値	5.95	6.12	6.30

やはりSimplexの結果の方が良かった。
推奨値は経験的に得られた値のはずだが、結局推奨値が一番良いようだ。

#まとめ

シンプレックス法でパラメータチューニングができることを示した。
Optunaより実験結果が良かったのは少し受け入れ難いが、今回は探索対象や範囲がSimplexに有利な条件だったと言う風に解釈しておく。