測定データの解析②-ヒストグラムとフィッティング,lmfitのすゝめ-

まえがき

某日ミーティング、
教「T君、このグラフのフィットもうちょっとうまくできない？」
　「フィットする範囲を変えたり重み付けをすることってできない？」
T 「・・・やってみます」

といった具合でフィッティングに手を加えたいとのこと。気まぐれに解析手順の変更を求められることが多く、それに対応するのは中々に大変。その場でパパっとできるようになりたいです。

今回はscipy.optimize.curve_fitではなく、新しくlmfitというライブラリを取り入れてみます。
scipyを使ったフィッティングは測定データの解析①-scipyフィッティングの覚書-にて行いました。
コーディングはJupyter上で行っております＆Jupyter推奨です。

lmfitをうまく紹介できればいいなと思います。

GithHubにもnotebookとサンプルデータがあります。こちらから

lmfit について

lmfitはscipy.optimizeの上位互換として開発されています。
フィッティングする際にパラメータを拘束したり、誤差に重みづけをすることができます。
オブジェクトに色々な情報を追加していきながら最後にfitコマンドを実行して最適化…といった感じで動くようです。使い慣れるとscipyよりも便利かと思います。

今回の実験

測定器からはパルスデータが得られました。まず、パルスの波高値でヒストグラムを作ります。その後、フィッティングを行い、スペクトルの鋭さを評価します。
加えて、lmfitの重みづけオプションを使うことで鋭さの改善を試みます。

データの読み込み

測定器から掃きだされたパルスデータをpandasで読み込みます。今回もtkinterを使ってファイルパスを繋ぎます。

.ipynb

import tkinter 
from tkinter import filedialog
import numpy as np
import pandas as pd

root = tkinter.Tk()
root.withdraw()
file = filedialog.askopenfilename(
title='file path_',
filetypes=[("csv","csv")])
if file:
    pulse = pd.read_csv(file,engine='python',header=0,index_col=0)

pulse.iloc[:,[0,1,2]].plot()

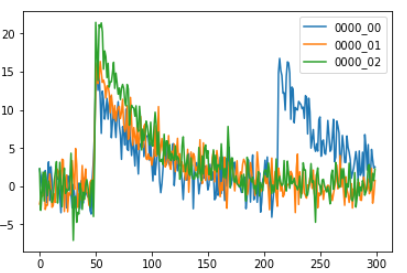
データ3つ分だけプロットしてみます。
50点目付近で最大波高値が得られるように掃き出してくれていました。

ヒストグラムの作成

最大波高値でヒストグラムを作成します。
ヒストグラムを作る際、横軸の刻み幅を決めなくてはなりません。
今回はSturgesの公式に従い、ビン数: k=1+Log2(n)としました。
注※np.histogramは度数(count)と同じ数だけの幅を返します。

.ipynb

bins = int(1+np.log2(pulse.shape[1]))#Sturgesの公式
count, level = np.histogram(pulse.max(),bins=bins)
level = np.array(list(map(lambda x:(level[x]+level[x+1])/2,range(level.size-1))))
#度数とサイズを揃える  
level = np.array(list(map(lambda x:(level[x]+level[x+1])/2,range(level.size-1))))
import matplotlib.pyplot as plt
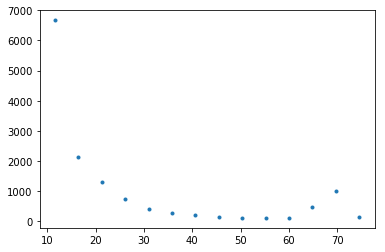
plt.plot(level,count,marker='.',linestyle='None')
plt.show()

右側にちょこっと山ができていました。50以降のデータ切り離して右側の山について再度分布を作ってみます。

.ipynb

mask = pulse.max()>50#bool値のアレイを作る
pulse = pulse.loc[:,mask]#パルスデータをマスキング

bins = int(1+np.log2(pulse.shape[1]))#Sturgesの公式
count, level = np.histogram(pulse.max(),bins=bins)
level = np.array(list(map(lambda x:(level[x]+level[x+1])/2,range(level.size-1))))
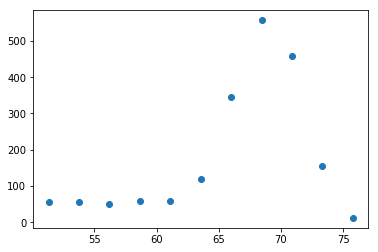
plt.plot(level,count,marker='o',linestyle='None')
plt.show()

正規分布っぽいものが現れました。

lmfitを使ってフィッティング

import~ の所を見て頂くとわかりますが、lmfitはいくつかのクラスオブジェクトを使ってフィッティングを行います。
フィッティング関数はガウス分布で、以下の通りです。ピークの中心は$\mu$、分布のバラつきは$\sigma$によって与えられます。ampは振幅項です。
$$f_{\left(x\right)}=\frac{amp}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{\left(x-\mu \right)^2}{2\sigma^2}\right)$$
まず、Modelクラスにフィットさせる関数を与えます。
次に、Parametersクラスを作成し、そこに初期値を与えます。
Modelクラスには.make_params()メソッドがあり、与えた関数の第二引数以降で勝手にParametersオブジェクト作ってくれます。

.ipynb

from lmfit import Model, Parameters, Parameter
def gaussian(x,amp,mu,sigma):
    out = amp / (sigma * np.sqrt(2 * np.pi)) * np.exp(-(x - mu)**2 /(2 * sigma**2))
    return out
model = Model(gaussian)#フィッティングする関数を代入、モデルオブジェクト作成
pars = model.make_params()#Parametersオブジェクト生成
pars

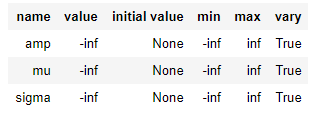
作ったParametersオブジェクトはParameterオブジェクトの集合になっています。それぞれのパラメータには辞書っぽくアクセスできるようになっています。そこから.setメソッドで
・初期値　value
・パラメータの上限・下限、max, min : -np.inf~np.inf　まで
・フィッティング前後で値を変化させるかどうか(拘束) vary=True or False
について、それぞれいじることができます。

.ipynb

pars['mu'].set(value=70)
pars['amp'].set(value=1)
pars['sigma'].set(value=1)
pars

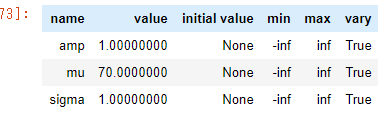
すごく大雑把ですが初期値を与えました。
パラメータを細かく設定できるうえにDataFrameライクなテーブルで表示される。クールだ・・・。

フィッティングを実行します

.ipynb

result = model.fit(data=count,params=pars,x=level)
result

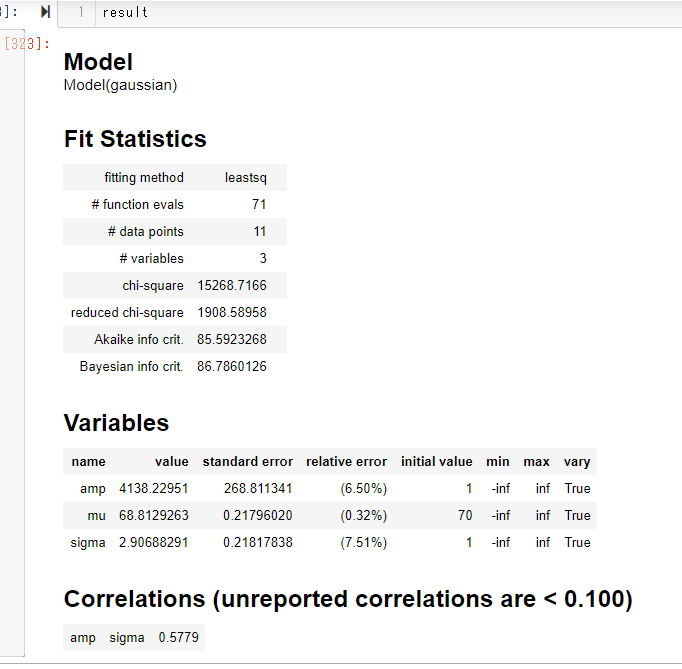
結果がこんな感じに表示されました。.fitを実行すると新たにModelResultオブジェクトが生成されるようです。
生成されたオブジェクトは.plot_fit()メソッドを持っていました。この機能で可視化します。

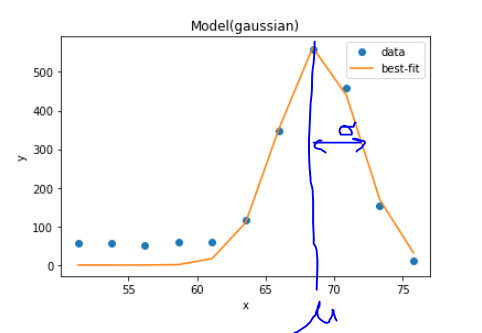
.best_valuesメソッドを使うことで、最適化されたパラメータを辞書型で取り出すことができます。

.ipynb

opt = result.best_values
opt['mu']/opt['sigma']

鋭さを$\frac{\mu}{\sigma}$で評価しました。23.67でした。

横軸の刻み幅を変えてみた

・Scottの公式
$$h = \frac{3.49\sigma}{ n^\frac{1}{3} }$$
で刻み幅を定義してみました。せっかくなので$\sigma$もフィッティングで求めたやつをつかいます。

.ipynb

h = 3.49 * opt['sigma'] / (pulse.shape[1] **(1/3))#Scottの公式
r = pulse.max().max()-pulse.max().min()
bins = int(r/h)

count, level = np.histogram(pulse.max(),bins=bins)
level = np.array(list(map(lambda x:(level[x]+level[x+1])/2,range(level.size-1))))
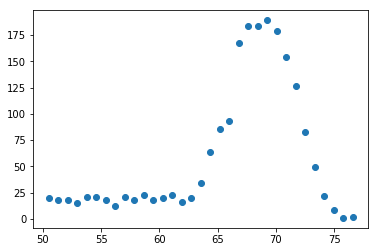
plt.plot(level,count,marker='o',linestyle='None')
plt.show()

刻み幅が狭くなって、その分度数の最大値が小さくなりましたが、分布の形は大丈夫そうです。
代入するdataとxの値だけ入れ替えて同様にフィッティング。

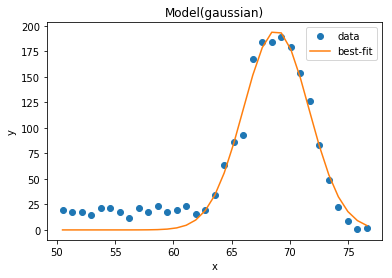
鋭さは・・・24.44。0.77だけ改善。

誤差に重み付けをしてみた

ここからが本件。

$\mu\pm\sigma$の範囲を強めに、かつ、63未満の重みを0にフィッティングしたいとのことでした。
.fit内のweightsオプションを指定することで重み付けができるみたいです。

.ipynb

s = (level>opt['mu']-opt['sigma']) * (level<opt['mu']+opt['sigma'])
weight = (np.ones(level.size) + 4*s)*(level>63)
result3 = model.fit(data=count,params=pars,x=level,weights=weight)

↓重み＆結果


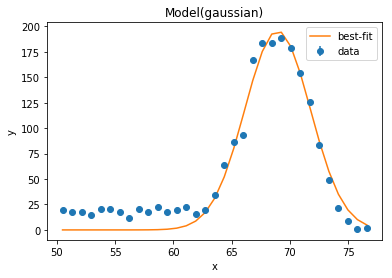
見た目あんまり変わっていませんが、よく見ると少しだけ下に引っ張られている気がします。
鋭さは・・・25.50。　0.06だけ更に鋭くなりました。

フィット後の点は、.best_fitメソッドを使うとarray型で呼び出すことができます。csvを作るときに便利でした。
無事、課題解決…

まとめ

今回はModel.make_params()でパラメータを自動生成しましたが、Parameters()で空のクラスを直接生成し、そこに.addメソッドで変数を追加していく方法もあります。

複数のオブジェクトを使ってフィッティングするので、最初は戸惑いました。どこにどのメソッドが対応しているのか、混乱しがちでした。しかし、使い慣れてくるとParameter(s)のありがたみを感じるかと思います。

lmfitを日本語で解説しているサイトが少なかったことがこの記事を書き始めたきっかけでもありました。もっといいライブラリがあるのでしょうか…？　ご教授いただければ幸いです。今後、後輩君が困らずに済むでしょう。
公式リファレンスを読みながらコードを書いたのは初めてでした（笑）。研究成果がかかっている分、やるしかない。

今後はもうちょっと生活に結び付きそうな技術を習得したいですし、持っている技術を様々な方面に活用できるようにもなりたいです。クリエイティブになりたい。

以上、python関連の進捗でした。教授に報告してもしょうがなかった(誰もpythonやってない)ので、この場を借りて報告致します。私のデータ解析を気長に待っていただいたこと、この点につきまして、教授には深く感謝を申し上げます。