はじめに
先日いつものようにtwitterを徘徊していたら、高校における物理の履修率が20%ほどに低下している旨のツイート)を見かけました。
確かに、物理という科目は難解な数式が並んでいるイメージを連想させてしまいがちです。しかし少なくとも高校物理の中心である古典力学は高度に体系化されており、その様子は非常に美しいものとなっています。今回は、数少ない基本法則から微分方程式を用いることであらゆる現象を再現できることをPythonを用いて実践してみます。物理屋だから言わせてもらうと、高校での物理履修率が90%からどんどん下がって20%とかになった時点で、モノ作りの国としては正直アウトなんですよね…日本病ですね。 https://t.co/JFrQXz5fbU
— 竹内薫 (@7takeuchi7) May 2, 2020
Pythonで微分方程式を解くために
まずは例として以下のような簡単な微分方程式を解きましょう。
\frac{dx}{dt} = at + b
ライブラリのimport
使用するライブラリはscipyで、その中のodeintを用います。odeというのもあるらしいですが、今回はそこまで複雑な演算は行わないのでodeintで十分です。以下のようにimportします。
from scipy.integrate import odeint
微分方程式の記述
equationという関数を作り、その中に微分方程式の右辺を書いていきます。第1変数に目的関数、第2変数に変数、それ以降は係数です。なお、第1変数(ここではx)はベクトルにもなり得ます。
def equation(x,t,a,b):
return a*t + b
微分方程式を解く
実際に解くのは簡単です。a,bに実際に数値を代入して解いてみましょう。
import numpy as np
t = np.arange(0,5,0.1) #0から5まで0.1刻みで解く
x0 = 0 #初期条件
a = 1
b = 2
x = odeint(equation,x0,t,args=(a,b))
odeintの第1変数が先ほど記述した微分方程式、第2変数が初期条件、第3変数が変数(タプル)です。
返り値はarrayで返ってきます。どのような結果になるかはご自身で確かめてみてください。
実際にシミュレーションしてみよう
ようやく本題です。今回は以下の2つを行います。
- モンキーハンティング
- バネの減衰振動・強制振動
モンキーハンティング
おそらく力学を学び始めた人が最初に感動するものがこれだと思います。それくらい超有名な問題です。
モンキーハンティングとは?
モンキーハンティングとは次のように説明されています1。
木の枝にぶら下がっている猿に狙いを定めて銃を撃つと、その音に驚いて手を離して落下した猿に必ず当たります。銃の弾は一直線に飛ぶわけではなく、重力によって少し下降します。それなのに必ず猿に命中するのです。このことをモンキーハンティングといいます。
もちろん条件がありまして、空気抵抗が無いことと、銃を撃つのと猿が手を放すのが同時(つまり音速は無限大*で、驚いてから手を放すまでのタイムラグも無い)ということです。
...なんとも残酷な話ではありますが、物理的な視点では面白いものになっています。
運動方程式の立式
弾丸とお猿さんの鉛直方向の位置をyとして立式してみます。正の向きは鉛直方向上向きです。
m\frac{d^2y}{dt^2} = -mg\\\
\therefore\frac{d^2y}{dt^2} = -g
Pythonで解くための変形
人間なら暗算で解けるくらいの微分方程式ですが、odeintは一階微分方程式しか解けません。ですから、面倒でも次のような形に変形してやらなくてはなりません。
\frac{dy}{dt} = v\\\
\frac{dv}{dt} = -g
2つの微分方程式が出てきました。果たしてこれらをそれぞれ解かなくてはならないのでしょうか。
これを無理やり1つの式にすると、
\frac{d}{dt} \left(\begin{array}{c}y \\ v\end{array}\right) = \left(\begin{array}{rr}0 & 1 \\ 0 & 0\end{array}\right)\left(\begin{array}{c}y \\ v\end{array}\right) + \left(\begin{array}{c}0 \\ -g\end{array}\right)
となります。
先ほど、odeintを用いた微分方程式の解き方を説明した際に目的関数はベクトルにもなり得ると説明しました。つまりyとvをlistにしてそれを目的関数としてやれば1つの式で解けることになるのです。
実装
では、実装していきましょう。
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
g = 9.8 #重力加速度[m/s^2]
L = 10 #弾丸の発射地点とお猿さんとの直線距離[m]
theta = np.pi/4 #弾丸の発射角度[rad]
v0 = 10 #弾丸の初速[10m/s]
interval = 10 #計算上の時間間隔[ms]
t = np.arange(0,L/v0,interval/1000)
y0 = [[0,v0*np.sin(theta)], #弾丸の初期条件(y,v)
[L*np.sin(theta),0]] #弾丸の初期条件(y,v)
def equation(y,t,g):
ret = [y[1],-1*g] #上の式の右辺そのまま
return ret
y1 = odeint(equation,y0[0],t,args=(g,))
y2 = odeint(equation,y0[1],t,args=(g,))
y1とy2の結果は次のようになります。
y1:
# [弾丸の位置 弾丸の鉛直方向の速度]
[[ 0. 7.07106781]
[ 0.07022068 6.97306781]
[ 0.13946136 6.87506781]
...
]
y2:
# [お猿さんの位置 お猿さんの鉛直方向の速度]
[[ 7.07106781 0. ]
[ 7.07057781 -0.098 ]
[ 7.06910781 -0.196 ]
...
]
このままでは使いにくいので転置しておきましょう。
y1.T:
[[ 0. 0.07022068 0.13946136 0.20772203 0.27500271 0.34130339
0.40662407 0.47096475 0.53432542 0.5967061 0.65810678 0.71852746
...
2.2723851 2.24852578 2.22368646 2.19786713]
[ 7.07106781 6.97306781 6.87506781 6.77706781 6.67906781 6.58106781
...
-1.74893219 -1.84693219 -1.94493219 -2.04293219 -2.14093219 -2.23893219
-2.33693219 -2.43493219 -2.53293219 -2.63093219]]
y2.T:
[[ 7.07106781 7.07057781 7.06910781 7.06665781 7.06322781 7.05881781
7.05342781 7.04705781 7.03970781 7.03137781 7.02206781 7.01177781
...
2.55522781 2.46065781 2.36510781 2.26857781]
[ 0. -0.098 -0.196 -0.294 -0.392 -0.49
...
-8.232 -8.33 -8.428 -8.526 -8.624 -8.722
-8.82 -8.918 -9.016 -9.114 -9.212 -9.31
-9.408 -9.506 -9.604 -9.702 ]]
きちんと演算できたようです。
可視化
可視化にはMatplotlibを使うので、せっかくだからアニメーションを使いましょう。今回はFuncAnimationを使用します。
仕組みとしては、update_anim関数で一定間隔でデータをplotして更新していく仕組みです。
fig,ax = plt.subplots()
obj1, = ax.plot([],[],'o')
obj2, = ax.plot([],[],'^')
ax.set_xlim(0,L*np.cos(theta)*1.2)
ax.set_ylim(min(y1.T[0])*1.2,L*np.sin(theta)*1.2)
ax.set_aspect('equal')
ax.set_title('v0={},theta={}°'.format(v0,theta*180/np.pi))
def update_anim(frame_num):
obj1.set_data(v0*np.cos(theta)*t[frame_num],y1.T[0][frame_num]) #(水平方向の速度×経過時間, 鉛直方向の位置)
obj2.set_data(L*np.cos(theta),y2.T[0][frame_num])
return obj1, obj2,
anim = FuncAnimation(fig,update_anim,frames=np.arange(0,len(t)),interval=interval,blit=True,repeat=True)
plt.show()
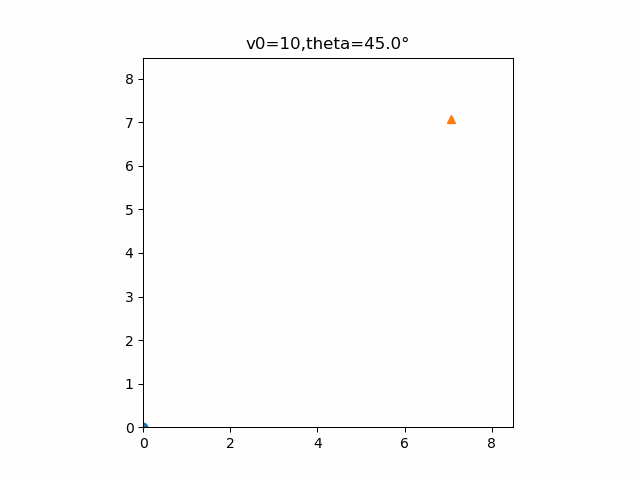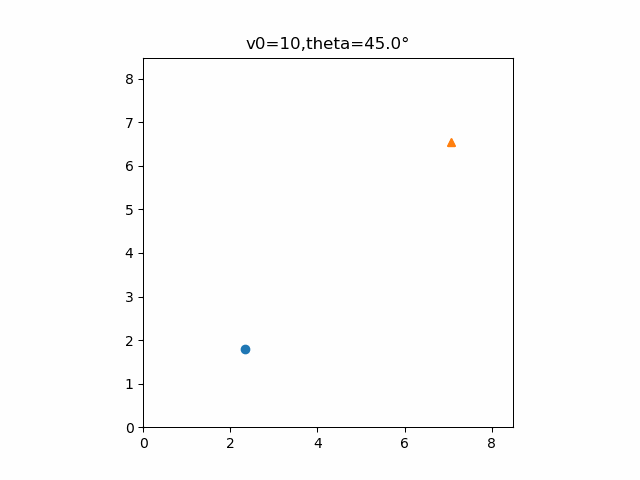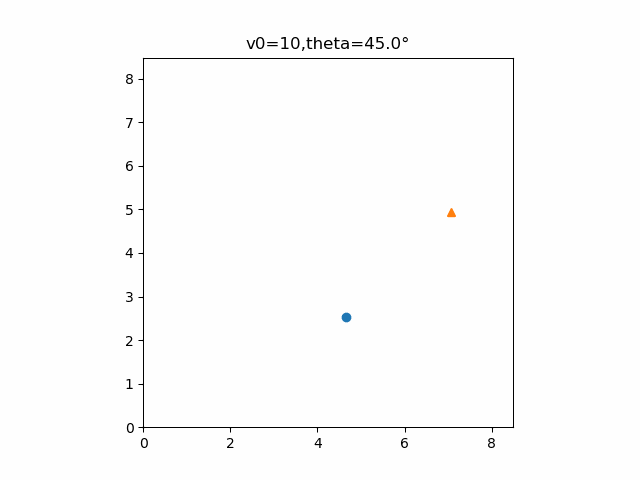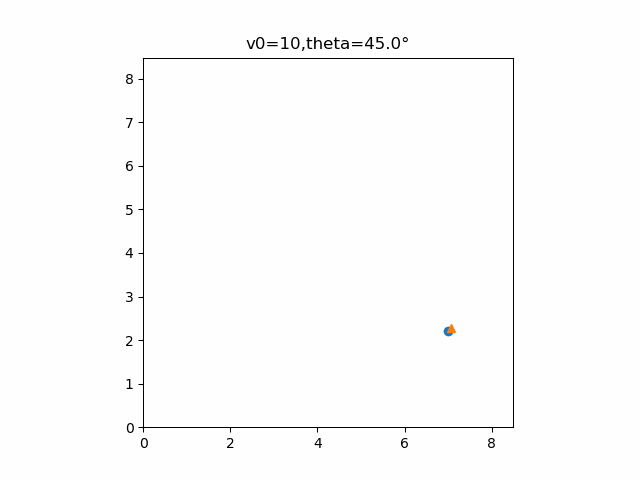
書き出すとゆっくりになってしまいましたが、実際は等倍速で見ることができます。確かに2物体は衝突していることが分かります。
バネの減衰振動・強制振動
単なる放物運動だけではつまらないので、バネの運動を紹介します。
運動方程式の立式
バネの外力を含めた運動は次のように記述されます。
m\frac{d^2x}{dt^2} = -kx+fcos(\omega_0t)-a\frac{dx}{dt}\\\
\therefore \frac{d^2x}{dt^2} = -\omega^2x+\frac{f}{m}cos(\omega_0t)-\frac{a}{m}\frac{dx}{dt} \\\
\left(\omega=\sqrt{\frac{k}{m}}\right)
ここでfは外力、aは減衰係数です。これも同様に2つの式に分解します。
\frac{dx}{dt} = v\\\
\frac{dv}{dt} = -\omega^2x+\frac{f}{m}cos(\omega_0t)-\frac{a}{m}v
今回も同様にしてvとxのlistとして目的関数をまとめましょう。
実装
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
interval = 10 #計算上の時間間隔[ms]
t = np.arange(0,20,interval/1000)
k = 50 #バネ定数[N/m]
m = 0.1 #重りの質量[kg]
w = np.sqrt(k/m)
w0 = np.sqrt(k/m) #今回は共振を再現するためにw=w0
x0 = [0,-1*w**2*0.2] #初期条件(v,x). つまり重りを釣り合いの位置から20cm離れたところからスタート
f = 0 #外力の大きさ
a = 0 #減衰係数
def equation(x,t,w,f,m,w0,a):
ret = [-1*w**2 * x[1] + f/m*np.cos(w0*t) - a/m*x[0], x[0]]
return ret
x = odeint(equation,x0,t,args=(w,f,m,w0,a))
xの中身については先ほどとほとんど同じですので割愛します。
可視化
先ほどと同じ方法でアニメーションにします。
fig,ax = plt.subplots()
image, = ax.plot([],[], 'o-', lw=2)
ax.set_xlim(min(x.T[1]*(-1)*m/k)*1.2,max(x.T[1]*(-1)*m/k)*1.2)
ax.set_ylim(-0.1,0.1)
ax.set_title('f={},a={}'.format(f,a))
def update_anim(frame_num):
image.set_data([x.T[1][frame_num]*(-1)*m/k,0],[0,0])
return image,
anim = FuncAnimation(fig, update_anim,frames=np.arange(0, len(t)),interval=interval ,blit=True)
plt.show()
終わりに
以上のようにして運動方程式から様々な現象をシミュレーションできました。
他にも雨粒の終端速度などを数値を変えて遊んでみると面白いかもしれません。
参考文献
Pythonで運動方程式を解く(odeint)
scipy で2階常微分方程式の数値解を求める