この記事は
python(正確にはscipy)のodeintというライブラリを使って運動方程式を解きます。anacondaで入れたpython3.6.3を使っています。
運動方程式(二階微分方程式)を解いていますが、一階の微分方程式など他の微分方程式にも応用可能です。
Pythonで運動方程式を解きたい
人生とは
簡単な運動方程式を解きたい場合が人生の中では出てくる。
特に、解いて運動の様子をplotしたい場合がある。
その時人はどうするか
今回はpythonのライブラリ"odeint"を用いて楽してプロットすることを目的にする。
odeint
おでんitに見える。
ODE integralのことだと思う。
ODE=Ordinary Differential Equation (常微分方程式)
公式reference
https://docs.scipy.org/doc/scipy/reference/generated/scipy.integrate.odeint.html
odeというライブラリもある
https://docs.scipy.org/doc/scipy/reference/generated/scipy.integrate.ode.html
調べるとどうやらもっと新しいpackage"solve_ivp"があるらしく、こちらが推奨されている。いつかこれについても記事を書きたい。
https://docs.scipy.org/doc/scipy/reference/generated/scipy.integrate.solve_ivp.html#scipy.integrate.solve_ivp
ちなみにodeintと、他二つ(ode, solve_ivp)では引数の順番が違うというエグい仕様になっている。混同しないように気をつけよう。
今回解きたい運動方程式
運動方程式なら何でも良いのだが、今回は簡単な投げ上げを解く。
m\ddot y=-rv+mg
odeintで二階微分方程式を特には、二つの一階微分に直す必要がある。例えば今回の場合は
\dot y=v \\
m\dot v=-rv+mg
という式を実際にはodeintで解く。
コード
全体の流れ
コードの流れは以下の通り
- 必要なライブラリを読み込む
- 解きたい微分方程式を記述する
- 初期条件等を決めて方程式をodeintに解いてもらう
- 結果を描く
準備
まず、色々ライブラリを入れる。
import numpy as np #numpy
from scipy.integrate import odeint #odeint
import matplotlib.pyplot as plt #to draw graphs
微分方程式を書く
そして、微分方程式を定義する。
空気抵抗r,質点の質量mは次のステップで定義される。
重力定数gは変更しないので今回はここで定義している。
def func(s, t, r, m):
y, v = s #sは変数yとvの組
g=9.80665 #m/s^2
dsdt = [v, (-r*v-m*g)/m]
return dsdt
初期条件を決めて、微分方程式を解いてもらう
空気抵抗r,質量mを決め、初期条件を決めて微分方程式を解く。
sol = odeint(func, y0, t, args=(r,m))の最後の引数について、一点注意。
args=(r,m)のようにリストを渡すので、引数が一つの場合はargs=(r,)のようにしなければならない。今回は困らないが、他の運動方程式を解く場合には注意。
r=12
m=100
y0 = [0,10]#位置0から初速10で投げ上げ
t = np.linspace(0, 7, 201)#時刻0から7まで、201step刻みで計算する
sol = odeint(func, y0, t, args=(r,m))
結果を図に描く
結果を可視化してみよう。
plt.plot(t, sol[:, 0], 'b', label='y')#yについてplot
plt.plot(t, sol[:, 1], 'g', label='v')#vについてplot
plt.legend(loc='best')#レジェンドを付ける
plt.xlabel('t')
plt.grid()#格子を付ける
plt.show()
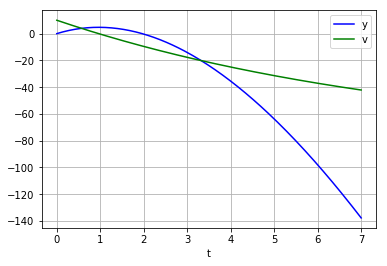
そうするとこんな図が得られるはず。
この次は
最初はtを0から100までなどと変更して終端速度を確認したり、あるいは斜めに投げ上げた場合の問題を解いたりするのがコードを理解する良い練習問題になると思う。