はじめに
こちらの本を読みつつ、演習・実験を試してみます。
「『クラウド量子計算入門』の演習を行う (2 パウリゲートの量子実験) - Qiita」の続き。
3 アダマールゲートの量子実験
3.1 アダマール変換とは
3.1.2 アダマール変換
演習 3-1
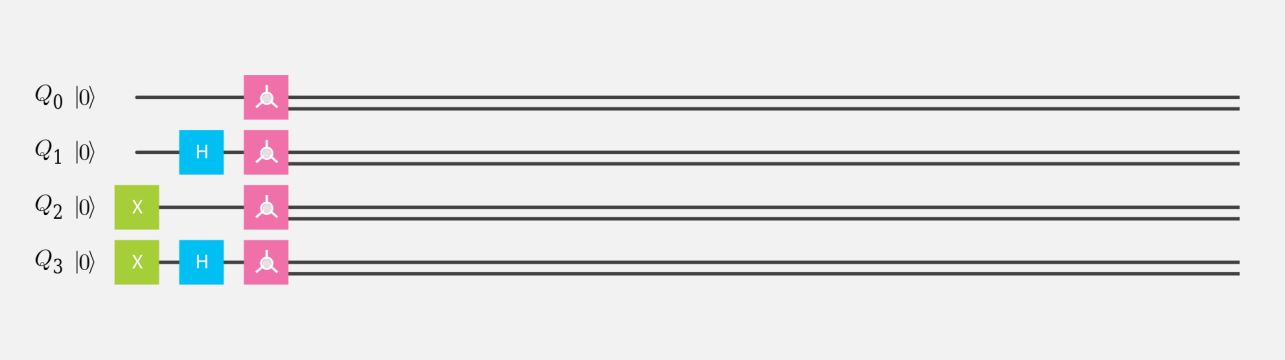
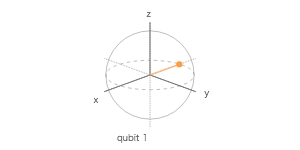
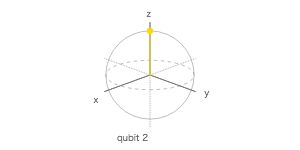
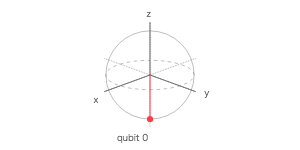
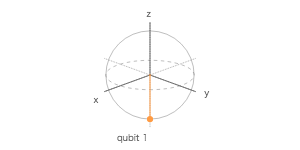
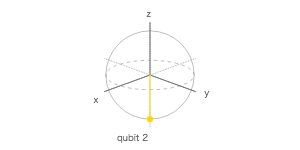
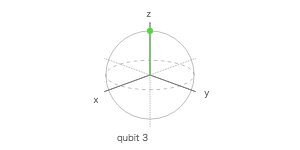
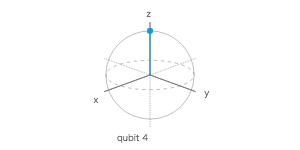
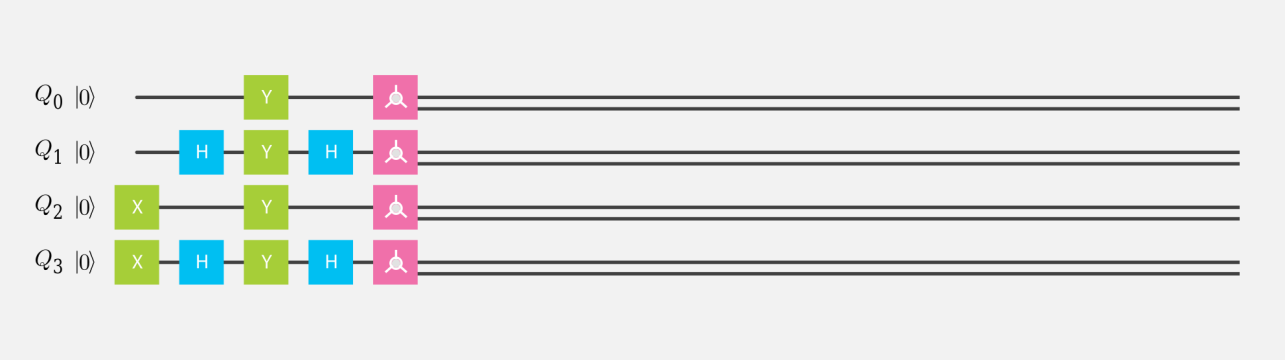
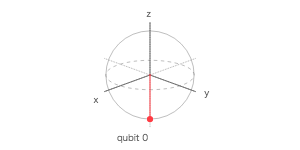
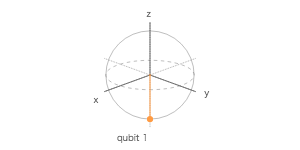
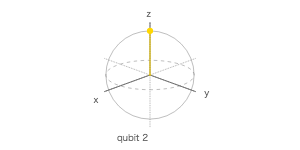
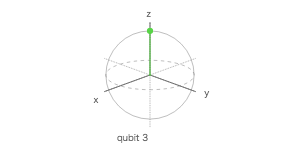
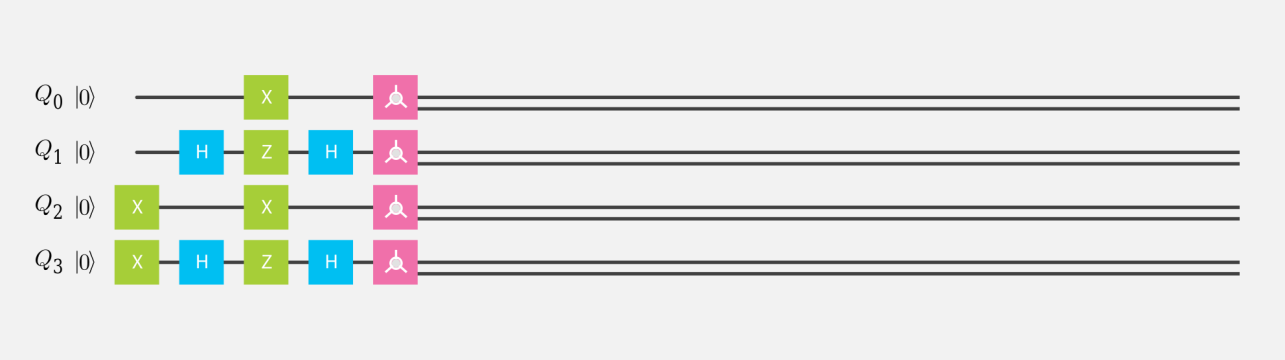
量子シミュレータで 4 量子ビットを使って、$ |0\rangle $、$ H|0\rangle $、$ |1\rangle $、$ H|1\rangle $ を計算する量子回路を作成し、ブロッホ測定の 3 次元表示で調べてみよ。
ブロッホ測定
量子回路
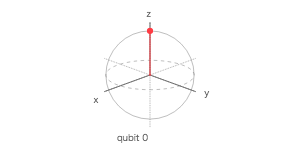
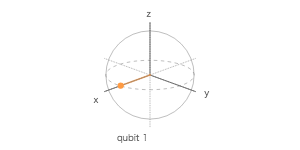
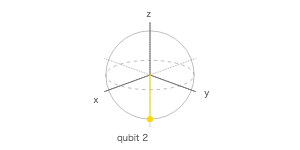
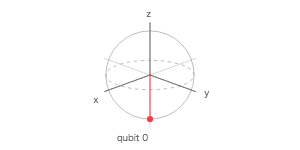
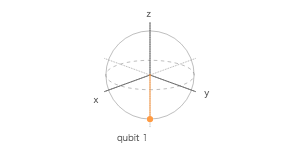
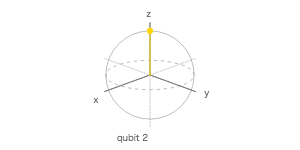
ブロッホ球
| Shots | Qubit | X | Y | Z |
|---|---|---|---|---|
| 1 | Q0 | 0 | 0 | 1 |
| 1 | Q1 | 1 | 0 | 0 |
| 1 | Q2 | 0 | 0 | -1 |
| 1 | Q3 | -1 | 0 | 0 |
3.1.3 アダマール変換による均等な重ね合わせ状態の生成
演習 3-2
量子シミュレータで 5 量子ビット用いて、均等な重ね合わせ状態を生成して、各基準基底での確率が理論と一致しているか確かめよ。
行列計算
|x\rangle
=
\otimes_{i=1}^{5} \biggl( \frac{|0\rangle+|1\rangle}{\sqrt{2}} \biggl)
=
\biggl( \frac{1}{\sqrt{2}} \biggl)^5 \bigr( |0\rangle+|1\rangle+,...,+|2^5-1\rangle \bigr)
=
\biggl( \frac{1}{\sqrt{2}} \biggl)^5 \, \sum_{n=0}^{2^5-1} |n\rangle
これで大丈夫だと思うのだけど、まだよくわからない。
確率振幅は 1/5、観測確率は 1/32 = 0.03125 となる。
標準基底測定
量子回路
実行結果
| Shots | Value | Probability | Qubits Measured |
|---|---|---|---|
| 1 | 0 | 0.03125 | 0,1,2,3,4 |
| 1 | 1 | 0.03125 | 0,1,2,3,4 |
| 1 | 10 | 0.03125 | 0,1,2,3,4 |
| 1 | 11 | 0.03125 | 0,1,2,3,4 |
| 1 | 100 | 0.03125 | 0,1,2,3,4 |
| 1 | 101 | 0.03125 | 0,1,2,3,4 |
| 1 | 110 | 0.03125 | 0,1,2,3,4 |
| 1 | 111 | 0.03125 | 0,1,2,3,4 |
| 1 | 1000 | 0.03125 | 0,1,2,3,4 |
| 1 | 1001 | 0.03125 | 0,1,2,3,4 |
| 1 | 1010 | 0.03125 | 0,1,2,3,4 |
| 1 | 1011 | 0.03125 | 0,1,2,3,4 |
| 1 | 1100 | 0.03125 | 0,1,2,3,4 |
| 1 | 1101 | 0.03125 | 0,1,2,3,4 |
| 1 | 1110 | 0.03125 | 0,1,2,3,4 |
| 1 | 1111 | 0.03125 | 0,1,2,3,4 |
| 1 | 10000 | 0.03125 | 0,1,2,3,4 |
| 1 | 10001 | 0.03125 | 0,1,2,3,4 |
| 1 | 10010 | 0.03125 | 0,1,2,3,4 |
| 1 | 10011 | 0.03125 | 0,1,2,3,4 |
| 1 | 10100 | 0.03125 | 0,1,2,3,4 |
| 1 | 10101 | 0.03125 | 0,1,2,3,4 |
| 1 | 10110 | 0.03125 | 0,1,2,3,4 |
| 1 | 10111 | 0.03125 | 0,1,2,3,4 |
| 1 | 11000 | 0.03125 | 0,1,2,3,4 |
| 1 | 11001 | 0.03125 | 0,1,2,3,4 |
| 1 | 11010 | 0.03125 | 0,1,2,3,4 |
| 1 | 11011 | 0.03125 | 0,1,2,3,4 |
| 1 | 11100 | 0.03125 | 0,1,2,3,4 |
| 1 | 11101 | 0.03125 | 0,1,2,3,4 |
| 1 | 11110 | 0.03125 | 0,1,2,3,4 |
| 1 | 11111 | 0.03125 | 0,1,2,3,4 |
3.2 アダマール演算による量子シミュレータ実験
3.2.2 アダマール演算によるパウリ演算の変換
演習 3-3
3 量子ビットの量子シミュレータを使って、$ H|1\rangle $、$ ZH|1\rangle $、$ HZH|1\rangle $ を確かめる量子回路を作成し、行列計算と一致しているか確かめよ。測定はブロッホ測定の 3 次元表示で確かめよ。
行列計算
ZH|1\rangle
=
\frac{1}{\sqrt{2}}
\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}
\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}
\begin{bmatrix} 0 \\ 1 \end{bmatrix}
=
\frac{|0\rangle + |1\rangle}{\sqrt{2}}
- $ HZH|1\rangle $ は演習 3-4 にもあるのでそちらで。
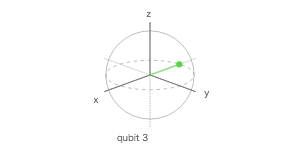
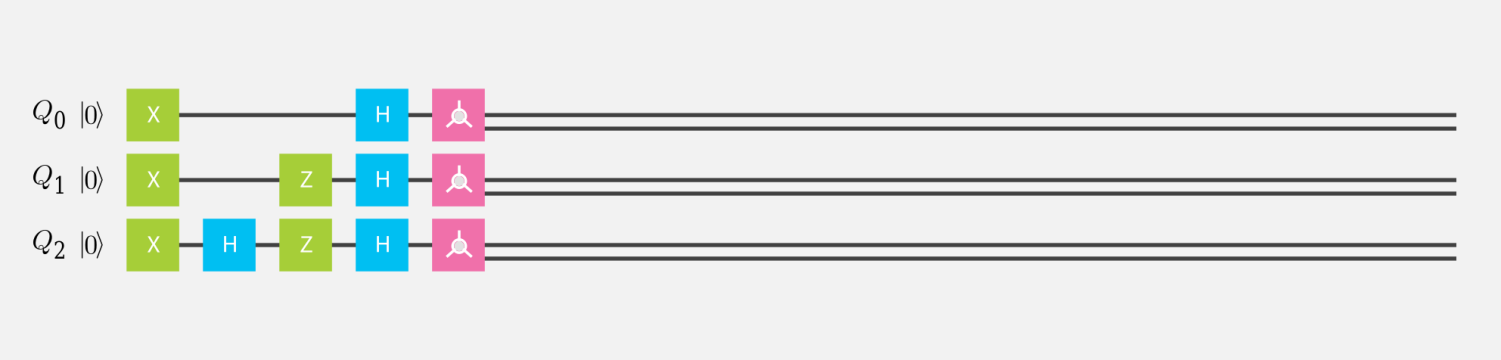
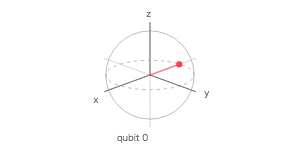
ブロッホ測定
量子回路
ブロッホ球
| Shots | Qubit | X | Y | Z |
|---|---|---|---|---|
| 1 | Q0 | -1 | 0 | 0 |
| 1 | Q1 | -1 | 0 | 0 |
| 1 | Q2 | 0 | 0 | 1 |
演習 3-4
3 量子ビットの量子シミュレータを使って、$ |1\rangle $、$ HH|1\rangle $、$ HXH|1\rangle $、$ HYH|1\rangle $、$ HZH|1\rangle $ を確かめる量子回路を作成し、行列計算と一致しているか確かめよ。測定はブロッホ測定の 3 次元表示で確かめよ。
これは 5 量子ビットの間違いかな?
行列計算
HH|1\rangle
=
\frac{1}{2} \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}
\begin{bmatrix} 1 \\ -1 \end{bmatrix}
=
\begin{bmatrix} 0 \\ 1 \end{bmatrix}
=
|1\rangle
HXH|1\rangle
=
\frac{1}{2}
\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}
\begin{bmatrix} -1 \\ 1 \end{bmatrix}
=
- \begin{bmatrix} 0 \\ 1 \end{bmatrix}
=
-|1\rangle
HYH|1\rangle
=
\frac{1}{2}
\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}
\begin{bmatrix} i \\ i \end{bmatrix}
=
i\begin{bmatrix} 1 \\ 0 \end{bmatrix}
=
i|0\rangle
HZH|1\rangle
=
\frac{1}{2}
\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}
\begin{bmatrix} 1 \\ 1 \end{bmatrix}
=
\begin{bmatrix} 1 \\ 0 \end{bmatrix}
=
|0\rangle
ブロッホ測定
量子回路
ブロッホ球
| Shots | Qubit | X | Y | Z |
|---|---|---|---|---|
| 1 | Q0 | 0 | 0 | -1 |
| 1 | Q1 | 0 | 0 | -1 |
| 1 | Q2 | 0 | 0 | -1 |
| 1 | Q3 | 0 | 0 | 1 |
| 1 | Q4 | 0 | 0 | 1 |
演習 3-5
量子シミュレータで 4 量子ビット用いて、$ HYH=-Y $ を確かめる量子回路を作成せよ。グローバルな位相因子は無視してよい。
ブロッホ測定
量子回路
ブロッホ球
| Shots | Qubit | X | Y | Z |
|---|---|---|---|---|
| 1 | Q0 | 0 | 0 | -1 |
| 1 | Q1 | 0 | 0 | -1 |
| 1 | Q2 | 0 | 0 | 1 |
| 1 | Q3 | 0 | 0 | 1 |
演習 3-6
量子シミュレータで 4 量子ビット用いて、$ HZH=X $ を確かめる量子回路を作成せよ。
ブロッホ測定
量子回路
ブロッホ球
| Shots | Qubit | X | Y | Z |
|---|---|---|---|---|
| 1 | Q0 | 0 | 0 | -1 |
| 1 | Q1 | 0 | 0 | -1 |
| 1 | Q2 | 0 | 0 | 1 |
| 1 | Q3 | 0 | 0 | 1 |