回帰分析
単回帰
単回帰:導入
非常に単純な式。モデル式は、 $\hat{y} = ax + b + \epsilon$
($\epsilon$は誤差項。本稿ではあまり意味を持たないので、今後は省略する)
データは(x, y)の形(説明変数、目的変数ともに1次元という意味)。
単回帰のイメージ図
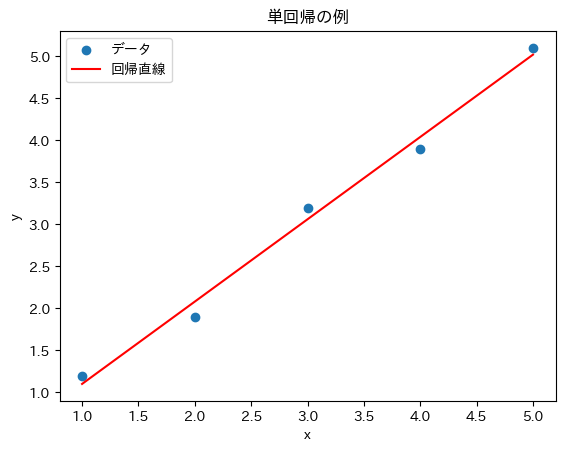単回帰:具体的な条件
データのペアx, yが複数個(n個のペア)あるとする。
Data = \{(x_1, y_1), (x_2, y_2), (x_3, y_3), \cdots , (x_k, y_k), \cdots , (x_n, y_n)\}
この各x,yとの値と、$\hat{y} = ax + b$ との差が最も小さくなるように係数a,bを求めるのが単回帰。
k番目のデータペア$(x_k, y_k)$ と $\hat{y} = ax + b$ との差は、
\begin{align}
residual^2 &= (y_k - \hat{y_k})^2 \\
&= \big(y_k - (ax_k + b)\big)^2
\end{align}
ここで、$x_k, y_k$ はともに観測された具体値である(既知の値)。
求めるのは、a,bの値。
「最小二乗法」で解く。つまり、以下の通り。
全$n$個のペア $Data=\{\cdots\}$ について上記各「残差2乗」の総和をとり、この値を最小化する。
単回帰:解き方
最小二乗法。全データの残差の2乗和を最小化する。
残差二乗和を微分して0になる点が、二乗和最小値。
全$n$個のデータの残差2乗和を$E$と記述すると、
\displaylines{
E = \sum_{k=1}^n\big(y_k - (ax_k + b)\big)^2 \\
min(E) = min\Big(\sum_{k=1}^n\big(y_k - (ax_k + b)\big)^2 \Big)
}
2乗和なので、2次関数の最小値を求める問題と同義。これは微分が0になる点が最小。
最小を与えるa、bを求めることが、単回帰を解くことになる。
以下は具体的な計算
先に残差2乗和の式を展開する。E = \sum_{k=1}^n(y_k^2 + (ax_k+b)^2 - 2 y_k(ax_k+b))
微分=0なので、
\left\{
\begin{array}{}
\frac{\partial{E}}{\partial{a}} = 0 \\
\frac{\partial{E}}{\partial{a}} = 0 \\
\end{array}
\right\} \\
単純にモデル式を代入し、微分を具体的に計算
\left\{
\begin{array}{}
\frac{\partial{E}}{\partial{a}} = \sum_{k=1}^n(2ax_k^2 + 2bx_k - 2x_ky_k) = 0 \\
\frac{\partial{E}}{\partial{a}} = \sum_{k=1}^n(2ax_k+2b-2y_k) = 0 \\
\end{array}
\right\}
式を整理する。両辺$2$で割り、a,bを含まない項を右辺に移項。
\left\{
\begin{array}{}
a\sum x_k^2 + b\sum x_k = \sum x_ky_k \\
a \sum x_k + nb = \sum y_k \\
\end{array}
\right\}
\tag{ $\cdots$ 1.1}
連立方程式を解く。下側の式からbについて簡単にまとめられるので、このbを上側の式に代入し、
最後にa,b両方についてまとめる
\begin{align}
& b = \frac{1}{n}(\sum y_k - a\sum x_k) \\
& a\sum x_k^2 + \frac{1}{n}(\sum y_k\sum x_k - a(\sum x_k)^2) = \sum x_ky_k \\
& \Leftrightarrow \\
& a (n \sum x_k^2 - (\sum x_k)^2) = n\sum x_ky_k - \sum x_k \sum y_k \\
a &= \frac{n\sum x_ky_k - \sum x_k \sum y_k}{n \sum x_k^2 - (\sum x_k)^2} \\
b &= \frac{1}{n}(\sum y_k - \sum x_k\frac{n\sum x_ky_k - \sum x_k \sum y_k}{n \sum x_k^2 - (\sum x_k)^2}) \\
&= \frac{1}{n}(\frac{\sum y_k(n \sum x_k^2 - (\sum x_k)^2)}{n \sum x_k^2 - (\sum x_k)^2} - \frac{n\sum x_k\sum x_ky_k - (\sum x_k)^2 \sum y_k}{n \sum x_k^2 - (\sum x_k)^2}) \\
&= \frac{1}{n}\frac{n\sum x_k^2 \sum y_k - n\sum x_k \sum x_k y_k}{n \sum x_k^2 - (\sum x_k)^2} \\
&= \frac{\sum x_k^2 \sum y_k - \sum x_k \sum x_k y_k}{n \sum x_k^2 - (\sum x_k)^2}
\end{align}
結果、
\begin{align}
a &= \frac{n\sum x_ky_k - \sum x_k \sum y_k}{n \sum x_k^2 - (\sum x_k)^2} \\
b &= \frac{\sum x_k^2 \sum y_k - \sum x_k \sum x_k y_k}{n \sum x_k^2 - (\sum x_k)^2}
\end{align}
各観測データの総和などの計算から係数a、bを求めることができる。
単回帰:行列で楽に解く
微分して0になる、という連立方程式をまとめた、式1.1は以下であった
\left\{
\begin{array}{}
a\sum x_k^2 + b\sum x_k = \sum x_ky_k \\
a \sum x_k + nb = \sum y_k \\
\end{array}
\right\}
\tag{ $\cdots$ 1.1}
これを行列を用いて書くと、以下のように表現できる。
\begin{pmatrix}
\sum x_k^2 & \sum x_k \\
\sum x_k & n
\end{pmatrix}
\begin{pmatrix}
a \\
b
\end{pmatrix}
=
\begin{pmatrix}
\sum x_ky_k \\
\sum y_k
\end{pmatrix}
2x2の行列なので、逆行列は簡単に計算できる。
\begin{pmatrix}
A & B \\
C & D
\end{pmatrix}
^{-1} = \frac{1}{AD - BC}
\begin{pmatrix}
D & -B \\
-C & A
\end{pmatrix}
見た目がすっきりする。
具体値を計算するときにも、各$\sum x_k^2$などを個別に計算して行列式の形で計算すると良いので楽。
まとめ:モデル式と計算
モデル式:
\begin{align}
y &= ax+b+\epsilon \newline
\mathbf{\hat{y}} &= \begin{pmatrix}x_1 & 1 \\ x_2 & 1 \\ x_3 & 1 \\ \vdots \\ x_m & 1 \end{pmatrix} \begin{pmatrix}a \\ b\end{pmatrix}
\\
\mathbf{\hat{y}} &= \mathbf{X}\mathbf{w}
\end{align}
※bを反映するために行列の2列目に1を置いている
計算:
\begin{align}
\begin{pmatrix}
\sum x_k^2 & \sum x_k \\
\sum x_k & n
\end{pmatrix}
\begin{pmatrix}
a \\
b
\end{pmatrix}
&=
\begin{pmatrix}
\sum x_ky_k \\
\sum y_k
\end{pmatrix}
\\
\mathbf{X}^T\mathbf{X} \mathbf{w} &= \mathbf{X}\mathbf{y}
\end{align}
これを$\mathbf{w} = (a,b)^T$について解く
\mathbf{w} = (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}\mathbf{y}
重回帰
重回帰:導入
基本は単回帰と同じ。説明変数 x が、多次元になったもの。
(知りたい y がたくさんの要素の影響を受ける。xの次元数は、影響を与える因子の個数のこと)
重回帰:具体的な条件
データのペア$\mathbf{x}$, yが複数個(n個のペア)あるとする。
$\mathbf{x}$ は、m次元のベクトルとする
\mathbf{x}^T = \{x_1, x_2, \cdots , x_m\}
(一般にデータのベクトル(説明変数の次元数を持つベクトル)は縦ベクトルで書かれるため、転置$^T$をつけた)
単回帰はxは1次元であったのに対し、重回帰では$\mathbf{x}$がm次元という点が異なる。
逆に言えば違いはこれだけ。
単回帰と同じように残差2乗和の最小化を考えることで重回帰を解く。
残差を計算するための式($\hat{y}$の形)を以下のように定める。
\hat{y} = w_0 + w_1x_1 + w_2x_2 + \cdots + w_mx_m
$w_0$ は切片に相当し、{$w_1,w_2,\cdots,w_m$} はそれぞれ説明変数 {$x_1,x_2,\cdots,x_m$} に対応する係数。
k番目のデータペア$(x_k, y_k)$ と 予測モデル式 $\hat{y} = w_0 + w_1x_1 + w_2x_2 + \cdots + w_mx_m$ との差は、
\begin{align}
residual^2 &= (y_k - \hat{y_k})^2 \\
&= \big(y_k - (w_0 + w_1x_1 + w_2x_2 + \cdots + w_mx_m)_k\big)^2
\end{align}
求めるのは、各 {$w_0, w_1,w_2,\cdots,w_m$} の値。
「最小二乗法」で解く。単回帰と同じ。
全$n$個のペア $Data=\{\cdots\}$ について、残差2乗和を最小化する。
重回帰:ベクトル表現、行列表現
重回帰では項が多いので見易い書き方にしたい。これにベクトル表現を用いる(追って行列表現になる)
係数ベクトルを $\mathbf{w}$ ,説明変数ベクトルを $\mathbf{x}$ とする。
\begin{align}
\mathbf{w} &= \{w_0, w_1, w_2,\cdots,w_m\} \\
\mathbf{x} &= \{1, x_1, x_2,\cdots,x_m\} \\
\end{align}
$\mathbf{w}$ は切片項(つまり説明変数$\mathbf{x}$に関係ない項)があるので、辻褄合わせのために$\mathbf{x}$ の最初の要素に1を入れている。
すると、$\hat{y} = w_0 + w_1x_1 + w_2x_2 + \cdots + w_mx_m$ の右辺が簡略化でき、以下の記法となる。
\hat{y} = \mathbf{w}^T \mathbf{x}
2つのベクトルの内積で表現。内積は同じ要素番号同士を掛けて和を取るので、元の式に合致。
$\mathbf{w}^T \mathbf{x} = \mathbf{x}^T \mathbf{w}$ なので、次の話のために以下の記法としておく。
\begin{align}
\hat{y} &= \mathbf{x}^T \mathbf{w} \\
&= \begin{pmatrix}1 & x_1 & x_2 & \cdots & x_m \end{pmatrix}
\begin{pmatrix} w_0 \\ w_1 \\ w_2 \\ \vdots \\ w_m \end{pmatrix}
\end{align}
ところで、データ $\mathbf{x}$ は、n個のデータを取得すると、n個のデータセットになるのでその種類(セット数)はn個になる。
(係数である $\mathbf{w}$ はデータの個数に依らず一意の値を取るので、1セットのみでOK)
これまでは、データセット番号をkとして、$\sum_{k=1}^n()$ などの記法でN個のデータセットの計算を表現していた。
実は説明変数を行列形式で記載すると個の記法も簡略化できる。
説明変数 $\mathbf{x}$ を行列 $\mathbf{X}$ で表現する。
\mathbf{X} =
\begin{pmatrix}
1 & x_{11} & x_{12} & \cdots & x{_1m} \\
1 & x_{21} & x_{22} & \cdots & x{_2m} \\
\vdots & & \ddots & & \vdots \\
1 & x_{n1} & x_{n2} & \cdots & x{_nm} \\
\end{pmatrix}
すると、データをn個取った時のモデル式は、$\mathbf{\hat{y}}^T = {\hat{y_1}, \hat{y_2}, \cdots, \hat{y_n}}$ として、
\mathbf{\hat{y}}^T = \mathbf{X} \mathbf{w}
と書くだけで全ての情報を包括して表現できて便利。
このときの$\mathbf{X}$を計画行列と呼ぶ。
実験計画において、度の説明変数を使うか?交互作用や多項式項を$x_i$として使うか?など、$\hat{y}$を推定するために「計画する」ものなので、「計画行列」と呼ばれている。
計画行列次第で重回帰の予測性能が決まる。
さらに、前述の通り、内積は同じ要素同士の掛け算の和であったので、$\sum_{k=1}^n$ のような総和$\sum$も省ける。
単回帰の時、全n個のデータの残差2乗和を$\mathbf{E}$として、
\mathbf{E} = \sum_{k=1}^n\big(y_k - (ax_k + b)\big)^2
と書いていた。これを重回帰のようにn×m次元の説明変数$\mathbf{x}$やm次元の$\mathbf{w}$などを用いて書くと大変煩雑で理解しにくいが、行列を用いて書くと重回帰の残差2乗和の式は以下式に落ち着く。
\begin{align}
\mathbf{E} &= \sum_{k=1}^n\big(y_k - \hat{y_k}\big)^2
= \sum_{k=1}^n\big(y_k - \mathbf{x}_k^T\mathbf{w}_k\big)^2 \\
&= (\mathbf{y} - \mathbf{X} \mathbf{w})^T(\mathbf{y} - \mathbf{X} \mathbf{w})
\end{align}
見通しが良い。
重回帰:解き方
残差2乗和を最小化する。
残差2乗和:
\begin{align}
\mathbf{E} &= \sum_{k=1}^n\big(y_k - \hat{y_k}\big)^2
= \sum_{k=1}^n\big(y_k - \mathbf{x}_k^T\mathbf{w}_k\big)^2 \\
&= (\mathbf{y} - \mathbf{X} \mathbf{w})^T(\mathbf{y} - \mathbf{X} \mathbf{w})
\end{align}
もう少し式展開してみる。
\begin{align}
\mathbf{E} &= (\mathbf{y} - \mathbf{X} \mathbf{w})^T(\mathbf{y} - \mathbf{Xw}) \\\\
& \cdots \text{単純に展開} \\
&= \mathbf{y}^T \mathbf{y} - (\mathbf{Xw})^T \mathbf{y} -\mathbf{y}^T \mathbf{Xw} + (\mathbf{Xw})^T \mathbf{Xw} \\\\
& \cdots \text{右の転置の変形式を用いる:} (\mathbf{AB})^T = \mathbf{B}^T\mathbf{A}^T, \mathbf{a}^T\mathbf{b} = \mathbf{b}^T \mathbf{a} \\
& = \mathbf{y}^T \mathbf{y} - (\mathbf{w}^T \mathbf{X}^T) \mathbf{y} - \mathbf{w}^T\mathbf{X}^T\mathbf{y} + (\mathbf{w}^T\mathbf{X}^T) \mathbf{Xw} \\
&= \mathbf{y}^T \mathbf{y} - 2\mathbf{w}^T (\mathbf{X}^T \mathbf{y}) + \mathbf{w}^T\mathbf{X}^T \mathbf{Xw} \\
\end{align}
よって、残差2乗和は以下となる。
\therefore \mathbf{E} = \mathbf{y}^T \mathbf{y} - 2\mathbf{w}^T (\mathbf{X}^T \mathbf{y}) + \mathbf{w}^T\mathbf{X}^T \mathbf{Xw}
重回帰:微分して0を解く
微分対象は、各係数$\mathbf{w}$であった。以下の残差2乗和を$\mathbf{w}$で微分し、0になる値を求めればよい。
\mathbf{E} = \mathbf{y}^T \mathbf{y} - 2\mathbf{w}^T (\mathbf{X}^T \mathbf{y}) + \mathbf{w}^T\mathbf{X}^T \mathbf{Xw}
$\mathbf{w}$を持つ項は2つだけ。$2\mathbf{w}^T (\mathbf{X}^T \mathbf{y})$ , $ \mathbf{w}^T\mathbf{X}^T \mathbf{Xw}$
微分1:
■ $2\mathbf{w}^T (\mathbf{X}^T \mathbf{y})$
これをベクトル $\mathbf{w}$ で微分する。
ベクトルでの微分は、ベクトルの各成分の偏微分を計算し、その結果を各成分方向に並べてベクトルを作り、勾配(接する超平面の最も急な傾き方向)を求める操作 内積、$\mathbf{w}^T \cdot \mathbf{x} = w_1 x_1 + w_2 x_2 + \cdots + w_nx_n$ と考えると、\frac{\partial}{\partial\mathbf{w}} \mathbf{w}^T\mathbf{x} = \mathbf{x}
となる。
よって、
\frac{\partial}{\partial\mathbf{w}} 2\mathbf{w}^T (\mathbf{X}^T \mathbf{y}) = 2\mathbf{X^T y}
微分2:2次形式の部
■ $ \mathbf{w}^T\mathbf{X}^T \mathbf{Xw}$
2次形式。ちょっと2次形式の話は長くなる。
$\mathbf{X}^T \mathbf{X} = \mathbf{A}$ とおく → $ \mathbf{w}^T\mathbf{X}^T \mathbf{Xw} = \mathbf{w}^T\mathbf{A}\mathbf{w}$
説明変数$\mathbf{x}$の次元数mとしたとき、$\mathbf{X}^T\mathbf{X}$はm×m次元の正方行列で、$\mathbf{w}$はm次元。
※ただし、$\mathbf{x}$の1次元目は1で固定。前述の通り、$\mathbf{w}$の定数項に対応する最初の次元を1と置くことで$\mathbf{w}^T\mathbf{x}$の内積に対応、および計画行列$\mathbf{X}$に対応させている
$\mathbf{X}^T\mathbf{X} = \mathbf{A}$と書く(正方行列)と、$ \mathbf{w}^T\mathbf{X}^T \mathbf{Xw} = \mathbf{w}^T\mathbf{A}\mathbf{w}$と書ける。
$\mathbf{X}^T\mathbf{X}$ はm×m次元の行列なので、 $\mathbf{A}\mathbf{w}$ の計算結果はm次元のベクトルとなる。
$A$ の要素を横ベクトル$\mathbf{a_i}^T$を用いて以下のように表現できる。
\mathbf{A} = \begin{pmatrix} \mathbf{a_1}^T \\ \mathbf{a_2}^T \\ \vdots \\ \mathbf{a_m}^T \end{pmatrix}
すると、ベクトル内積を2回行う形に解釈でき、以下のように考えられる。
\begin{align}
\mathbf{w}^T\mathbf{A}\mathbf{w} =
\mathbf{w}^T (\mathbf{A}\mathbf{w}) &= \sum_j \sum_i w_j a_{ij} w_i
\end{align}
これの詳細な途中式
\begin{align}
\mathbf{w}^T\mathbf{A}\mathbf{w} = \mathbf{w}^T (\mathbf{A}\mathbf{w})
&= \mathbf{w}^T (\begin{pmatrix} \mathbf{a_1}^T \\ \mathbf{a_2}^T \\ \vdots \\ \mathbf{a_m}^T \end{pmatrix}\cdot \mathbf{w})
= \mathbf{w}^T (\begin{pmatrix} \mathbf{a_1}^T\cdot \mathbf{w} \\ \mathbf{a_2}^T\cdot \mathbf{w} \\ \vdots \\ \mathbf{a_m}^T\cdot \mathbf{w} \end{pmatrix})
\\
&= \mathbf{w}^T(\begin{pmatrix} \sum_i(a_{1i}w_i) \\ \sum_i(a_{2i}w_i) \\ \vdots \\ \sum_i(a_{mi}w_i) \end{pmatrix}) \\
\text{ここで, } \mathbf{s_j} &= \sum_i \mathbf{a}_{ji} w_i \text{とおいて、}\\
\mathbf{w}^T (\mathbf{A}\mathbf{w}) &= \mathbf{w}^T(\begin{pmatrix} \mathbf{s_1} \\ \mathbf{s_2} \\ \vdots \\ \mathbf{s_m} \end{pmatrix})
\\
&= \sum_j\mathbf{w_j}\mathbf{s_j}
\\
\text{ここで, } \mathbf{s_i } &= \begin{pmatrix} \sum_i a_{1i} w_i \\ \sum_ia_{2i} w_i \\ \vdots \\ \sum_i a_{mi} w_i \end{pmatrix}\text{を再度代入すると、}
\\
\mathbf{w}^T (\mathbf{A}\mathbf{w}) &= \sum_j \sum_i w_j a_{ij} w_i
\end{align}
スカラー値、各$a_{ij}w_iw_j$のi, j に対する和なので $m^2$ 個の項の和となっている。
本来スカラー値なので行列のように書くのは正しくないのだが、index i,j を視覚的に分かり易く描くと$\sum_j\sum_iw_ja_{ij}w_i$は以下の図のイメージ。

これを$w_i$に対して微分すると、$w_i$を含む項のみが残り、他の項は削除される。上の図と見比べると、
\begin{align}
\frac{\partial}{\partial w_i} \mathbf{w}^T \mathbf{A} \mathbf{w} &= \frac{\partial}{\partial w_i} \sum_j \sum_i w_j a_{ij} w_i \\
&= a_{1i}w_1 + a_{2i}w_2 + a_{3i}w_3 + \cdots + a_{mi} w_m + \\
& \quad w_1a_{i1} + w_2a_{i2} + w_3a_{i3} + \cdots + w_ma_{im}
\end{align}
結局これもベクトルの内積の和に見える。
\frac{\partial}{\partial w_i} \mathbf{w}^T \mathbf{A} \mathbf{w} = \mathbf{a_i}\mathbf{w} + \mathbf{a_i}^T\mathbf{w}
行列$\mathbf{A}$は、$\mathbf{X}^T\mathbf{X}$ なので対称行列。
よって、行列$\mathbf{A}$の行ベクトル部を $\mathbf{a_i}^T$ とした。
これをベクトル $\mathbf{w}$ で微分する。
ベクトルでの微分は、ベクトルの各成分の偏微分を計算し、その結果を各成分方向に並べてベクトルを作り、勾配(接する超平面の最も急な傾き方向)を求める操作
\begin{align}
\frac{\partial}{\partial \mathbf{w}}\mathbf{w}^T\mathbf{A}\mathbf{w} &=
\begin{pmatrix}
\frac{\partial}{\partial\mathbf{w_1}}\mathbf{w}^T\mathbf{A}\mathbf{w} \\
\frac{\partial}{\partial\mathbf{w_2}}\mathbf{w}^T\mathbf{A}\mathbf{w} \\
\frac{\partial}{\partial\mathbf{w_3}}\mathbf{w}^T\mathbf{A}\mathbf{w} \\
\vdots \\
\frac{\partial}{\partial\mathbf{w_m}}\mathbf{w}^T\mathbf{A}\mathbf{w} \\
\end{pmatrix}
\\
&=
\begin{pmatrix}
\mathbf{a_1}\mathbf{w} + \mathbf{a_1}^T\mathbf{w} \\
\mathbf{a_2}\mathbf{w} + \mathbf{a_2}^T\mathbf{w} \\
\mathbf{a_3}\mathbf{w} + \mathbf{a_3}^T\mathbf{w} \\
\vdots \\
\mathbf{a_m}\mathbf{w} + \mathbf{a_m}^T\mathbf{w} \\
\end{pmatrix}
\\
&= \mathbf{A}\mathbf{w}+\mathbf{A}^T\mathbf{w} \\
&= ( \mathbf{A} + \mathbf{A}^T ) \mathbf{w}
\end{align}
こんなに頑張ったのに、結果たったこれだけの式に帰着する。
以上が、微分のうち、2次形式$\mathbf{w}^T\mathbf{X}^T\mathbf{X}\mathbf{w}$を微分すると?の件。
微分全体に話を戻す
■誤差の微分の話に戻る
残差2乗和は以下であった
\mathbf{E} = \mathbf{y}^T \mathbf{y} - 2\mathbf{w}^T (\mathbf{X}^T \mathbf{y}) + \mathbf{w}^T\mathbf{X}^T \mathbf{Xw}
第2項目は
$\frac{\partial}{\partial\mathbf{w}}2\mathbf{w}^T(\mathbf{X^T y}) = 2\mathbf{X^T y}$
第3項目(2次形式部)は
$\frac{\partial}{\partial\mathbf{w}}\mathbf{w}^T\mathbf{X}^T \mathbf{Xw}= (\mathbf{X^T X} + (\mathbf{X^T X})^T)\mathbf{w} = 2\mathbf{X}^T\mathbf{X}\mathbf{w}$
よって、重回帰の解である、残差2乗和の微分=0の式は、
\begin{align}
\frac{\partial E}{\partial\mathbf{w}} &= \frac{\partial}{\partial\mathbf{w}} (\mathbf{y}^T \mathbf{y} - 2\mathbf{w}^T (\mathbf{X}^T \mathbf{y}) + \mathbf{w}^T\mathbf{X}^T \mathbf{Xw}) \\
& = - 2\mathbf{X^T y} + 2\mathbf{X}^T\mathbf{X}\mathbf{w} \\
&= 0 \\
\Rightarrow \mathbf{X}^T\mathbf{X}\mathbf{w} &= \mathbf{X^T y} \\
\mathbf{w} &= (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X^T y}
\end{align}
結局、重回帰を解く式は、
\mathbf{w} = (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X^T y}
驚くほど簡単な式になる。
これを重回帰の正規方程式と呼ぶ。
まとめ:モデル式
\mathbf{\hat{y}}^T = \mathbf{X} \mathbf{w}
最小二乗法、残差二乗和
\mathbf{E} = \mathbf{y}^T \mathbf{y} - 2\mathbf{w}^T (\mathbf{X}^T \mathbf{y}) + \mathbf{w}^T\mathbf{X}^T \mathbf{Xw}
残差二乗和のw微分=0
\begin{align}
\frac{\partial E}{\partial\mathbf{w}} &= \frac{\partial}{\partial\mathbf{w}} (\mathbf{y}^T \mathbf{y} - 2\mathbf{w}^T (\mathbf{X}^T \mathbf{y}) + \mathbf{w}^T\mathbf{X}^T \mathbf{Xw}) \\
& = - 2\mathbf{X^T y} + 2\mathbf{X}^T\mathbf{X}\mathbf{w} \\
&= 0 \\
\Rightarrow \mathbf{X}^T\mathbf{X}\mathbf{w} &= \mathbf{X^T y} \\
\mathbf{w} &= (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X^T y}
\end{align}
結局、重回帰を解く式は、
\mathbf{w} = (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X^T y}
