【GPT-4o, Gemini 1.5 Flash】LLMたちに競プロの問題解かせてみた【結果編】

はじめに

OpenAIはgpt2としてテストされていたものをGPT-4oとして公開しましたね。この伏線回収には少し驚きました。また、googleもGemini 1.5 Proの新機能、Gemini 1.5 Flashの発表などここ数日LLM界隈？はかなり盛り上がってそうです。
ここで、一つの疑問が生まれました。「これだけLLMが進化したなら青色くらいの実力があるのでは・・・？」この疑問を解決するため、気になったモデルたちで競プロの問題がどれだけ解けるか競いたいと思います。

ルール

解答方法

• 対象コンテストの各問題をAから順に解いていく
• すべてのLLMで同一のプロンプトを使用する
• 各問題に対して、解答を3回挑戦させる

正誤失格判定

• 3回中1回でも正答できれば、問題を正答したとする
• 3回すべて間違えれば、誤答
• 2問誤答した時点で失格となる

順位付け

• 各コンテストについて問題の難しさ（Difficulty）の総和をスコアとして、その大きさで順位付けを行う
  • 同率の場合、各コンテストの正答数が多いLLMを上位とする
  • なお同率の場合、上位の順位に合わせる
• それぞれの順位の勝点は1位が3点、2位が2点、3位が1点
• 各コンテストの勝点を合算し、一番高い勝ち点のLLMが優勝

Difficultyの参考

今回比較するLLMたち

以下の５つについて、APIを使用して検証していきます。ただし、ClaudeはAPIの個人利用が推奨されていないのでWebブラウザ上で実行しました。

• GPT-4o：gpt-4o-2024-05-13
• GPT-4 Turbo：gpt-4-turbo-2024-04-09
• Gemini 1.5 Pro：gemini-1.5-pro-latest
• Gemini 1.5 Flash：gemini-1.5-flash-latest
• Claude 3 Opus：claude-3-opus-20240229

対象コンテスト

以下の３つのコンテストで競い合います。

ABC344

ABC346

ABC352

入力されるプロンプト

問題を画像のようにを入力例を一つ含むようにSnipping Toolでスクショします。赤く囲った部分を押すことで文字を画像から読み取ってくれます。

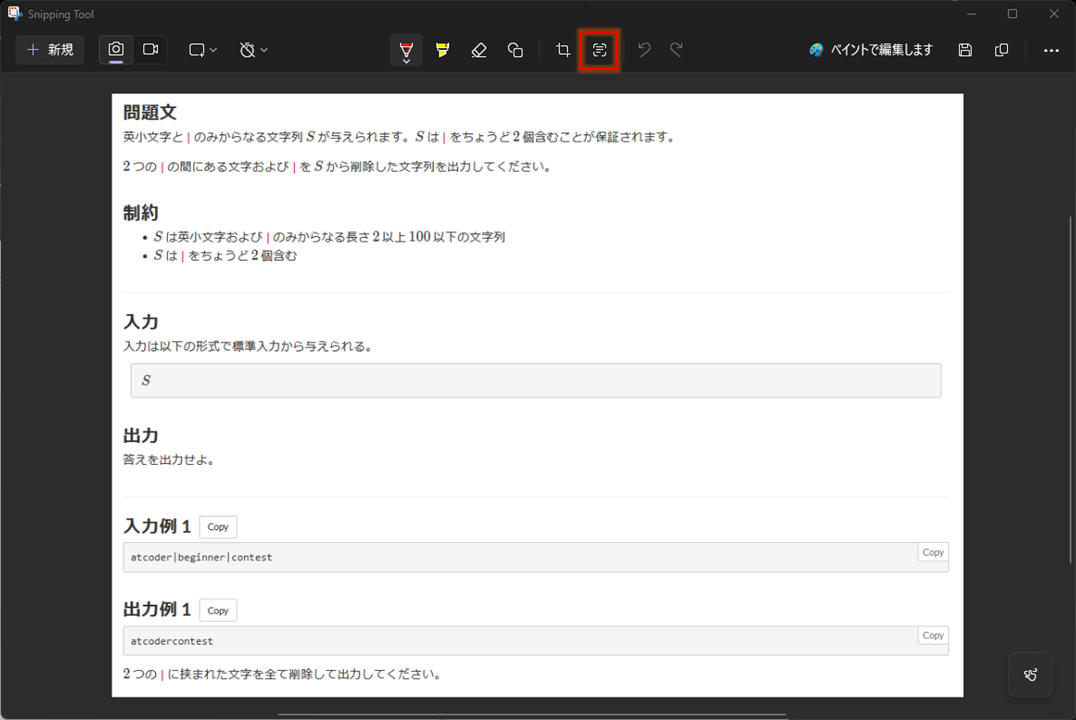
読み取ったままではごみが多いので、整形し下記のようなプロンプトになります。

ABC344 問題Aのプロンプト

abc344a_prompt.txt

### 指示
問題文に従ってコードを生成してください。
### 条件
コードのみ出力してください
実行時間制限は2秒以内です
メモリ制限は1024MB以内です
計算量は10^7程度を目安にしてください
### 問題文
英小文字と|のみからなる文字列Sが与えられます。Sは|をちょうど2個含むことが保証されます。

2つの|の間にある文字および|をSから削除した文字列を出力してください。

制約
·Sは英小文字および|のみからなる長さ2以上100以下の文字列
·Sは|をちょうど2個含む

入力
入力は以下の形式で標準入力から与えられる。
S

出力
答えを出力せよ。

入力例1
atcoder|beginner|contest

出力例1
atcodercontest

2つの|に挟まれた文字を全て削除して出力してください。

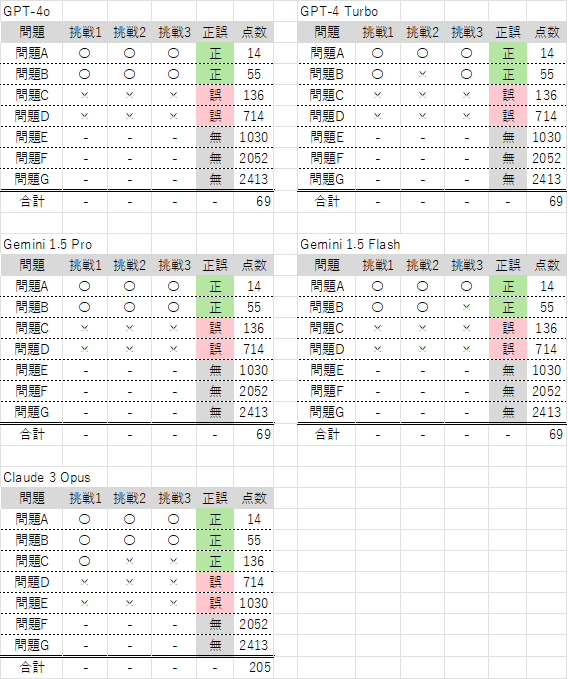
結果

ここでは結果のみを載せます。詳細や感想については各コンテストのリンクに飛んでください。

全入出力リンク

各コンテスト詳細

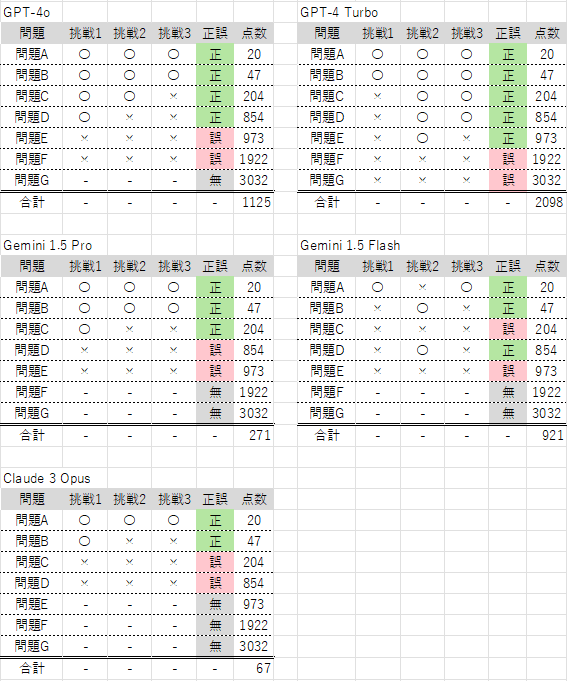
ABC344

全結果

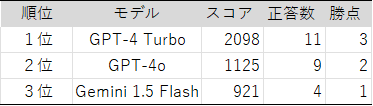
順位

ABC346

全結果

順位

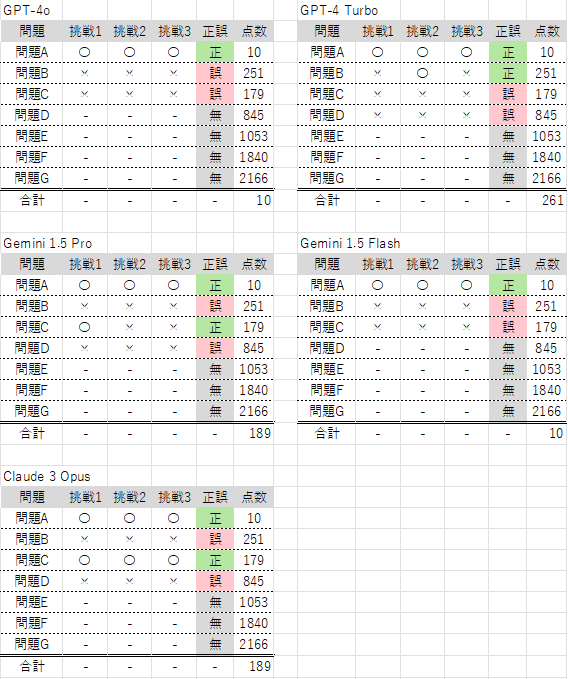
ABC352

全結果

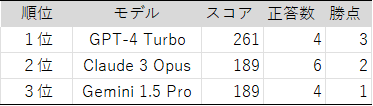
順位

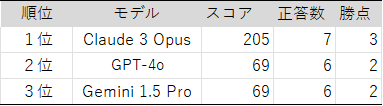
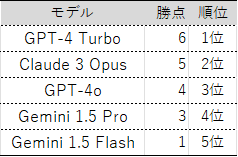
総合順位

総評

GPT-4 TurboとGPT-4o

今回の検証ではGPT-4 Turboが一番強いという結果になりました。GPT-4oについて、多くの人がその性能について騒いでいましたが、競プロを解くという文脈で難しい問題が解けるようになったかというとそうではなかったようです。ただ、返答速度は格段に上がっていましたし、音声処理や画像処理面も強化されていて、マルチモーダルAIとしてのレベルは上がっていることを感じました。

GeminiとClaude

ABC346の問題CではGPT-4系列が誤答しているのに対し、Gemini 1.5 ProとClaude 3 Opusについては正答しています。（Claude 3 Opusに関しては全解答AC）GPTにできない問題があって、GeminiやClaudeでできる問題があることを知れたのはというのは大きな収穫でした。
また、Gemini 1.5 FlashはABC344の問題Dが解けています。他の結果を見る限り、たまたま良い結果が出たのだと思いますが、LLMの出力が確率事象であることを改めて感じさせてくれました。

全体の評価

ABC344はともかく、ABC346、ABC352の結果からLLMを過小評価してしまいそうになりますが、実はそうではないと思います。例えば、下記のようにDifficultyが1000を超える問題でも使うアルゴリズムなど方針自体はあっていることが多かったです。このように、問題を解く上で方針を正しく立てるという目的で使われてしまえば、解答までの時間が減りより多くの問題が解けるようになると思います。
さらに、得意な問題が違うなら両方のLLMで出力し比較させればよいし(LLM Chain)、プロンプトエンジニアリングやRAGなど制御するような技術を本格的に使えば、より高いDifficultyの問題を解けるようになってしまうと思いました。

方針がうまく立てられているコード

abc352e_claude3opus_3.cpp

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

const int MAX_N = 200005;

int N, M;
vector<pair<int, pair<int, int>>> edges;
int parent[MAX_N];

int find(int x) {
    if (parent[x] == x) return x;
    return parent[x] = find(parent[x]);
}

void unionSet(int x, int y) {
    int rootX = find(x);
    int rootY = find(y);
    if (rootX != rootY) {
        parent[rootX] = rootY;
    }
}

int main() {
    cin >> N >> M;

    for (int i = 1; i <= N; i++) {
        parent[i] = i;
    }

    for (int i = 0; i < M; i++) {
        int K, C;
        cin >> K >> C;

        vector<int> vertices(K);
        for (int j = 0; j < K; j++) {
            cin >> vertices[j];
        }

        for (int j = 0; j < K - 1; j++) {
            for (int k = j + 1; k < K; k++) {
                int u = vertices[j];
                int v = vertices[k];
                edges.push_back({C, {u, v}});
            }
        }
    }

    sort(edges.begin(), edges.end());

    long long total_weight = 0;
    int connected_components = N;

    for (auto edge : edges) {
        int weight = edge.first;
        int u = edge.second.first;
        int v = edge.second.second;

        if (find(u) != find(v)) {
            unionSet(u, v);
            total_weight += weight;
            connected_components--;
        }
    }

    if (connected_components == 1) {
        cout << total_weight << endl;
    } else {
        cout << -1 << endl;
    }

    return 0;
}