LLMに競プロの問題解かせてみた【ABC352】

はじめに

ルールやスコアの計算方法などは結果編に記載しています。

結果編

問題解説（C~E）

一応私も解いて解説しているのでリンクしておきます

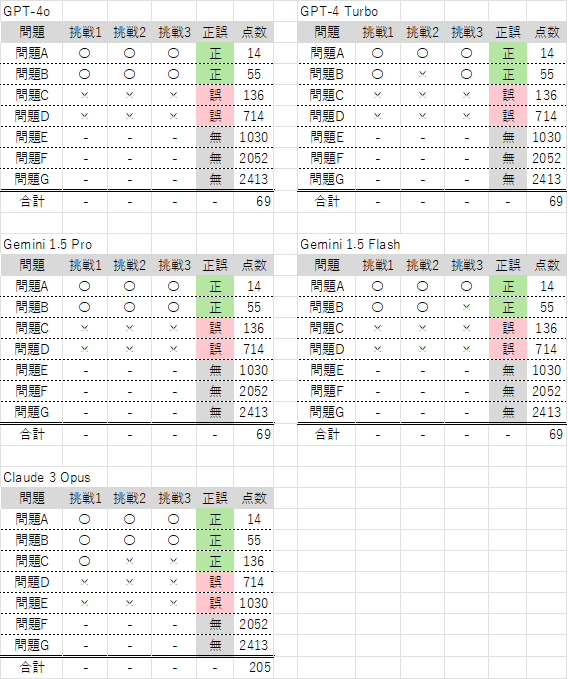
結果

下記コンテストの問題をルールに基づいて解かせた結果です。

各問題の所感

問題A

Difficulty: 14

下記のように二通りの解き方がありました。

Gemini 1.5 Pro：挑戦1の出力

abc352a_geminipro_1.py

N, X, Y, Z = map(int, input().split())

if X < Y:
  if X < Z < Y:
    print("Yes")
  else:
    print("No")
else:
  if Y < Z < X:
    print("Yes")
  else:
    print("No")

Gemini 1.5 Flash：挑戦1の出力

abc352a_geminiflash_1.py

n, x, y, z = map(int, input().split())

if x < y:
  if z in range(x, y + 1):
    print("Yes")
  else:
    print("No")
else:
  if z in range(y, x + 1):
    print("Yes")
  else:
    print("No")

問題B

Difficulty: 55

GPT-4 Turboのミスはmainを実行し忘れていて、Gemini 1.5 Flashは考え方が間違っていました。GPT-4 Turboのmainの中身はあっていたので惜しいという感じです。

abc352b_gpt4turbo_2.py

def main():
    import sys
    input = sys.stdin.read
    data = input().split()
    S = data[0]
    T = data[1]
    
    s_len = len(S)
    t_len = len(T)
    
    result = []
    t_idx = 0
    s_idx = 0
    
    # Traverse String T comparing it to S
    while s_idx < s_len and t_idx < t_len:
        if S[s_idx] == T[t_idx]:
            result.append(t_idx + 1)  # +1 because indices in the output need to be 1-based
            s_idx += 1
        t_idx += 1
    
    # Output all indices
    print(" ".join(map(str, result)))

問題C

Difficulty: 136

でかい頭を一番上にする問題です。LLMならば、$B_i - A_i$が頭の大きさということに気が付けば解けると思います。数々のLLMが間違える中、Claude 3 Opusはやってくれました！

ABC346CといいClaude 3 OpusはほかのLLMが躓くような数学的な問題はある程度できるのか？（ただし、ABC344Cは間違えている。数学的には間違えていないがsetを使うことができなかった）

abc352c_claude3opus_1.cpp

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

int main() {
    int N;
    cin >> N;

    vector<pair<int, int>> giants(N);
    for (int i = 0; i < N; i++) {
        cin >> giants[i].first >> giants[i].second;
    }

    sort(giants.begin(), giants.end(), [](const pair<int, int>& a, const pair<int, int>& b) {
        return a.second - a.first < b.second - b.first;
    });

    long long maxHeight = 0;
    for (const auto& giant : giants) {
        maxHeight += giant.first;
    }
    maxHeight += giants.back().second - giants.back().first;

    cout << maxHeight << endl;

    return 0;
}

問題D

Difficulty: 714

この問題はどのLLMも解けてません。一番びっくりしたのは途中でコメントが中国語になってたのです。この回答からは近い回答方針のものを選んで貼り付けてるだけという印象を受けました。少し応用されると対応できないのだろうか？

abc352d_gpt4turbo_3.py

def main():
    import sys
    import collections
    input = sys.stdin.read
    data = input().split()
    N = int(data[0])
    K = int(data[1])
    P = list(map(int, data[2:]))

    if K == 1:
        # K==1の場合、どの単独の要素も連続する整数列{Pi}から選ばれていると見なす。
        print(0)
        return

    # 各要素が集合{a, a+1, ..., a+K-1}のどれに対応するか記録
    pos_mod = collections.defaultdict(list)
    for i in range(N):
        pos_mod[P[i] % K].append(i)

    # 全てのmod k に対して、ぴったりK個連続する整数が選べるK個づつの範囲をみつける
    min_diff = float('inf')
    
    for key, indices in pos_mod.items():
        # indices には、同じ mod K の要素のインデックスが入っている。
        if len(indices) >= K:
            # ソートされたindexが必要
            indices.sort()
            # スライドする幅Kのウインドウで見ていく
            for i in range(len(indices) - K + 1):
                # 最初の添字と最末尾の添字
                start = indices[i]
                end = indices[i + K - 1]
                # 这里我们注意到需要的是位置差距，所以要检查内容上的连续性
                value_range = P[start:end+1]
                value_range.sort()
                if all(value_range[j] == value_range[0] + j for j in range(K)):
                    # 更新最小差值
                    min_diff = min(min_diff, end - start)

    print(min_diff)

main()

問題E

Difficulty: 1030

Claude 3 Opusのみ生き残っています。ぱっとみあってるように見えました。UnionFindを使うことはわかっていて、最小全域木の解法も知ってそうでした。

abc352e_claude3opus_3.cpp

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

const int MAX_N = 200005;

int N, M;
vector<pair<int, pair<int, int>>> edges;
int parent[MAX_N];

int find(int x) {
    if (parent[x] == x) return x;
    return parent[x] = find(parent[x]);
}

void unionSet(int x, int y) {
    int rootX = find(x);
    int rootY = find(y);
    if (rootX != rootY) {
        parent[rootX] = rootY;
    }
}

int main() {
    cin >> N >> M;

    for (int i = 1; i <= N; i++) {
        parent[i] = i;
    }

    for (int i = 0; i < M; i++) {
        int K, C;
        cin >> K >> C;

        vector<int> vertices(K);
        for (int j = 0; j < K; j++) {
            cin >> vertices[j];
        }

        for (int j = 0; j < K - 1; j++) {
            for (int k = j + 1; k < K; k++) {
                int u = vertices[j];
                int v = vertices[k];
                edges.push_back({C, {u, v}});
            }
        }
    }

    sort(edges.begin(), edges.end());

    long long total_weight = 0;
    int connected_components = N;

    for (auto edge : edges) {
        int weight = edge.first;
        int u = edge.second.first;
        int v = edge.second.second;

        if (find(u) != find(v)) {
            unionSet(u, v);
            total_weight += weight;
            connected_components--;
        }
    }

    if (connected_components == 1) {
        cout << total_weight << endl;
    } else {
        cout << -1 << endl;
    }

    return 0;
}

まとめ

• LLMで方針を立てるという使い方はできそう
• 使用するアルゴリズムはわかるが、少し応用されると中身がうまく書けていない
• Claude 3 Opusは数学的な問題が比較的得意かもしれない