最近RNNやSLTMについて勉強するにあたって、自分の研究室にあった『詳解 ディープラーニング(第1版)』(巣籠悠輔著)という本を参考にしてKerasでモデルを作ってみたので、その内容をまとめます。
今回実装したコードはここ(google colab)にまとめてあります。ただ、3.3節以前と第6章の一部は実装していません。また、「Kerasによる実装」と題された部分のみの実装となります。
実行環境
今回の実装にはGoogle Colaboratoryを使用しました。
一応、実装時点での使用したライブラリ等のバージョンを書いておきます。
print(sys.version)
# 3.10.12 (main, Nov 20 2023, 15:14:05) [GCC 11.4.0]
print(np.__version__)
# 1.23.5
print(tf.__version__)
# 2.14.0
print(keras.__version__)
# 2.14.0
print(sklearn.__version__)
# 1.2.2
ライブラリのインポート
今回の実装で使用するライブラリ等をインポートします。
import numpy as np
import tensorflow as tf
from keras.models import Sequential
from keras.layers import Dense, Avtivation
from keras.optimizers import SGD
3.4節「ロジスティック回帰」
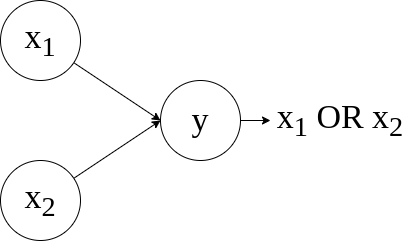
2つの入力をとるORゲートの出力を学習する1層のモデルを実装します。
下図のような、ごく単純なモデルです。
ここでは、活性化関数にシグモイド関数を用いて確率勾配効果法で学習を行います。
モデルの定義
Kerasでモデルを実装するには、まずSequentialメソッドでモデルを定義します。
model = Sequential()
次に、定義したモデルにadd()を使って層を追加していきます。
model.add(Dense(2, units=1))
model.add(Activation('sigmoid'))
Denseは全結合層を意味します。第一引数には入力の次元を渡し、unitsで出力の次元を指定します。
Activationでは活性化関数を指定します。ここではシグモイド関数が指定されています。
また、以下のように書いても同じモデルを定義できます。
model = Sequential([
Dense(2, units=1),
Activation('sigmoid')
])
訓練プロセスの設定
続いて、訓練プロセスを設定します。
いくつか設定可能な項目がありますが、ここでは
- 損失関数は2値クロスエントロピー誤差関数を用いる。
- 最適化手法には確率勾配効果法を用いる。
の2点を設定します。
モデルの訓練プロセスを設定するには、以下のようにcompileメソッドを使用します。
model.compile(loss='binary_crossentropy', optimizer=SGD(learning_rate=0.1))
lossでは損失関数を、optimaizerでは最適化手法を指定します。
SGDに渡しているlerning_rateは学習率を表しています。
データの用意と学習の実行
ORゲートにおける各入力と出力との対応(正解データ)を用意します。
X = np.array([[0, 0], [0, 1], [1, 0], [1,1]])
Y = np.array([[0], [1], [1], [1]])
そして、このデータを用いて学習を行います。
モデルの学習はfit()メソッドを呼び出すだけで実行できます。
model.fit(X, Y, epochs=200, batch_size=1)
epochsはエポック数、batch_sizeはミニバッチの大きさをそれぞれ表しています。
このコードを実行すると、以下のように各エポックでの学習状況が表示されます。
output
Epoch 1/200
4/4 [==============================] - 1s 6ms/step - loss: 1.4456
Epoch 2/200
4/4 [==============================] - 0s 4ms/step - loss: 1.2382
// ...
Epoch 200/200
4/4 [==============================] - 0s 3ms/step - loss: 0.1201
学習結果の確認
以下の2行を呼び出せば、今回の学習の結果を取得できます。
classes = (model.predict(X) > 0.5)
prob = model.predict(X,batch_size=1)
classesにはニューロンが発火するかしないか(つまり、分類されたパターン)が、probには出力の確率が入ります。
出力させると以下のようになります。
print("分類パターン\n" + str(classes))
print("\n確率\n" + str(prob))
分類パターン
[[False]
[ True]
[ True]
[ True]]
確率
[[0.22707717]
[0.91292393]
[0.91291994]
[0.9973342 ]]
上から順に、[0,0], [0,1], [1,0], [1,1]が入力されたときの結果になっています。
これで一応、ORゲートの学習ができました。
おわりに
今回は、Kerasを使用したモデルの構築を試してみました。
colabでは書籍に書いてある他のモデルも構築したので、こちらについてもいつか記事にしたいと思っています。
初投稿で至らない箇所もあったかと思いますが、最後までお付き合い下さりありがとうございました。
参考
今回参考にした書籍の著者の方が以下のgithubでコードを公開されているので、実装される場合はそれも参考にされると良いと思います。
ただ、どちらのコードも少し古く、現在のcolabの環境では動作しないことがありましたので、適宜修正してください(私の実装したコードの動作確認はしてあります)。
また、nkmkさんがkerasの使い方をまとめて下さっているので、こちらも参考になると思います。