LoginSignup
17
16

More than 1 year has passed since last update.

@StoneRIeverKS(S R)

傾向スコアを使った因果効果の推定方法

Posted at

はじめに

　調査観察データの統計科学に記載の傾向スコアを使った因果効果の推定手法とpythonコードをまとめました。本記事では最初に傾向スコアの定義をして、次に共変量調整の方法を記載します。共変量調整の方法としては、傾向スコアマッチング、層別解析、IPW、カーネルマッチングを記載しました。最後にこれらの手法をpythonで実装し、シミュレーションを実施した結果を記載します。

\def\middlemid{\;\middle|\;}
\def\set#1{\left\{{#1}\right\}}
\def\setin#1#2{\left\{{#1} \middlemid {#2}\right\}}
\def\sub#1#2{{#1}_{#2}}

傾向スコア

　傾向スコアの定義は下記のようになります。第$i$被験者の介入変数を

Z_i = \left\{
\begin{array}{ll}
1 & (介入があった場合) \\
0 & (介入がなかった場合)
\end{array}
\right.

とします。また、第$i$被験者の共変量を$\boldsymbol{x}_i$とします。このとき、第$i$被験者の傾向スコアは
$$e_i = P(Z_i=1|\boldsymbol{x}_i)$$
と定義されます。

　傾向スコアを使って共変量を調整することで、セレクションバイアスを排除した介入の効果を推定することが今回の目的です。傾向スコアを使ってセレクションバイアスを排除する必要性については、効果検証入門にめちゃくちゃわかりやすく書かれています。

共変量調整の方法(理論)

傾向スコアマッチング

　最も一般的(?)な方法。介入群と対照群で傾向スコアが同じ被験者をペアにしてその結果変数の差を取り、その差の平均を因果効果の推定値とする手法です。数式で表すと下記のようになります。

\tau = E_e[E[Y_1|e, Z=1]-E[Y_0|e, Z=0]].　\tag{1}

ただし、$Y_1, Y_0$はそれぞれ介入があった場合の結果変数と、介入がなかった場合の結果変数です。また、$\tau$は推定対象の因果効果で$\tau = E[Y_1-Y_0]$です。1この数式をつぶさに見てみると、最初に$E[Y_1|e, Z=1]-E[Y_0|e, Z=0]$を計算し、それを傾向スコア$e$について平均を取っています。感覚的には$E[Y_1|e, Z=1]-E[Y_0|e, Z=0]$の計算が「介入群と対照群で傾向スコアが同じ被験者をペアにしてその結果変数の差を取り」に対応し、$e$による平均の計算が、「その差の平均」の計算に対応しています。
　傾向スコアマッチングは直感的で非常にわかりやすい一方で、傾向スコアが完全に同じ介入群と対照群の被験者をペアにできるのかという問題をはらんでいます。実際、傾向スコアは0から1の間の実数なので、傾向スコアが完全に同じペアは存在しない場合が多いです。そこで、傾向スコアが最も近い被験者同士をマッチングさせる最近傍マッチングや、介入群の各被験者の傾向スコアに最も近い$M$人の対照群の被験者をマッチングさせる1対多のマッチングなどが提案されています。後で記載するpythonのコードには最も基本的な最近傍マッチングを実装しています。

層別解析

　傾向スコアマッチングでは、完全に同じ傾向スコアでマッチングさせることは不可能であることが多いと書きました。そこで、マッチングさせるのではなく傾向スコアの値によって層を複数作り、各層で因果効果を推定し、それらの平均をとることで因果効果を推定するという方法が提案されました。この手法を層別解析と呼びます。
　具体的に数式で表すと因果効果の推定量は、下記となります。

\hat{\tau} = \sum_{k=1}^K \frac{N_k}{N} (\bar{y_1}_k-\bar{y_0}_k) \tag{2}

ただし、被験者全体のサンプルサイズを$N$、第$k$層のサンプルサイズを$N_k$、第$k$層の介入群の結果変数の平均を$\bar{y_1}_{k}$、対照群の結果変数の平均を$\bar{y_0}_k$としています。
　層の数については分析者が決めるパラメータであり、調査観察データの統計科学によれば、5層が使われることが多いそうです。(理論的な根拠はないそうですが...。

IPW推定量

　傾向スコアマッチングと層別解析の基本的な考え方は、介入群と対照群の被験者をペアにすることで因果効果を推定します。しかし、これらの方法はマッチングの仕方や層数の決め方が分析者任せであり、恣意的であるとの批判がありました。そこで、傾向スコアを使って結果変数を重みづけることで因果効果の推定量を導く方法としてIPW推定量が提案されています。
　IPW推定量とは、

\hat{\mu_1} = \sum_{i}^N \frac{Z_i Y_i}{e_i}/\sum_{i=1}^N\frac{Z_i}{e_i}, \ \ \hat{\mu_0} = \sum_{i=1}^N \frac{(1-Z_i) Y_i}{1-e_i}/\sum_{i=1}^N \frac{1-Z_i}{1-e_i} \tag{3}

です。ただし、$\hat{\mu_1},\hat{\mu_0}$は $\mu_1 = E[Y_1], \mu_0 = E[Y_0]$の推定量です。2
　IPW推定量の良さの一つは、漸近正規性を持つことです。すなわち、
$$\sqrt{N}(\hat{\mu_1}-\hat{\mu_0}-\mu_1-\mu_0) \stackrel{d}{\longrightarrow } N(0, V(\theta_0))$$
が成り立ちます。3　したがって、被験者数が十分に大きいときは、IPW推定量を使うことを検討すると良いと考えています。(実装も簡単！)

カーネルマッチング

　傾向スコアマッチングの課題は、傾向スコアが同じ被験者が介入群と対照群に存在しないことでした。それに対してカーネルマッチングの基本的な考え方は傾向スコアが同じ被験者が介入群と対照群に存在しないなら作ってしまえです。
　ということで、傾向スコアから結果変数を予測するモデルを作成し、介入群の介入を受けていない場合の結果変数を傾向スコアから予測し、観測されている介入があったときの結果変数から、予測された結果変数を引くことで因果効果を推定する手法が提案されています。文章で書くと意味不明なので、手順を追って説明します。

  1. 対照群の傾向スコア$e_0$から結果変数$Y_0$を予測するモデルを作成する。これを$Y_0 = f(e_0)$とする。
  2. 介入群の各被験者の傾向スコア$e_{1i}$から、介入を受けていない場合の結果変数を1のモデルで予測する。これを$\hat{Y}_{0i} = f(\sub{e}{1i})$とする。
  3. 観測されている介入群の結果変数から、2で予測した介入群の介入を受けていない場合の結果変数を引く。これを$\sub{Y}{1i}-\sub{\hat{Y}}{0i}$とする。
  4. 3で求めた差分の平均を取り、因果効果を推定する。すなわち、$\hat{\tau} = \frac{1}{\sub{N}{1}}\sum_{i=1}^{N_1}(\sub{Y}{1i}-\sub{\hat{Y}}{0i})$とする。($N_1$は介入群のサンプルサイズ)

この方法で大事なのは、モデル$f$の精度です。傾向スコアから結果変数を予測するモデルは無数に存在しますが、ここでは局所回帰モデルすなわち、カーネルで重みづけられた回帰モデルを使います。そのため、カーネルマッチングという名前がついています。局所回帰モデルについては、局所線形回帰を完全に理解したいが超絶分かりやすかったです。また、調査観察データの統計科学の付録でも局所回帰の雰囲気は理解できます。

手法の比較

　ここまで、傾向スコアマッチング・層別解析・IPW推定量・カーネルマッチングについて述べてきました。手法がいくつか出てくると、それらを比較してより良い手法を選択したくなりますよね。効果検証入門によれば、平均のつり合いを見ることである程度手法の精度を評価することができます。
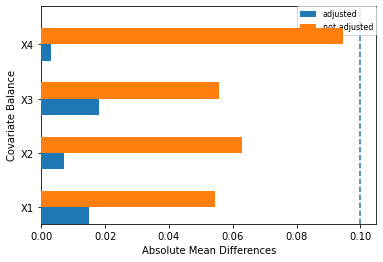
　具体的には、各手法ごとに下図を作成して比較します。
AMD.png
上図の縦軸は共変量、オレンジ色、青色の棒グラフはそれぞれ調整前と調整後の介入群と対照群の共変量の差の絶対値を表しています。これらは各手法によって算出の仕方が異なりますが、基本的には介入群と対照群の共変量の平均を出すという考え方で問題ないです。介入群の第$i$被験者の共変量を$X_{m1i}$、対照群の第$j$被験者の共変量を$X_{m0j}$とします。($m$は上図では1,2,3,4のいずれか)

  • 調整前の共変量の差の絶対値
    1. 介入群と対照群の各共変量の平均を算出する。つまり、$\sub{\bar{X}}{m1} = \frac{1}{N_1}\sum_{i=1}^{N_1}X_{m1i}$と$\sub{\bar{X}}{m0} = \frac{1}{N_0}\sum_{j=1}^{N_0}X_{m0j}$を計算する。
    2. 共変量の平均の差の絶対値を計算する。つまり、$|\sub{\bar{X}}{m1}-\sub{\bar{X}}{m0}|$を計算する。これが、オレンジ色の棒グラフである。
  • 調整後の共変量の差の絶対値
    • 傾向スコアマッチングの場合
      1. 介入群の第$i$被験者と対照群の第$j$被験者がマッチングされたとする。このとき、それぞれの共変量の差分を計算する。つまり、$X_{m1i}-X_{m0j}$を計算する。
      2. 共変量の差分の平均をとり、絶対値を計算する。つまり、$|\frac{1}{N_1} \sum(X_{m1i}-X_{m0j})|$を計算する。これが、傾向スコアマッチングの場合の青色の棒グラフである。
    • 層別解析の場合
      1. (2)式の$\bar{y_1}_k, \bar{y_0}_k$をそれぞれ$\sub{\bar{X}}{m1}, \sub{\bar{X}}{m0}$に入れ替える。
      2. 入れ替えた後の式に絶対値をつけた値を計算する。これが層別解析の場合の青色の棒グラフである。
    • IPW推定量の場合
      1. (3)式の$Y_i$をそれぞれ$X_{mi}$に置き換える。
      2. 置き換えた$\hat{\mu}_0, \hat{\mu}_1$の差分の絶対値を計算する。これがIPW推定量の場合の青色の棒グラフである。

カーネルマッチングについては、上記のような評価をすることができません。したがって、傾向スコアマッチングとカーネルマッチング間で比較をすることは難しいです。しかし、カーネルマッチングで用いられるモデル間での評価をすることはできます。カーネルマッチングにおいては、重みづけに使うカーネル、カーネルのバンド幅、回帰の次元数などがハイパーパラメータとなりますが、これらを変えて汎化性能が良いモデルを選択することで、ある程度の精度は担保できると考えられます。

シミュレーション

シミュレーションデータ

下記の条件でシミュレーションデータを生成しました。

  • サンプルサイズ：$N=10^3$
  • 共変量の次元数：$M = 4$
  • 共変量の分布：全て$[-1, 0]$の一様分布
  • 真の傾向スコアのモデル：$P(Z=1|X_1, X_2, X_3, X_4) = \frac{1}{1+{\rm exp}(-X_1-X_2-X_3-X_4)}$
  • 真の結果変数と共変量・介入の関係：$Y = X_1+2X_2+3X_3+4X_4+Z$

この条件に合わせてシミュレーションデータを発生させます。

シミュレーションデータの発生
#import
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

#シミュレーション用のパラメータの設定
##サンプルサイズ
N = 10**3

##共変量の次元数
K = 4
cov_list_str = ["X1", "X2", "X3", "X4"]

##一様分布の範囲
a, b = [-1, 0]

#汎用関数
##真の傾向スコアのモデル
def propensity_score(vec, coef = np.array([-1, -1, -1, -1])):
    linear = vec*coef
    return(1/(1+np.exp(np.sum(linear))))

##真の結果変数
def result(vec, coef = np.array([1, 2, 3, 4, 1])):
    linear = vec*coef
    return(np.sum(linear))

#シミュレーションデータの生成
##共変量作成
df = pd.DataFrame((b-a)*np.random.rand(N,K)+a, columns = cov_list_str)

##真の傾向スコアの計算
true_propensity_score = pd.DataFrame(df.apply(propensity_score, axis=1), columns = ["true_propensity_score"])

##真の傾向スコアをもとのデータフレームにマージ
df_true_ps = pd.merge(df, true_propensity_score, how="left", left_index=True, right_index=True)

##真の傾向スコアに基づき介入変数を乱数で発生させる
treatment = pd.DataFrame([np.random.binomial(n=1, p=p) for p in true_propensity_score["true_propensity_score"]], columns = ["treatment_flg"])

##介入変数をもとのデータフレームにマージ
df_treatment = pd.merge(df_true_ps, treatment, how="left", left_index=True, right_index=True)

##結果変数を計算
Y = df_treatment[cov_list_str+["treatment_flg"]].apply(result, axis=1)
result = pd.DataFrame(Y, columns = ["result"])

##結果変数をもとのデータフレームにマージ
df_result = pd.merge(df_treatment, result, how="left", left_index=True, right_index=True)

このようにして発生させたデータについて、単純に介入群と対照群の結果変数を比較すると下記になりました。(乱数で発生させているので、毎回結果は変わります)

介入群の結果変数の平均 対照群の結果変数の平均 介入群ー対照群
-3.30 -5.09 1.79

真の因果効果は、$Y = X_1+2X_2+3X_3+4X_4+Z$の$Z$の係数であることがわかっているので、今回のセレクションバイアスは$1.79-1=0.79$です。

傾向スコアの推定

　今回は傾向スコアの推定はロジスティック回帰モデルを用いて行います。

傾向スコアの推定
#ロジスティック回帰モデルのインスタンス作成
lr = LogisticRegression()

#ロジスティック回帰モデルの推定
lr.fit(df_result[cov_list_str], df_result["treatment_flg"])

#推定された傾向スコア
est_propensity_score = lr.predict_proba(df_result[cov_list_str])[:,1]

#傾向スコアをもとのデータフレームにマージ
df_estps = (
    pd.merge(
        df_result,
        pd.DataFrame(est_propensity_score, columns = ["est_propensity_score"]),
        how="left",
        left_index=True,
        right_index=True)
)

今回は、真の傾向スコアのモデルがロジスティック回帰モデルであることがわかっているので、モデルの評価は省略しますが、実務上では$AUC>0.7$であることが望ましいそうです。(ロジスティック回帰分析と傾向スコア解析)
今回シミュレーションで作ったデータフレームに含まれるカラムは下記です。

X1 X2 X3 X4 true_propensity_score treatment_flg result est_propensity_score
共変量 共変量 共変量 共変量 真の傾向スコア 介入変数 結果変数 傾向スコアの推定値

傾向スコアマッチング

最近傍マッチングで傾向スコアマッチングを実行するためのclass。クラス内のメソッドや引数の意味は後述します。

傾向スコアマッチングをするclass
#傾向スコアマッチング(最近傍マッチング)を実行するクラス
class propensityScoreMatching:
    #__init_で傾向スコアマッチングを行い、indexの組み合わせを取得する
    def __init__(self, df, cov_list, z, ps, rs):
        self.df = df
        self.cov_list = cov_list
        self.z = z
        self.ps = ps
        self.rs = rs


        #介入の有無でデータフレームを分割
        self.df0 = self.df[self.df[z] == 0]
        self.df1 = self.df[self.df[z] == 1]

        #df0のindex取得
        tmp_df0_index = self.df0[self.ps].index.values
        #マッチング後のindexを入れる変数を定義(介入なし)
        self.df0_index = np.empty(0, dtype="int64")
        #マッチング後のindexを定義(介入あり)
        self.df1_index = self.df1[self.ps].index.values

        #最近傍マッチングで傾向スコアマッチング
        for eps1 in self.df1[self.ps]:
            #介入ありと介入なしの傾向スコアの差の絶対値を計算
            abs_eps_list = [abs(eps1-eps0) for eps0 in self.df0[self.ps]]
            #傾向スコアの差の絶対値が最小のindexを取得
            min_index = tmp_df0_index[abs_eps_list.index(min(abs_eps_list))]
            #マッチング後のindexを入れる
            self.df0_index = np.append(self.df0_index, min_index)

    def get_effect(self):
        #各群の結果変数の平均を取得
        self.mean0 = np.average(self.df0.loc[self.df0_index][self.rs])  
        self.mean1 = np.average(self.df1.loc[self.df1_index][self.rs])

        return (self.mean1-self.mean0)

    def compare_cov_mean_var(self):
        #共変量調整後の共変量の平均
        self.cov_mean0 = np.mean(self.df0[self.cov_list].loc[self.df0_index])
        self.cov_mean1 = np.mean(self.df1[self.cov_list].loc[self.df1_index])

        #共変量調整前の共変量の平均
        self.not_cov_mean0 = np.mean(self.df0[self.cov_list])
        self.not_cov_mean1 = np.mean(self.df1[self.cov_list])

        #共変量調整後の共変量の平均の差
        self.adjusted_abs_diff_mean = abs(self.cov_mean1-self.cov_mean0)

        #共変量調整前の共変量の平均の差
        self.not_adjusted_abs_diff_mean = abs(self.not_cov_mean1-self.not_cov_mean0)  

        #作図
        ##パラメータ
        top = np.arange(len(self.adjusted_abs_diff_mean))
        height = 0.3
        ##作図関数
        #plt.subplot(1, 2, 1)
        plt.barh(top, self.adjusted_abs_diff_mean, label="adjusted", height=0.3, align="edge", zorder=10) 
        plt.barh(top+height, self.not_adjusted_abs_diff_mean, label="not adjusted", height=0.3, align="edge", zorder=10) 
        plt.yticks(top+height, self.adjusted_abs_diff_mean.index)
        plt.vlines([0.1], ymin=0, ymax=len(self.adjusted_abs_diff_mean), linestyle = "dashed")
        plt.ylim(0, len(self.adjusted_abs_diff_mean))
        plt.xlabel("Absolute Mean Differences")
        plt.ylabel("Covariate Balance")
        plt.legend(bbox_to_anchor=(1, 1), loc='upper right', borderaxespad=0, fontsize=8)

クラスに含まれるパラメータは下記の通りです。

クラスのパラメータ 意味
df 分析対象のpandas.DataFrame。
cov_list dfに含まれる共変量のカラム名。文字列のリストで与える。
z dfに含まれる介入変数のカラム名。文字列で与える。
ps dfに含まれる傾向スコアの推定値のカラム名。文字列で与える。
rs dfに含まれる結果変数のカラム名。文字列で与える。

また、メソッドの意味は下記の通りです。

クラスのパラメータ 意味
get_effect 傾向スコアマッチングによる因果効果の推定値を返す。マッチング方法は最近傍マッチング。
compare_cov_mean_var 傾向スコアマッチングによる共変量調整前後の共変量の平均のつり合いをみる。棒グラフを返す。

このクラスを実際に使うときのスクリプトは下記のようになります。

傾向スコアマッチングの実行
#インスタンス作成
match_result = (
    propensityScoreMatching(
        df = df_estps,               #対象のデータフレーム
        cov_list = cov_list_str,     #共変量のカラム名のリスト。cov_list_str = ["X1", "X2", "X3", "X4"]
        z = "treatment_flg",         #介入変数のカラム名
        ps = "est_propensity_score", #傾向スコアの推定値のカラム名
        rs = "result"                #結果変数のカラム名
    ) 
)

#因果効果の推定量計算
match_result.get_effect()

#平均の釣り合いの確認
match_result.compare_cov_mean_var()

結果は「シミュレーション結果」で報告します。

IPW推定量

IPW推定量を計算するためのclass。クラス内のメソッドや引数の意味は傾向スコアマッチングと同じです。

IPW推定量を計算するclass
#IPW推定量によって効果を算出するクラス
class inverseProbbilityWeight:
    #__init_でIPWを算出する
    def __init__(self, df, cov_list, z, ps, rs):
        self.df = df
        self.cov_list = cov_list
        self.z = z
        self.ps = ps
        self.rs = rs

        #介入の有無でデータフレームを分割
        self.df0 = self.df[self.df[z] == 0]
        self.df1 = self.df[self.df[z] == 1]

    def ipw(self, column):
        ipw1 = np.sum((self.df1[self.z]*self.df1[column])/self.df1[self.ps])/np.sum(self.df1[self.z]/self.df1[self.ps])
        ipw0 = np.sum(((1-self.df0[self.z])*self.df0[column])/(1-self.df0[self.ps]))/np.sum((1-self.df0[self.z])/(1-self.df0[self.ps]))       

        return(ipw1, ipw0)

    def get_effect(self):
        #各群のIPW推定量を計算
        self.ipw_mean1, self.ipw_mean0 = self.ipw(column=self.rs)

        return (self.ipw_mean1-self.ipw_mean0)

    def compare_cov_mean_var(self):
        #共変量調整後の共変量の平均の差の絶対値
        ipw_list = [self.ipw(cov) for cov in self.cov_list]
        self.adjusted_abs_diff_mean = [abs(ipw1-ipw0) for ipw1, ipw0 in ipw_list]

        #共変量調整前の共変量の平均の差の絶対値          
        ##共変量調整前の共変量の平均
        self.not_cov_mean0 = np.mean(self.df0[self.cov_list])
        self.not_cov_mean1 = np.mean(self.df1[self.cov_list])
        ##差の絶対値
        self.not_adjusted_abs_diff_mean = abs(self.not_cov_mean1-self.not_cov_mean0)

        #共変量調整前の共変量の分散の差
        self.not_adjusted_abs_diff_mean = abs(self.not_cov_mean1-self.not_cov_mean0)

        #作図
        ##パラメータ
        top = np.arange(len(self.adjusted_abs_diff_mean))
        height = 0.3
        ##作図関数
        #plt.subplot(1, 2, 1)
        plt.barh(top, self.adjusted_abs_diff_mean, label="adjusted", height=0.3, align="edge", zorder=10) 
        plt.barh(top+height, self.not_adjusted_abs_diff_mean, label="not adjusted", height=0.3, align="edge", zorder=10) 
        plt.yticks(top+height, self.cov_list)
        plt.vlines([0.1], ymin=0, ymax=len(self.adjusted_abs_diff_mean), linestyle = "dashed")
        plt.ylim(0, len(self.adjusted_abs_diff_mean))
        plt.xlabel("Absolute Mean Differences")
        plt.ylabel("Covariate Balance")
        plt.legend(bbox_to_anchor=(1, 1), loc='upper right', borderaxespad=0, fontsize=8)

このクラスを実際に使うときのスクリプトは下記のようになります。

IPW推定量の計算の実行
#インスタンス作成
ipw_result = (
    inverseProbbilityWeight(
        df = df_estps,               #対象のデータフレーム
        cov_list = cov_list_str,     #共変量のカラム名のリスト。cov_list_str = ["X1", "X2", "X3", "X4"]
        z = "treatment_flg",         #介入変数のカラム名
        ps = "est_propensity_score", #傾向スコアの推定値のカラム名
        rs = "result"                #結果変数のカラム名
        )               
)



#因果効果の推定量計算
ipw_result.get_effect()

#平均の釣り合いの確認
ipw_result.compare_cov_mean_var()

結果は「シミュレーション結果」で報告します。

カーネルマッチング

　classは作らず局所回帰をするためのメソッドを作成しました。まず最初にガウシアンカーネルとイパネクニコフ2次カーネルの定義をします。

カーネルの定義
## ガウシアンカーネル
def gaussianKernel(x, x_prime, width):
    k = np.exp(- np.linalg.norm(x - x_prime)**2 / (2 * width**2))
    return(k)

##イパネクニコフ2次カーネル
def epanechinikovKernel(x, x_prime, width):
    t = abs(x-x_prime)/width
    D = 3/4*(1-t**2) if abs(t) <= 1 else 0
    return(D)

引数の意味は下記です。

引数 意味
x 説明変数
x_prime 説明変数。xとx_primeの間の「距離」が大きいとカーネルは小さくなります
width バンド幅

次に局所回帰をするための関数を定義します。

局所回帰の実行
def localRegression(x, resvar, exvar, treatvar, df, kernel = "gaussianKernel", width = 0.1, dim = 1):

    #説明変数の行列作成
    X = np.ones(len(df[exvar]))
    for p in range(1, dim+1):
        xp = df[exvar]**p
        X = np.c_[X, xp]

    #カーネルが入った対角行列作成
    if kernel == "gaussianKernel":
        kernel_list = [(1-z_ele)*gaussianKernel(x, x_ele, width) for x_ele, z_ele in zip(df[exvar], df[treatvar])]
    elif kernel == "epanechinikovKernel":
        kernel_list = [(1-z_ele)*epanechinikovKernel(x, x_ele, width) for x_ele, z_ele in zip(df[exvar], df[treatvar])]
    else:
        print("please input kernel")
        return()

    W = np.diag(kernel_list)

    coef = np.linalg.inv((X.T)@W@X)@(X.T)@W@df[resvar]
    predict = np.sum(coef*[x**p for p in range(0, dim+1)])
    return(predict)

引数の意味は下記です。

引数 意味
x 説明変数
resvar 結果変数のカラム名。
exvar 傾向スコアの推定値のカラム名。
treatvar 介入変数のカラム名。
df 対照のpandas.DataFrame
kernel カーネル。gaussianKernel(ガウシアンカーネル)とepanechinikovKernel(イパネクニコフ2次カーネル)が選択可能。
width バンド幅
dim 局所回帰の説明変数の最大次数

関数たちは実装できたので、実際に局所回帰してみます！
まずは介入群と対照群にデータフレームを分割します。

介入群と対照群に分割
#介入群と対照群に分割する
df_estps1 = df_estps[df_estps["treatment_flg"] == 1]
df_estps0 = df_estps[df_estps["treatment_flg"] == 0]

次に、訓練データとテストデータに分割します。

訓練、テストデータに分割
df_estps0_train, df_estps0_test = train_test_split(df_estps0, test_size = size)

分割出来たら汎化性能の測定のために、局所回帰のハイパーパラメータを色々変えて局所回帰を実行してみます。
今回は、

  • カーネル：(ガウシアンカーネル,　イパネクニコフ2次カーネル)の2パターン
  • バンド幅：(0.1, 0.2, ..., 5.0)の50パターン
  • 局所回帰の説明変数の最大次数：(1, 2, 3, 4, 5)の5パターン

の全組み合わせで局所回帰を実行してMSEで評価しました。そのスクリプトがこちら。

汎化性能の測定
#対照群の訓練データを用いたモデルの作成とテストデータを用いた汎化性能の測定
##パラメータの候補を設定
kernel_list = ["gaussianKernel", "epanechinikovKernel"]
width_list = np.arange(0.1, 5.0, 0.1)
dim_list = list(range(1, 6))

##パラメータの全列挙パターン作成
param_list = itertools.product(kernel_list, width_list, dim_list)

##各パラメータについてMSEを計算

MSE_df = pd.DataFrame(columns=["kernel", "width", "dim", "MSE"])
for k, w, d, in param_list:
    ##テストデータの予測値作成
    predict_list = [
        localRegression(x = x_ele,
                        resvar = "result",
                        exvar = "est_propensity_score",
                        treatvar = "treatment_flg",
                        df = df_estps0_train,
                        kernel = k,
                        width = w,
                        dim = d)
        for x_ele in df_estps0_test["est_propensity_score"]
    ]

    #テストデータの真の結果
    result_list = df_estps0_test["result"]

    #MSEをパラメータとともに保存
    tmp_MSE = (
        pd.DataFrame(
            {"kernel" : [k],
             "width" : w,
             "dim" : d,
             "MSE" : mean_squared_error(predict_list, result_list)
            }
        )
    )

    MSE_df = MSE_df.append(tmp_MSE)

我が家のPCだと12分かかりましたが、なんとか終わりました。次にMSEが最小のパラメータを抽出します。

MSE最小のパラメータ出力
#MSEが最小のパラメータを出力
min_params_df = MSE_df[MSE_df["MSE"] == min(MSE_df["MSE"])]

今回は、

  • カーネル：ガウシアンカーネル
  • バンド幅：4.9
  • 局所回帰の説明変数の最大次数：5

のパターンのMSEが最小でした。このパラメータを使って、介入群のユーザが介入を受けなかった場合の結果変数を予測します。

予測値の計算
#選択されたモデルで介入群の介入がなかったときの結果変数を予測する
predict_list = [
    localRegression(x = x_ele,
                    resvar = "result",
                    exvar = "est_propensity_score",
                    treatvar = "treatment_flg",
                    df = df_estps0,
                    kernel = min_params_df["kernel"].item(),
                    width = min_params_df["width"].item(),
                    dim = min_params_df["dim"].item())
    for x_ele in df_estps1["est_propensity_score"]
]

最後に因果効果の推定量を計算します。

因果効果の推定値の計算
#因果効果を測定する
effect = np.mean(df_estps1["result"]-predict_list)

シミュレーション結果

　傾向スコアマッチング・IPW・カーネルマッチングの各手法によって得られた因果効果の推定量は下記のようになりました。

真値 セレクションバイアスが入った見せかけの効果 傾向スコアマッチング IPW カーネルマッチング
1.00 1.79 0.99 1.07 1.01

いずれの手法も真値である$1.00$に近い値となっており、セレクションバイアスを取り除くことができています。
また、傾向スコアマッチングとIPWについては、平均値の釣り合いを見ることもできます。
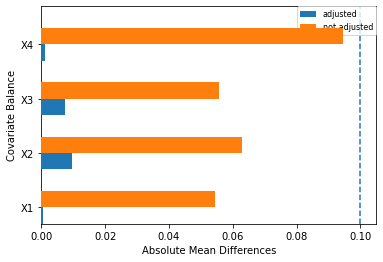
傾向スコアマッチングで共変量を調整した場合は下図のようになりました。
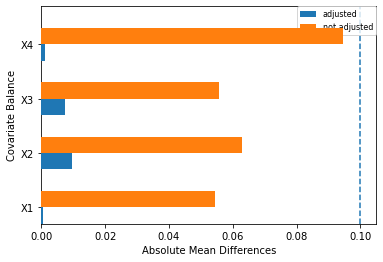
傾向スコアマッチング.png

また、IPWで共変量を調整した場合は下図です。
IPW.png

これらの図を見ると今回の場合は、X2についてはIPWの方が共変量の釣り合いがとれているものの、他の共変量については傾向スコアマッチングの方が釣り合いがとれています。したがって、今回の場合はIPWに比べて傾向スコアマッチングを選択したほうが良いとわかります。実際に、因果効果の推定値も傾向スコアマッチングは0.99であり、IPWの1.07よりも真値の1.00に近い値となっています。
　また、カーネルマッチングについては傾向スコアマッチングとIPWと比較することができないものの、因果効果の推定値は1.01となっており真値の1.00に近い値を取っています。

まとめ

　傾向スコアマッチング・IPW・カーネルマッチングの各手法の考え方と、pythonコードをまとめました。何かのお役に立てれば幸いです。

参考文献

  1. (1)式の右辺は傾向スコアがバランシングスコアであること、期待値繰り返しの公式を用いることで左辺と一致する。 ↩

  2. なんでこんな変てこりんな推定量が出てきたのかと思ったが、IPW推定量はM推定量の考え方から導出されている。また、直感的な説明は効果検証入門に載っていた。 ↩

  3. $V(\theta_0)$の具体的な式は書こうとしたが、煩雑になりすぎるのでやめた。 調査観察データの統計科学に記載がある。 ↩

17
16
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
17
16