はじめに
現在独学でRailsを勉強している初学者です。趣味で数値計算などにPythonを利用してます。
今回$n$が無限大のときの$n!$の相乗平均、つまり
\lim_{n \to \infty} \frac{\sqrt[n]{n!}}{n}\\
をPythonでなんとか求めていきたいと思います。
相乗平均って?
平均といえば、ある$n$個のデータ$x_1, x_2, ..., x_n$を全て足し合わせて$n$で割った値を求める相加平均を思い浮かべると思います。それに対し相乗平均$\mu$は
\mu = \sqrt[n]{x_1x_2...x_n}\\
で求めることができます。成長率や利率の計算などによく使われます。
本題
さて、前述で示したn!の相乗平均を求めていこうと思います。上式を使うと$\sqrt[n]{n!}$で求められますが、無限大に飛ばしたとき収束しなさそうなので$n$で除したものを無限大に飛ばしたときを考えます。つまり$\mu$が全体の何%の位置にあるか調べます。したがって
\lim_{n \to \infty} \frac{\sqrt[n]{n!}}{n}\\
を求めていきます。
解いてみる
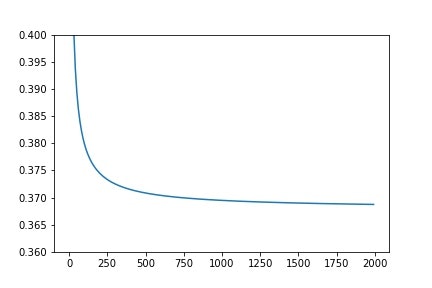
まず任意の数を$n$に代入してどの値に収束しそうなのか、matplotlibを使ってグラフをプロットしていきたいと思います。
sympyを使うと$2000!$でも楽々計算できます。標準モジュールのmathを使うと桁数が大きすぎるとエラーが返ってきます。
import matplotlib.pyplot as plt
import sympy
def fun(n):
n1 = sympy.factorial(n)
n2 = n1 ** (1/n)
n3 = n2/n
return n3
x = list(range(1,2000,10))
y = []
for i in x:
y.append(fun(i))
print(x)
print(y)
plt.plot(x,y)
plt.ylim([0.36,0.4])
グラフを見ると0.37あたりで収束しそうな気がします。
ここで上式がある値$a$に収束すると仮定します。また上式のままでは解きにくいので対数をとると、
\log \lim_{n \to \infty} \frac{\sqrt[n]{n!}}{n} = \log a\\
\lim_{n \to \infty} \log \frac{\sqrt[n]{n!}}{n} = \log a\\
整理すると、
\begin{align}
\lim_{n \to \infty} \log \frac{\sqrt[n]{n!}}{n} &= \lim_{n \to \infty} (\log {\sqrt[n]{n!}}-\log {n})\\
&= \lim_{n \to \infty} \Bigl( \frac{1}{n}\log {n!}-\log {n}\Bigr)\\
&= \lim_{n \to \infty} \Bigl( \frac{1}{n}\sum_{k=1}^{n} \log k-\log {n}\Bigr)
\end{align}\\
ここで
\sum_{k=1}^{n} \log k
について考えていきます。
区分級数の極限が出てきたらはさみうちの定理が利用できそうだと予想できます。ここで
\begin{align}
f(x) &= \log({x-1})\\
g(x) &= \log {x}
\end{align}
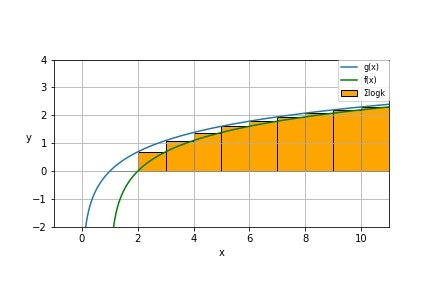
導入します。理由はこれから示します。以上3つの式を再度matplotlibを使ってプロットします。
with np.errstate(invalid='ignore'):
x = np.arange(-1, 11, 0.01)
y1 = np.log(x)
y2 = np.log(x-1)
fig = plt.figure()
plt.xlim([-1, 11])
plt.ylim([-2, 4])
plt.xlabel('x')
plt.ylabel('y', rotation=0)
plt.gca().set_aspect('equal')
plt.grid()
plt.plot(x, y1, label="g(x)")
plt.plot(x, y2, label="f(x)", color="green")
x = list(range(1,11,1))
y3 = []
for i in x:
y3.append(np.log(i))
print(y3)
plt.bar(x, y3, width = 1.0, align="edge",color="orange", edgecolor="black", label="Σlogk")
plt.legend(bbox_to_anchor=(1, 1), loc='upper right', borderaxespad=0, fontsize=8)
plt.show()
fig.savefig("log.jpg")
プロットを見てわかるように$\sum_{k=1}^{n} \log k$が$f(x)$と$g(x)$の積分値の間にあることがわかります。よって、
\int_{2}^{n}\log({x-1})dx< \sum_{k=1}^{n} \log k < \int_{2}^{n}\log {x} dx\\
上記の対数関数の定積分は部分積分を使えば解けます。しかしここではPythonを使っていくのが目的なので、
import sympy as sym
from sympy.plotting import plot
sym.init_printing(use_unicode=True)
from sympy import log
n, x, y = sym.symbols("n x y")
logx1 = log(x)
logx2 = log(x-1)
q1 = sym.integrate(logx1, (x, 2, n+1))
q2 = sym.integrate(logx2, (x, 2, n+1))
print(q1)
print(q2)
-n + (n + 1)*log(n + 1) - 2*log(2) + 1 #log(x)定積分の解
-n + (n + 1)*log(n) - log(n) + 1 #log(x-1)定積分の解
さらにそれぞれ$n$ で割って$\log {n}$引きます。つまり、最初の式に直します。
\frac{1}{n}-1< \frac{1}{n}\sum_{k=1}^{n} \log k-\log {n} < \log \Bigl(1+\frac{1}{n}\Bigr)+\frac{1}{n}\log(n+1)+\frac{1}{n}-\frac{2}{n}\log2-1\\
極限もsympy を使って求めます。
import sympy as sym
from sympy.plotting import plot
sym.init_printing(use_unicode=True)
from sympy import log
n, x, y = sym.symbols("n x y")
logx1 = log(x)
logx2 = log(x-1)
q1 = sym.integrate(logx1, (x, 2, n+1))
q2 = sym.integrate(logx2, (x, 2, n+1))
q11 = q1/n-log(n)
q22 = q2/n-log(n)
oo = sympy.oo
lim_q11 = sym.limit(q11, n, oo)
lim_q22 = sym.limit(q22, n, oo)
print(lim_q11)
print(lim_q22)
-1
-1
よってはさみうちの定理より、
\lim_{n \to \infty} \Bigl( \frac{1}{n}\sum_{k=1}^{n} \log k-\log {n}\Bigr)=\lim_{n \to \infty} \log \frac{\sqrt[n]{n!}}{n} = -1
\\
ところで、収束値を$a$とおきました。
\lim_{n \to \infty} \log \frac{\sqrt[n]{n!}}{n} = \log a\\
\begin{align}
a&= \lim_{n \to \infty} \frac{\sqrt[n]{n!}}{n}\\
&= \frac{1}{e}\\
&= 0.367...
\end{align}\\
お疲れ様でした。やっと収束が出ました。最初に適当な数字を代入して予測した収束値と合ってます。
自然対数$e$が出てくる美しい解です。
最後に
いかがでしたか?Pythonの数値計算用のモジュールを利用して解きましたが、もっとスマートな解き方もあると思います。またこの問題は高校数学の範囲内で解くことができます。
別解を考えてみるのも楽しいかもしれません。