こんにちは。Soohです。
今日の目標は、ARC118-D Hamiltonian Cycleを群論ベースの思考で解くことです。
ネタバレを含むので、それが嫌な人は先に問題を解いてからご覧になってください。
先に必要な知識をさらっていきますので、知ってる人は飛ばしてください。
群とは
非空の集合 $G$ について、$G$ 上の演算が定義されており以下の性質を満たすときに「$G$ は群を成す」と言います。
- 単位元 $e$ の存在
- 任意の元 $x \in G$ について逆元 $y \in G$ が存在し $ xy = e$ を満たす
- 演算が結合法則を満たす
例えば $ \mathbb{Z}$ は加法について群を成しています。
部分群とは
群 $G$ の部分集合 $H$ が $G$ と同じ演算により群を成す時、$ H $ を $G$ の部分群と呼びます。
また $ H $ が部分群の時、以下を満たします。
- $H$ の単位元と $G$ の単位元は一致、すなわち $e_H = e_G$
- $x \in H$ の逆元 $y\in H$ は $ G$ においても$ x$ の逆元である
証明は簡単です。
$e_H \in G$ であるから $e_He_G = e_H = e_He_H $ であり、$e_H \in G$ の逆元を左からかければ $e_G = e_H$.
2については $xy = e_H = e_G $ であることから分かります。
例えば、加法を演算として群 $ \mathbb{Z}$ は群 $ \mathbb{R} $の部分群です。
また、$ H (\subset G)$ が部分群であるかは次を満たせば良いです。
$$ \forall a,b \in H \implies a^{-1}b \in H $$
巡回群とは
ここら辺から後で効いてきます。
ある元 $ a \in G$ が存在して、任意の元 $ x \in G$ が $ x = a^{k} (k \in \mathbb{Z}) $ とかける時、$ G $ は $ a $ により生成された巡回群であるといい、$G = \langle a \rangle $ と書きます。
巡回群は可換群(群 + 交換法則)です。証明は次の通りです。
$ \forall x, y \in \langle a \rangle \implies x = a^{k}, y = a^{l}$
ゆえに $ xy = a^{k}a^{l} = a^{k+l} = a^{l}a^{k} = yx$
また、群 $G$ の部分群 $ H $ が巡回群である時、巡回部分群と呼びます。
例えば、$p$ を素数として$ (\mathbb{Z}/p\mathbb{Z})^{\times} $ は群です。($ \lbrace 1,2,\dots,p-1\rbrace$ の $ mod\space p$ 上の掛け算のことだと考えれば良いです。)
具体的に $p = 13 $ の時を考えると、$ \langle 3 \rangle = \lbrace 3, 9, 1 \rbrace$ となり、これは巡回部分群です。
良い性質としては $a^n = e$ なる $n$ は $\left| \langle a \rangle \right| $に一致します。これは $a$ の位数と呼ばれています。
左剰余類とは
群 $G$ とその部分群 $H$ を考えます。
$a \sim b \iff a^{-1}b \in H$ と定義すると $\sim$ は同値関係になります。
$ x \in G $ の同値類を $xH$ と書いて、これを $x$ による $H$ の左剰余類と呼びます。
この時定義から以下のようになります。
$$
\begin{eqnarray}
xH &=& \lbrace y\space |\space x^{-1}y \in H \rbrace \\ &=& \lbrace y \space | \space \exists h \in H, y = xh \rbrace
\end{eqnarray}
$$
このような左剰余類を集めたものを $G/H$ と書きます。数式に表すと以下のようになります。
$$
G/H = \lbrace xH \space | \space x \in G \rbrace
$$
言い換えれば「部分群 $H \subset G$ を決めて、 $ x,y\in G$ を取った時に $xH = yH$ となれば同じタイプの元だね〜〜」 と言って同じタイプの元を集めれば、いくつかの集合ができますね。そして、任意の $G$ の元はその集合のどれかに入ってるわけです。
次に超重要な性質があります。
$$ |xH| = |H| $$
詳細は省きますが、これは$H$ から $xH$ への全単射を構成することで証明ができます。
また、これから $ |H| $ は $|G|$ の約数であることも示せます。
本題
やっとこさ、下準備が終わりました。
ARC118-D Hamiltonian Cycle の問題概要はこうです。
- 素数 $P$ 及び整数 $1\le a,b \le P - 1$ が与えられる
- はじめ数列 $A$ は要素が1つだけで、それは $1$ である。
- 各ステップで $a,a^{-1}, b, b^{-1}$ から1つ選んで、Aの末尾にかけてAの新たな要素として加える
- 最終的に$ 2,3,...,P-1$がちょうど1度ずつ出現して、$A$ の末尾が $1$ となるようにせよ
まず $A_i$ がどのように表せるかを考えると $(\mathbb{Z}/p\mathbb{Z})^{\times}$ は可換群であるので、
$$ A_i = a^{k}b^{l} \ (k,l \in \mathbb{Z}) $$ の形になります。
以下では $a$ の位数を $d_a$ と表すことにします。
ここで巡回群 $ \langle b \rangle$ を考えてみましょう。
これは $(\mathbb{Z}/p\mathbb{Z})^{\times}$ の部分群です。「部分群とは」の末尾の判定法からすぐ分かります。
$ \langle b \rangle $ が部分群であることから左剰余類を考えることができます。
いま、$ A_i $ の形は $ a^{k}b^{l} $ に限定されていたので、この形をした左剰余類の集合 $S$ は
$$
\begin{eqnarray}
S &=& \lbrace a^i \langle b \rangle \space | \space i \in \mathbb{Z} \rbrace \\
&=& \lbrace a^i \langle b \rangle \space | \space 0 \le i < d_{a} \rbrace \quad (\because a^{d_a} = e)
\end{eqnarray}
$$
となります。
従って、答えが存在するには $(\mathbb{Z}/p\mathbb{Z})^{\times} $ $= \bigcup_{0 \le i < d_a} a^i \langle b \rangle $ であることが必要です。
しかし $ 0 \le x < y < d_a$ について $ a^{x} \langle b \rangle = a^{y} \langle b \rangle $ となることはあり得るし、実際に $1,2,\dots,P-1$ を全て動くのかも分からないので、どのように答えを構築すればいいか分かりません。
とりあえず $ a^k \in \langle b \rangle$ となる最小の $k\space (>0)$を取ります。
このとき次のことが言えます。
$$ 0 \le i,j < k, i\neq j \implies a^i \langle b \rangle \cap a^{j} \langle b \rangle = \phi $$
これは背理法で $k$ の最小性に矛盾させることで簡単に示せます。
また、次も言えます
$$
a^{x + k}\langle b \rangle = a^{x} \langle b \rangle \quad (\forall x \in \mathbb{Z})
$$
この証明も$ a^k \in \langle b \rangle $ から容易です。
以上のことから、$ 0 \le i < k $ のみを考えればいいことが分かります。
これと合わせて、「左剰余類とは」で述べた重要な性質から
$$ k\left| \langle b \rangle \right| = P - 1$$
でなければ答えが存在しないです。
逆に、この条件を満たす場合は必ず問題文の通りに構築することが可能です。
$P$ は素数であるので、$k$ または $\left |\langle b \rangle\right | $ は偶数となります。
従って、下の図(後者が偶数の場合の図)のようにジグザグしながら $1$ に戻ることが可能です。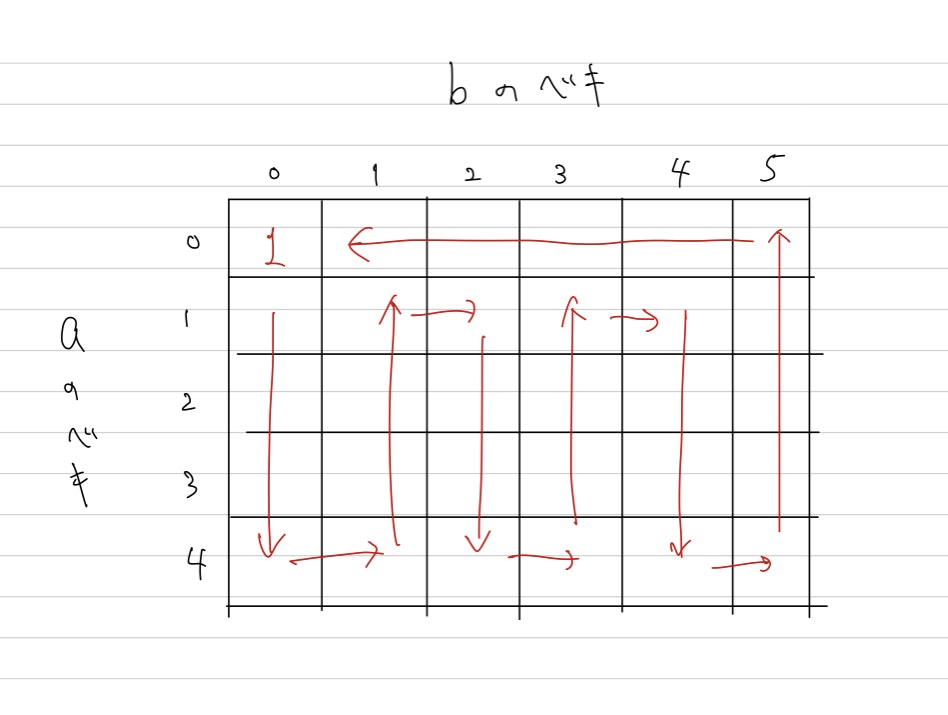
まとめ
群が必要だったかは分かりませんが、知識があると解法の証明がしやすいのかなぁと思いました。以上お疲れ様でした。
参考文献
雪江明彦, 代数学1 群論入門, 日本評論社, 2010