前回の記事でChirstopher Colah氏の記事「ニューラルネット、多様体、トポロジー」の中のいくつかの動画を再現しました。
シンプルな2値分離問題を学習する中で、ニューラルネットが入力データをどのように変換しながら、線形分離可能な状態へ持っていくかが直観的にわかるかと思います。
今回は、より詳細に「ニューラルネットの各層で何が起こっているのか」を見ていきたいと思います。
ニューラルネット各層の挙動
ニューラルネットの各層において、大きく二つの変換が実施されています。
- 全結合層でのアフィン変換
- 活性化関数による変換
式で表すと下記になります。
$$ \mathbb{h_2} = f(\mathbb{W} \mathbb{h_1} + \mathbb{b}) $$
$h_1$を一つ前の層の出力、$h_2$を次の層の出力とすると、まず全結合層において重みパラメータ行列$\mathbb{W}$による線形変換 とバイアスパラメータ $\mathbb{b}$による平行移動が合成されたアフィン変換が実施されます。その後、活性化関数$f$による非線形変換を行った上で次の層へと続いていきます。
ここでは、それぞれの変換がどのようなことを行っているかを視覚的に理解するため、入力2次元、出力2次元のシンプルな状況を考えてみます。よって、$\mathbb{W}$は2x2行列、$\mathbb{b}$は1x2のベクトルとなります。
1. アフィン変換
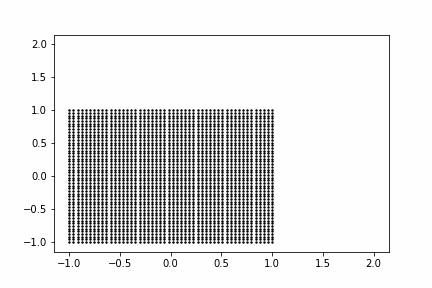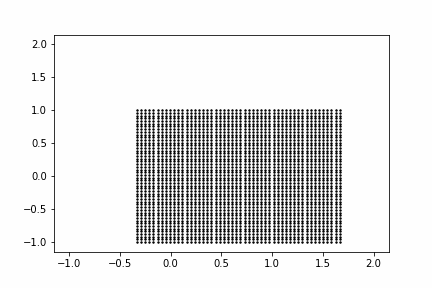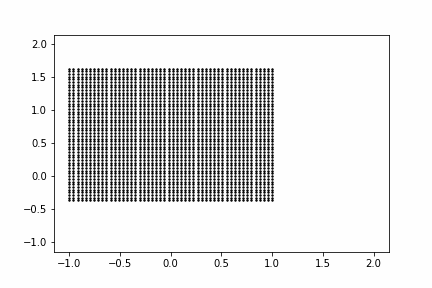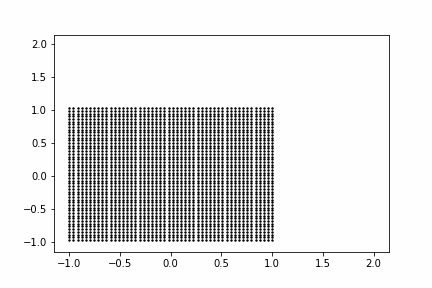
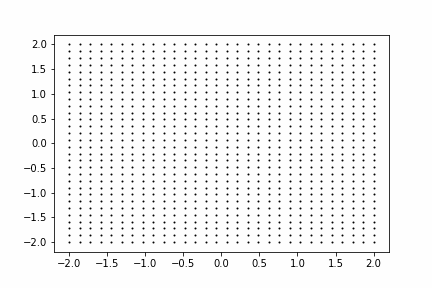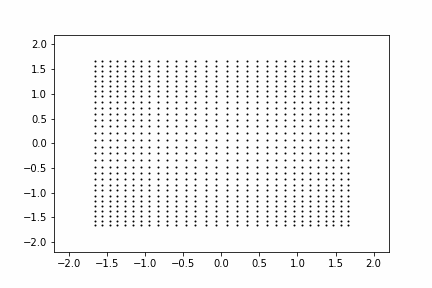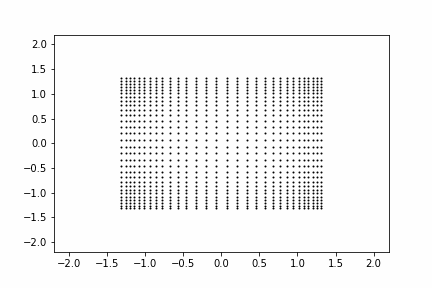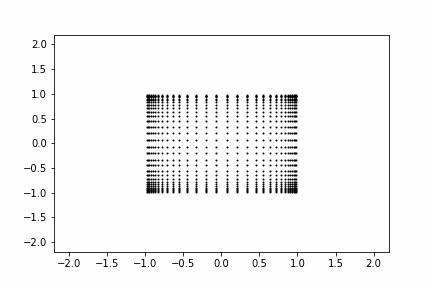
まずは線形変換$\mathbb{W} \mathbb{h_1}$を考えます。入力をシンプルな2次元のグリッド点として、線形変換がどのような変換を生成するかを動画にしてみました。
こちらは線形変換の中の特殊な一形態である回転行列による変換になります。
\mathbb{W}=\left[
\begin{matrix} \cos \theta & - \sin \theta \\ \sin \theta & \cos \theta \end{matrix}
\right]
$\theta$の値を変えることで元の座標を回転させることができます。
その他、行列の要素の値を変えることで、部分的に拡大したり縮小したりすることができます。ただし、動画にある通り中心点は変化させません。
一方でバイアスパラメータ $\mathbb{b}$は元の座標を平行移動させることができます。ここではy軸、x軸に平行な移動しかしていませんが、斜め方向の移動も可能です。
線形変換と平行移動を組み合わせたアフィン変換を施すことによって元の形状を引き伸ばしたり回転させたり移動させたりすることが可能になります。このような変換だけでもいろいろな問題を線形分離可能な形へと変換できることがイメージ湧くと思います。
2. 活性化関数による変換
アフィン変換を施した上で、更に非線形な変換を施すことでより難しい問題も解けるようにしているのが、活性化関数の役割になります。活性化関数にはいくつか種類がありますが、ここではよく使われる関数であるtanh(ハイパボリックタンジェント)関数とReLU関数について考察してみたいと思います。
tanh関数
tanh関数とは
$$tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}$$
で表される関数になります。グラフにすると下記になります。
ここで注目して頂きたいのが、tanhはx軸からy軸への写像(変換)を行っている点です。xの値がどんなに大きくても、yの値は1未満にしかなりません。また、xの値がどんなに小さくてもyの値は-1より大きい値になります。
よって、xの値の大きい部分を圧縮してゼロ近辺は(比較的)そのまま情報を保存して次の層へと渡すような変換が起きていることがイメージできるかと思います。
2次元グリッドのtanhによる変換を見るとそれがより具体的にイメージできます。中心部分(原点部分)は殆ど変化しませんが、周辺部分が縮小していきます。
ReLU関数
ReLU関数(ランプ関数とも呼ばれます)とは
ReLU(x) = \begin{cases}
0 & (x \le 0) \\
x & (x > 0)
\end{cases}
で表される関数になります。グラフにすると下記になります。
こちらも先ほどのtanhと同様xからyへの写像としてみなした場合、xが負の値を取る場合は0に圧縮し、それ以外はそのままxの値をyへ恒等写像する変換であることが分かります。
ある層から次の層に行く際に、負の値をすべてゼロに縮小してしまうことで、(逆説的に)プラスの部分の線形分離性を担保しようとしている、と理解することもできそうです。線形分離のために回転や圧縮拡大をする必要がない箇所(十分に分離できている箇所)をゼロに圧縮し、残っている部分に対してアフィン変換を実施していくことで線形分離性を高まていると捉えることができます。
ニューラルネット(深層学習)で行っていること
ここまでの考察は次元を圧縮したり拡大したりすることなく、同じ次元から同じ次元への変換でした。同様の考え方で、2次元の入力から3次元以上高次元空間へのアフィン変換と活性関数による変換が考えられます。2次元平面の座標点を、高次元空間上で回転させたり捻じ曲げたりすることで解くのが難しい問題を解けるようになる点が、「ユニット数を増やすこと」による意味です。
一方で、拡大・縮小・回転というアフィン変換による操作→活性化関数による非線形操作→アフィン変換による操作→活性化関数による非線形操作・・・という操作を何度も繰り返していくのが深層学習になります。直観的には、回転させて捻じ曲げて拡大して、、という独立した操作を連続して何度も実施することで複雑な表現を得ることができるのがイメージ湧くのでないでしょうか。
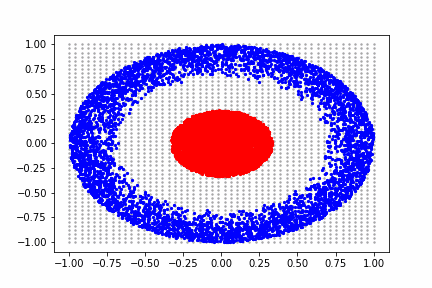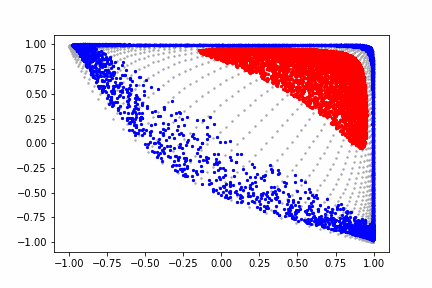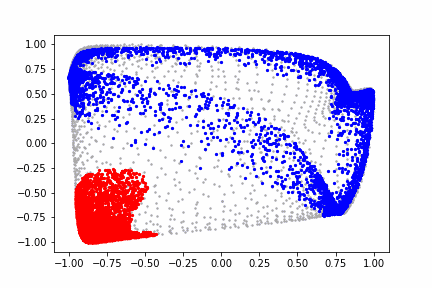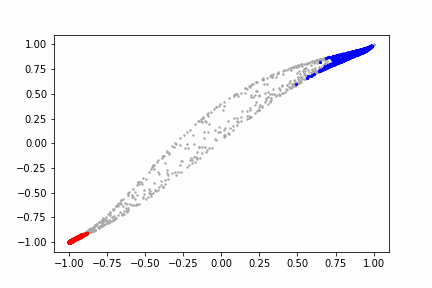
今まで考察したことの総まとめとして、前回の検討でも参照した2値分類問題「円とドーナツ」をニューラルネットで学習したいと思います。
前回はユニット数をかなり多めに設定(多次元への写像)しましたが、今回は2次元の分類問題を3次元に拡張して解くことをしたいと思います。
具体的には、下記のネットワークで学習していきます。
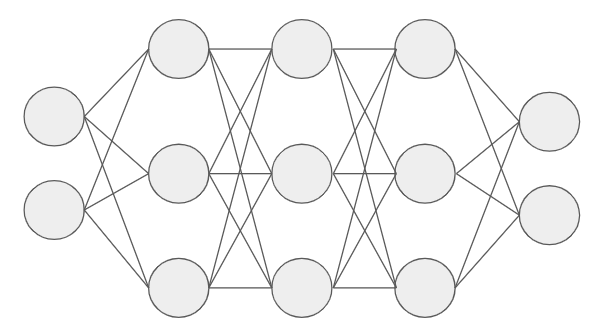
隠れ層:3層、各層のユニット数:3個なので、2次元の問題を3次元空間内で「アフィン変換し活性化関数による非線形変換」という操作を3回繰り返します。
活性化関数:tanh関数
前回と同様、活性化関数としてtanh関数を選択した場合の動画はこちらになります。
各層3次元に拡張していますが、絵の見やすさから2次元空間に射影した状態での可視化になります。
はじめに第1層のアフィン空間で少しずれながら斜めに回転していくことが見えます。その後第1回のtanh関数による変換で中心部分が拡大(実は周辺部分が縮小しているのをスケール合わせたために逆に見えている)していく様子が見えます。
その後第2層で回転と移動をしながら左下に赤い点が集まっていく様子が見えます。このようにアフィン変換による操作とtanh関数による操作を何回か繰り返すことで、赤エリアと青エリアがどんどん分離されていく点が良く分かるかと思います。
活性化関数:ReLU関数
次に、活性化関数をReLUに変更した場合を見てみたいと思います。
具体的な操作はもちろん異なるものの、アフィン変換で行われていることはもちろんtanh関数を選択した時と同じです。
活性化部分について、tanh関数の代わりにReLU関数を使うことによって、右上部分以外が「折り畳まれて」くことが見えると思います。面白いのは、2次元から2次元へのReLUによる写像では右下部分以外が「圧縮」されてしまうのに対して、高次元空間へ拡張した状態でReLU関数で写像した結果を2次元空間へ射影すると、拡張されて次元の自由度分だけ圧縮されていた部分にも値が残っており、その後のアフィン変換により回転されるとその残っていた次元が見えるようになり「折り畳まれていた」ことが分かります。実際は折り畳んでいる(ある次元の値が別の次元へと回転している)わけではなく、ある次元の値は0に収束している一方で、残っている次元の値は元のままであるため、正確には「次元がつぶされている」という表現が正しいかもしれません。
このような操作を繰り返すと、赤の部分がぐちゃっとつぶれた状態で集まってくるため、最終的に線形分離が簡単にできている点が面白いですね。tanh関数では赤の部分を拡大(赤以外の部分を縮小)することで赤部分の特徴を炙り出していましたが、ReLU関数を用いると、赤部分を集めて潰すことで赤部分の特徴を抽出しています。関数ととしてはまったく異なる形をしているものの、行っている操作は不思議な類似性があるなと思いました。
tanh関数とReLU関数の合成
活性化関数の挙動の違いを(なんとなく)理解したので、今度は混ぜてみました。
第1層:tanh関数、第2層:ReLU関数、第3層:tanh関数という形で活性化関数を混ぜることでどのような挙動が出るかを可視化しました。
はじめの活性化層で真ん中部分を拡大し、第2層の活性化層で折り畳んだ後、最後の層で再び間を拡大する様が見えます。
今回は簡単な問題(3次元に拡張したら簡単に解ける問題)だったのであまり大きな変化はなかったですが、難しい問題に対しては、元のデータ構造を理解することができれば、そのデータ構造を線形分離するのに効果的な活性化関数を選択できるようになるかもしれません。