前回、前々回と、ニューラルネットの挙動を理解するために色々アニメーションを作ってきました。
今回は、前回の検討に引き続き、ニューラルネットワークの中で非線形的な挙動を生み出す活性化関数について、面白い活性化関数がないか考察をしてみたいと思います。
活性化関数とは
ニューラルネットワークは、各隠れ層において「接続層での線形変換」に加えて、「活性化関数による非線形変換」を実施するネットワークになります。
もし活性化関数による非線形変換がない場合は、いくら隠れ層を増やしても表現力が増えません。(複数層の線形変換を1層の線形変換で表現できてしまう)よって、複雑な表現を手に入れるためには、活性化関数による非線形変換が重要なステップとなります。
活性化関数としてどのような関数であるべきかについては、下記のような要件が必要条件になるかと思います。
- 非線形であること
- 計算機で扱いやすい値を取ること(オーバーフロー対策)
- 微分が計算しやすいこと(必ずしも数学的に微分可能である必要はない)
非線形性の重要性については既に述べました。
計算機で扱いやすい値を取るかどうかはかなり重要かつ難しい問題です。たとえば、活性化関数として$f(x) = x^2$のような関数を使ってしまうと、入力 $x$の値が大きく(もしくは小さく)なってしまうと、出力が計算機で扱うには大きすぎる値になってしまう可能性があります。このような関数は計算の安定性の観点からも活性化関数としては推奨されません。
微分が計算しやすいことについては、ニューラルネットの学習が誤差逆伝播法にによって実行される以上満たすべき性質となります。計算量の重い遺伝的アルゴリズムや進化的計算を使う場合は必要条件になりませんが、(特に)深層学習のように非常にたくさんのパラメータを学習しなければならない状況においては勾配を使った学習以外はかなり難しいのが現状だと思います。
活性化関数いろいろ
前回の投稿では、代表的な活性化関数である、tanh関数とReLU関数について可視化しました。その他活性化関数として下記のようなものがあるそうです。想定以上に色々ありました。
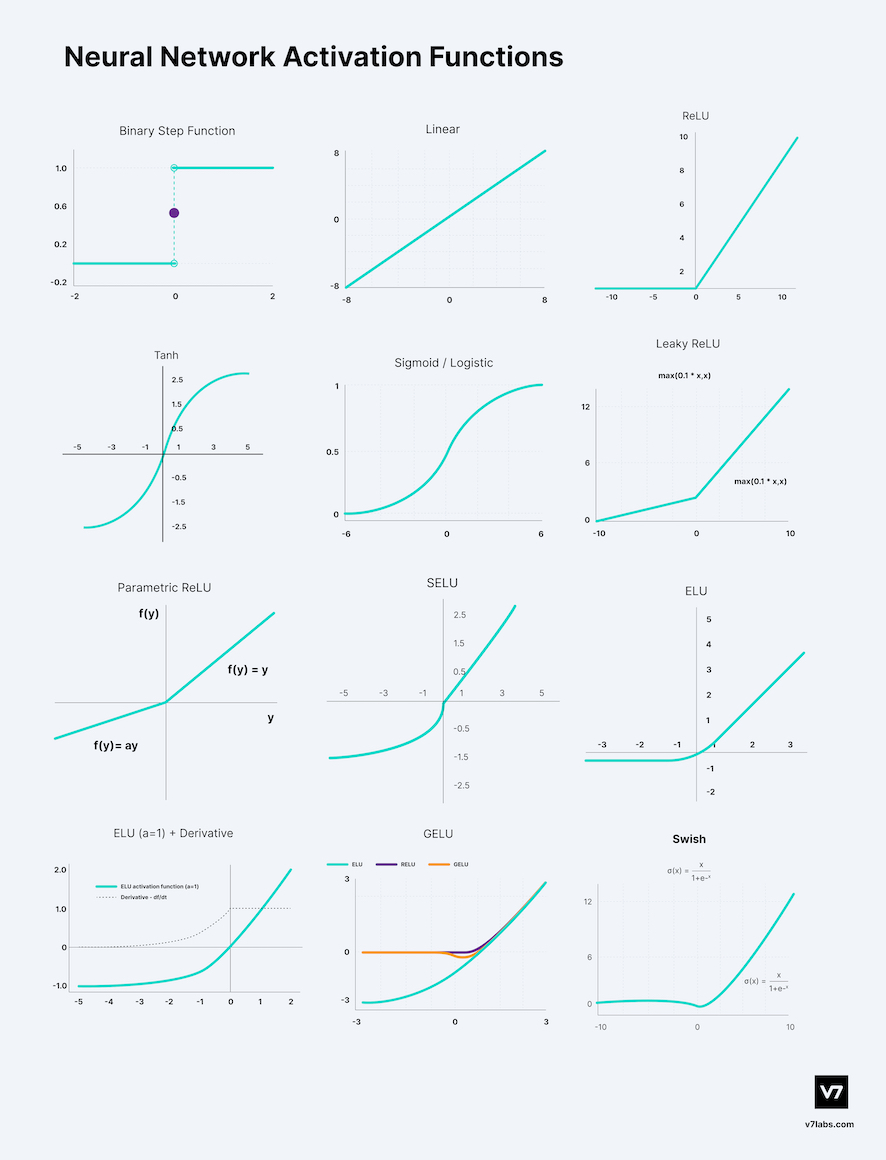
元ソース記事
こちらの記事にはもっとたくさんの活性化関数がまとまっていますのでご参照ください。
https://qiita.com/kuroitu/items/73cd401afd463a78115a
ただ、色々あるとはいえ、よく使われるのは2つのカテゴリに分けられそうです。
- S字型:シグモイド、tanh など
- キンク型:ReLU、LeakyReLU など
前回検討した通り、S字型活性化関数は、大きい値と小さい値の情報を潰して中央部分の値の情報を強く残す作用があります。一方で、キンク型はある閾値以下の値の情報を潰して、残りの情報を保存する効果があります。このように、活性化関数は次の層に移る際に「情報を取捨選択する」効果を持つと言えます。
詳しくは前回の記事をご参照ください。
https://qiita.com/Soichir0/items/b0b64ffd197c55a6ec54
活性化関数としてのsoftmax関数
もう少し変わった視点として、岡之原さんの著書「ディープラーニングを支える技術」で、softmax関数を活性化関数として記載していました。通常softmax関数は出力層の直前に使われることが多いですが、attention機構などでは隠れ層の一部の構成要素として使われています。
ということで、出力層ではなく、隠れ層の活性化関数としてsoftmaxを使った場合についてみてみたいと思います。
softmax関数とは厳密には関数ではなく、入力に対して一つ以上の値を返す写像になります。入力を$n$次元、出力を$m$次元とすると、softmax関数は$softmax: \mathbb{R}^n \rightarrow \mathbb{R}^m $として表せます。具体的には、入力ベクトルを$\mathbb{x} = (x_1, x_2, \dots ,x_n )$、出力ベクトルを$\mathbb{y} = (y_1, y_2, \dots ,y_m )$とした場合に、
$$ y_i = \frac{\exp(x_i)}{\sum_j \exp(x_j)}$$
と導出されます。
今までの活性化関数とは異なり、出力値が、複数の次元の入力値から出力されるため少し複雑な挙動を示すと考えられます。
前回と同様、まずは2次元ベクトル$(x_1, x_2)$を入力し、2次元ベクトル$(y_1, y2)$を出力してみました。入力と出力が同じ次元であるため、「入力の平面が出力時にどのように変形されるか」が可視化されます。
グリッド上に拡がっていた入力値が、直線に縮約してしまいました。考えてみれば当然で、softmaxは二つの値を入力すると、その二つの値の確率分布$p$、$1-p$を返すからです。
softmax関数は情報をかなり縮約してしまう効果があるので、恐らく通常のニューラルネット(MLP)における隠れ層の活性化関数としては使えなさそうだなと思います。
一応確認のため、前回と同様シンプルな問題セットアップにおいてsoftmax関数を隠れ層活性化関数にした場合にどのように入力空間が変化していくかを可視化してみました。
問題はシンプルな2値分類問題で、ある座標点が赤色か青色化を判別する問題です。モデルは隠れ層3のニューラルネットになります。
入力の次元平面が出力に近づくにつれてどのように線形可能な状態にまで変形していくかを可視化したいので、各層のユニット数は可視化可能な3次元までとしました。これ以上ユニット数を増やすと多次元空間上での空間の変換が可視化できないためです。
想定通り、学習は上手くいきませんでした。
折角2次元空間のリッチな情報を持っていたのに一つ目の隠れ層でそれを無理やり1次元に落とし込んでしまったため、赤部分と青部分がまざって潰れています。これではその後どのような線形変換、非線形変換をかませても上手くいきません。softmaxのような強力な情報縮約作用のある関数はMLPにおける隠れ層活性化関数には向かなそうですね。(もしかしたら、スキップ接続と組み合わせるなどといった手法だったら上手くいくかもしれませんので、時間があったら検討してみたいと思います。)
操作として面白そうな活性化関数
さて、世の中で検討されている活性化関数の中で、隠れ層でも使えそうなものはS字型とキンク型の2パターンがメジャーでしたが、「空間をどのように変形(操作)するか」という視点から、いくつかの活性関数候補を検討してみたいと思います。
① 絶対値
前回の検討で「ReLUが空間において値が正となる部分以外を潰す効果」がある点をみました。今回ただ潰すのではなく、「空間を折り畳む」という操作によって新しい表現ができないかなと考えてみました。イメージとして、右上と左上に同じパターンがある場合に、対角線で折りたたむことによってその同じパターンをまとめることができそうだなと思っています。
活性化関数としては、シンプルな関数を考えます。
$$absolute(x) = |x|$$
この関数なら、原点を中心にマイナス部分とプラス部分を折り畳む効果が見込めます。
また、冒頭で書いた活性化関数として最低限おさえるべき3条件も満たしています。
- 非線形であること
- 計算機で扱いやすい値を取ること(オーバーフロー対策)
- 微分が計算しやすいこと(必ずしも数学的に微分可能である必要はない)
ReLUのように、負の部分を潰すのではなく、正の部分と等値であるような変形をすることで、面白い表現を生み出せたらいいなと思います。
softmaxの時と同様のセットアップで隠れ層の活性化関数のみ変更した結果を動画にしました。
ニューラルネットの順伝播の過程で、空間がどんどん折り畳まれていくのが可視化出来ているかなと思います。誤差も十分小さくなり、きれいに線形分離可能な状況にもっていけてるのも良かったです。
空間を折り畳むという操作をできる活性化関数はこれまで無かったみたいなので、このような新しし表現方法が画像認識などの実問題でももしかしたら使えるかもしれません。
② 正弦波
考え方として、「折り畳む操作」に近いのですが、正弦波を活性化関数に使うのも良いかなと思いました。
$$sin(x) = \sin x$$
正弦波は入力に対して$[-1,1]$の値を行ったり来たりする出力を与えるので、何度も折り畳みを実行する感じになるかと思います。この活性化関数はSIRENと呼ばれるモデルを提唱した論文で使用されています。該当論文の解説記事はこちら。
2次元平面をこの関数で写像してみると下記になります。
基本的には各次元とも$[-1, 1]$に潰れていくのですが、潰れ方が波上になっているが少し見えるかと思います。
ただ、こちらの場合は絶対値とは異なり、かなり情報が圧縮されてしまっているので表現力という観点ではよくないかもしれません。
実際の2値分類問題を解いた結果がこちらになります。
想定以上に面白い結果になりました。空間を丸め込んだり、S字型に曲げたりするような操作が見て取れます。情報が圧縮されるといってもtanhと同じ値域なのでそれ程の心配はなさそうです。絶対値の場合ほどパキッと折り曲げることはもちろんできなかったですが、その代わり「空間をゆるく曲げる」という操作ができるのは、表現力という意味では面白いのではないでしょうか。
まとめ
今回はニューラルネットにおける非線形挙動を実現する活性化関数について考察してみました。現時点ではReLUが一番メジャーな活性化関数になっていますが、これは層がディープになるにつれて、活性化関数の非線形な表現力よりも、計算コストや微分のしやすさという点を優先しているからと思います。ニューラルネットの全体アーキテクチャで表現力を高めることができるので、活性化関数に求めることは「最低限の非線形性」くらいなのかもしれません。
ただ今回考察した通り、絶対値や正弦波のような活性化関数はあまり使われていないものの、非常に面白い表現力を持っている気がします。「活性化関数の表現力を最大限生かすアーキテクチャは何か」という視点でニューラルネットを構築すると面白いかなと思いました。









