あのアートの作り方 跳ね返り編 (Processing)

はじめに

これは「あのアートの作り方」の続編ですが、読んでなくても良いように書いている...はず。

この記事は「Processingやってみたくて、インストールしてみたはいいけどどういう風に作ればいいか分からない」という方のために書きました。
チュートリアルを通して、作品の基本となるコードや、(ゆるい)数学的な感覚を掴んでもらえると嬉しいなというものです。

つまりはProcessingのインストールと、基本的な文法の説明を割愛します。それでは行ってみましょう。

めちゃくちゃGIF画像を使っているので気を付けてください。通信量的に。

今回作ってみる作品

今回は (再び私の) この作品を作ってみましょう。

上のコードはp5.jsというProcessingのJavaScript版で書かれています。
これをProcessingのJava版に移植し、分かりやすくしたものが以下になります。

int frame=9000;
void setup() {
  size(500, 500);
}
void draw() {
  clear();
  noStroke();
  for (float y=0; y<600; y+=30) {
    for (int n=1; n<80; n++) {
      float angle = (frame+n)*noise(y)/40.0;
      float x = acos(cos(angle))/PI*500;
      float deltaY;
      if (sin(angle)<0) {
        deltaY = 50*sin(x/100*PI);
      } else {
        deltaY = 0;
      }
      circle(x, y+deltaY, 5);
    }
  }
  frame++;
}

キャンバスの作成 (再掲)

まず、これから作品を描くためのキャンバスを作ります。そのために、以下のコードを書きます。

void setup() {
  size(500, 500);
}

void draw() {
  clear();
}

実行結果：

これは、動きのあるスケッチを作るときにはほぼお決まりの文句なので、すらすらかけるようになっておくといいでしょう。
なお、size()に関しては好きな値でいいですが、ここでは 500x500 とします。

フレーム数を数える

これから、時間経過によって動きを変えるようにしたいので、そのために、時間をカウントする変数を追加します。

int frame=0; //<--追加

void setup() {
  size(500, 500);
}

void draw() {
  clear();
  
  noStroke();
    
  frame++; //<--追加
}

実行結果：変化なし

変数frameの内容は0から始まり、draw()関数が終了するたびにframeがひとつずつ増加していきます。結果として、frameには現在何フレームが経過したかの値が入ることになります。

もしかしたら、あなたは「frameCount でいいやんけ！」と思ったかもしれません。しかし、このように自分で変数を用意すると後で変更が容易になります。例えば「キーを押している間だけスケッチの速度が２倍になる」などの処理が簡単に実装できますし、実際、今回もそういう感じの変更を行います。

右に動く円を召喚する (x = frame)

まず、あの作品を作るには動く円を書くことが必要です。

int frame=0;

void setup() {
  size(500, 500);
}

void draw() {
  clear();
  
  noStroke();

  //x座標を少しずつずらす
  float x=frame;
  circle(x, 250, 5);
  
  frame++;
}

実行結果：

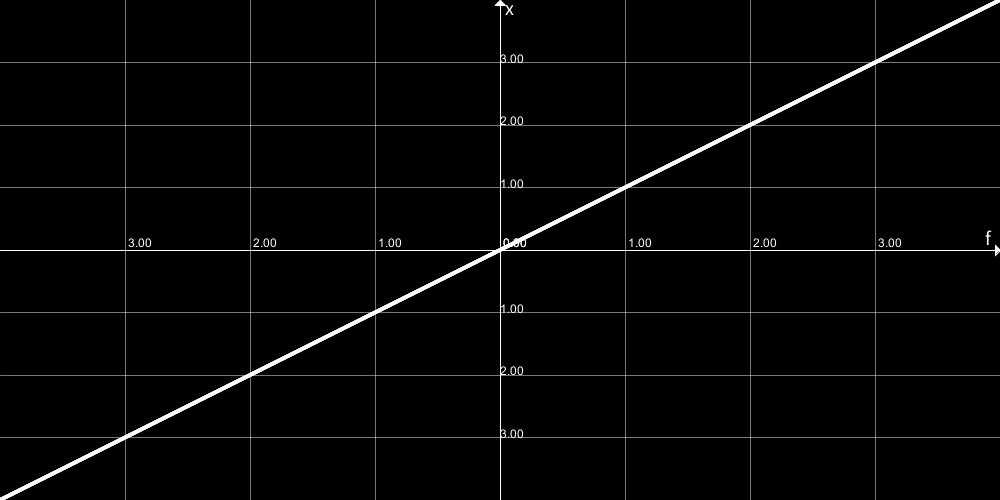
このようにx座標をframeに応じて増やすことによって、「経過したフレーム数が大きくなるほど大きいx座標に」円を書くことができます。

ところで、これは見方を変えると、x = frameという関数によってx座標が決まっているともいうことができますね？グラフにしてみるとこんな感じです：

円を行ったり来たりするようにする (x = acos(cos(frame)))

これに関してはまず見てもらった方が早そうな。

int frame=0;

void setup() {
  size(500, 500);
}

void draw() {
  clear();
  
  noStroke();

  //x座標を左右に行ったり来たりさせる
  float angle = frame/40.0;
  float x=acos(cos(angle))/PI*500;
  circle(x, 250, 5);
  
  frame++;
}

実行結果：

実際は円を左右に行ったり来たりさせたいので、上下にカクカク動く関数、いわゆる三角波が必要です。
x = **acos(cos(frame))**という関数を用いるとそれを実現することができます。

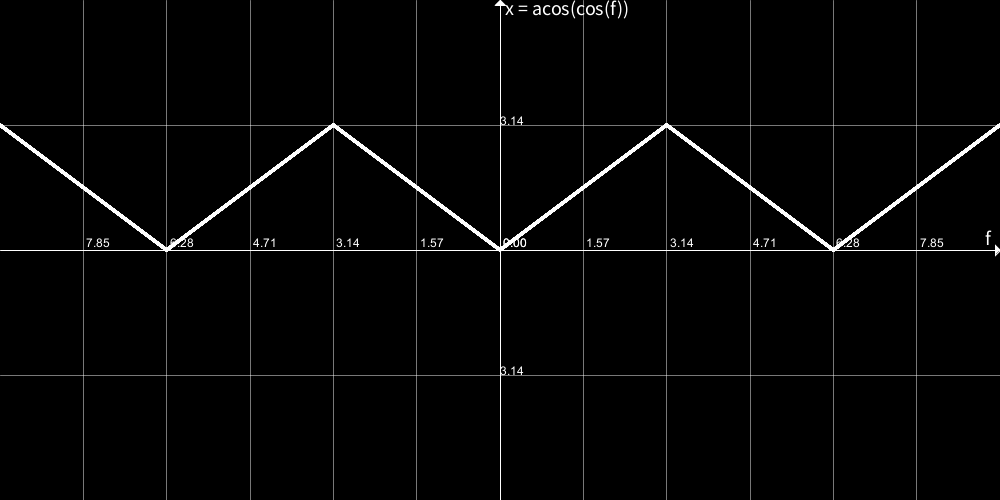
ただ、このままでは変化が速すぎ、かつ、小さすぎなので、それを調整してやる必要があります。
つまり、周期と振幅を調整する、ということですね。前回の記事 が参考になるかもしれません。

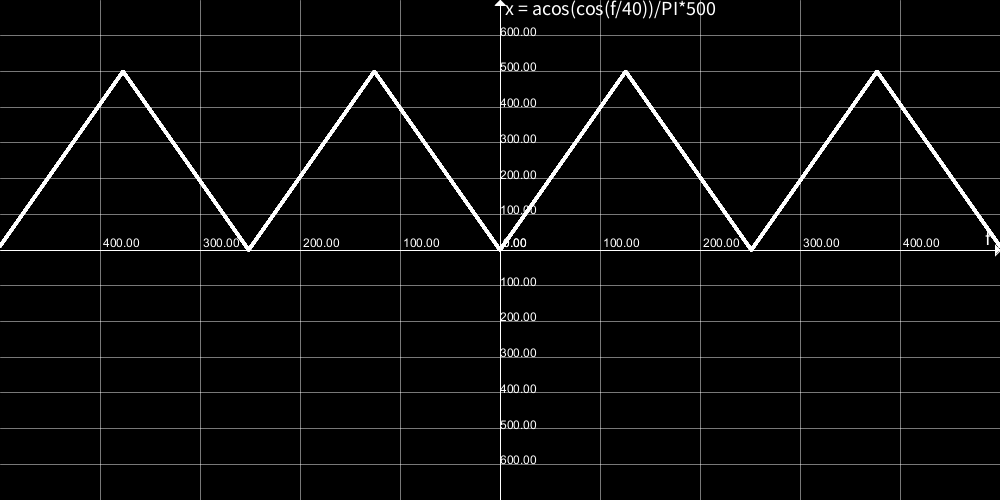
いい感じの調整を施したのが以下になります。(目盛りが変わっていることに注目)

実際は「書いて動かす」を繰り返すことによっていい感じの数値を探しました。

これを circle() のx座標に対応させることで円を左右に行ったり来たりさせることができます。
ちょっと複雑なので、 cos() の引数を angle として外に出しておきました。

円を並べて線にする

小さい円をたくさん並べると一つの線のようになります。(参考：前回の記事)
円が一つだけでは少し寂しいので、1フレームずつずれた円を書いていくことによって"少しだけずれた"円をつなげて、一つの線にしたいと思います。

int frame=0;

void setup() {
  size(500, 500);
}

void draw() {
  clear();
  
  noStroke();

  for(int n=1;n<80;n++){
    //frameのかわりに "frame+n" を使う
    float angle = (frame+n)/40.0;
    float x=acos(cos(angle))/PI*500;
    circle(x, 250, 5);
  }
  
  frame++;
}

実行結果：

frame を frame + n に置き換えました。こうすることで、フレーム数が n だけずれた時間の円を書くことができるようになります。そして、nをfor文でたくさん用意すれば、その数の円がつながっていくのです！

例えばn=1の時は (n=0の時と比べて) 1フレームだけ後、n=2なら2フレーム後、っていう様に１フレームずつずれていきます。

このようにたくさん円をつなげることで、一つの線になっているように見えるのです。

線を曲げる

ここであなたは何故か線を曲げたくなる衝動に駆られました。では、線をぐにゃぐにゃに曲げてみましょう。

int frame=0;

void setup() {
  size(500, 500);
}

void draw() {
  clear();
  
  noStroke();

  for(int n=1;n<80;n++){
    float angle = (frame+n)/40.0;
    float x=acos(cos(angle))/PI*500;
    //yの変化する分
    float deltaY = 50*sin(x/100*PI);
    circle(x, 250 + deltaY, 5);
  }
  
  frame++;
}

実行結果：

まず、deltaYという新しい変数を用意して、元々のy座標からいくらずらすか、を入れておきます。ここでは、50*sin(x/100*PI)という式を用意しました。これは、sin(x) に"いい感じの調整"をしたものになります。これをもちいると、xの値に応じて線を滑らかに曲げる、ということができます。 (参考：前回の記事)

これと元々のy座標を足したものをcircleの新しいy座標とすることによって、この波を生み出すことができます。

補足：後の為に、x=0 か x=500であるような点ではdeltaY=0でなければなりません。そうしなければ端で中心からずれてしまい、折り返しの際に円の"瞬間移動"が起きてしまいます。変えて遊んでみるときは注意です。

折り返しの時は線を真っすぐにする

あなたは変化を幾分かつけるために、線が折り返してきたときに真っすぐにしていきたいと思いました：

int frame=0;

void setup() {
  size(500, 500);
}

void draw() {
  clear();
  
  noStroke();

  for(int n=1;n<80;n++){
    float angle = (frame+n)/40.0;
    float x=acos(cos(angle))/PI*500;
    float deltaY;
    //sin(angle)によってdeltaYを変える
    if (sin(angle)<0) {
      //ぐねぐねモード
      deltaY = 50*sin(x/100*PI);
    } else {
      //直線モード
      deltaY = 0;
    }
    circle(x, 250 + deltaY, 5);
  }
  
  frame++;
}

実行結果：

deltaYが0のとき、基準のY座標からのずれがずっと0になるので、結果的に、(折り返し中の)全ての円が同じY座標を持つため、真っすぐの線になります。(「円を行ったり来たりするようにする」の章でのコードが、まさにdeltaY=0の状態です。)

ですから、xが増えているか減っているかどうかによってdeltaY=0と、deltaY = 50*sin(x/100*PI)をいい感じに切り替えていけば、動きが変えられます。

では、 **xが増えている・減っている、どちらなのか。**どう知ればいいのでしょうか？
たぶんx の動きは cos(angle)と似てるんじゃないかなーと思って調べると：

「cos(angle) が増加するならacos(cos(angle))が減少する。」

よって、単純にcos(angle)の増加・減少を考えれば、xの増加・減少を知ることができます。

・・・で、
cos(angle)の増加・減少は微分によって知ることができ、cos(angle)の微分はおおよそsin(angle)なので、それが0より大きいか、小さいかによって分岐させればよいことになります。その判定をしている部分がif (sin(angle)<0)なのです。

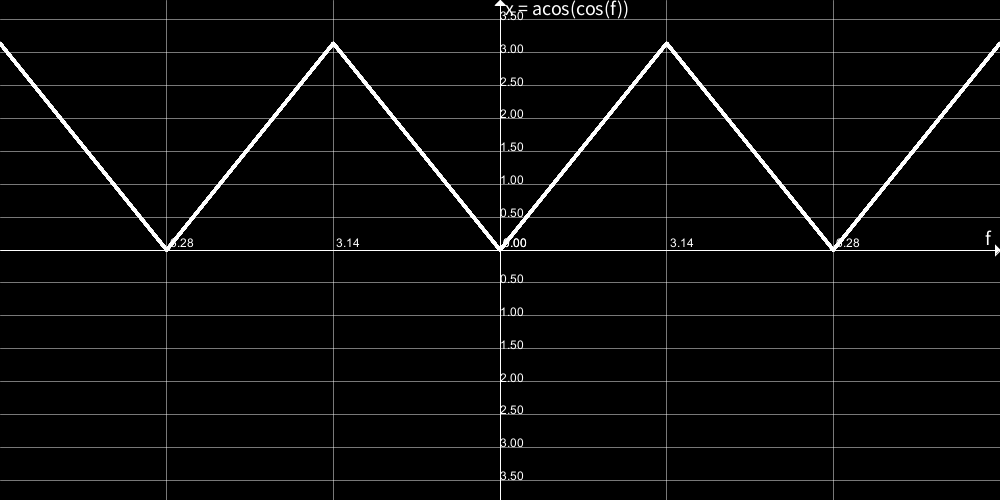
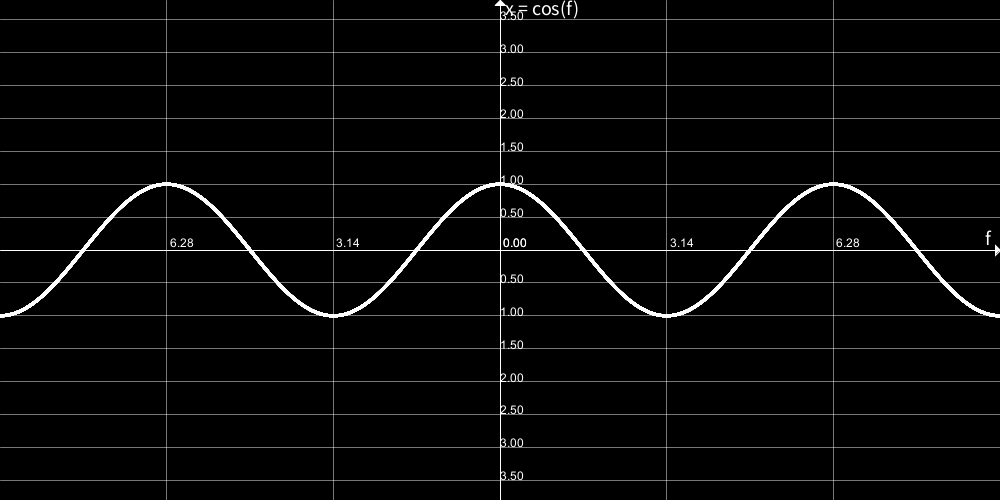
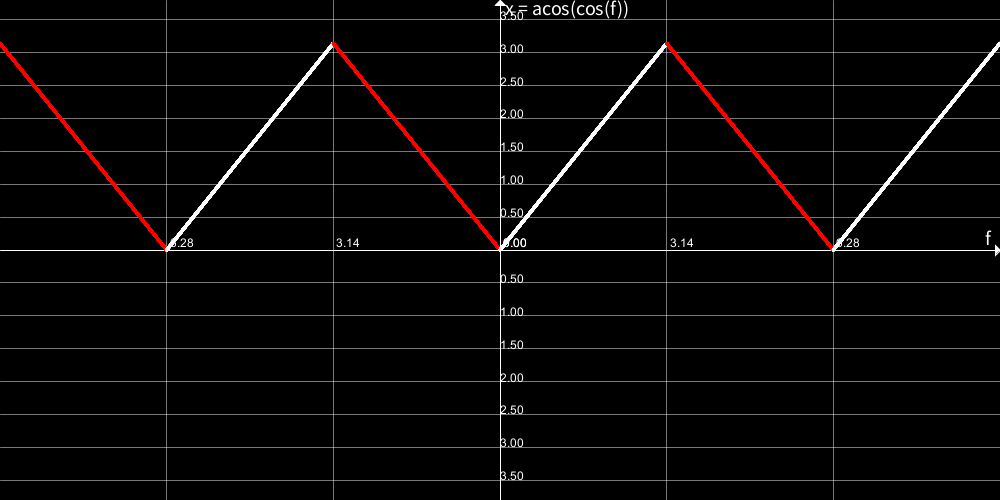
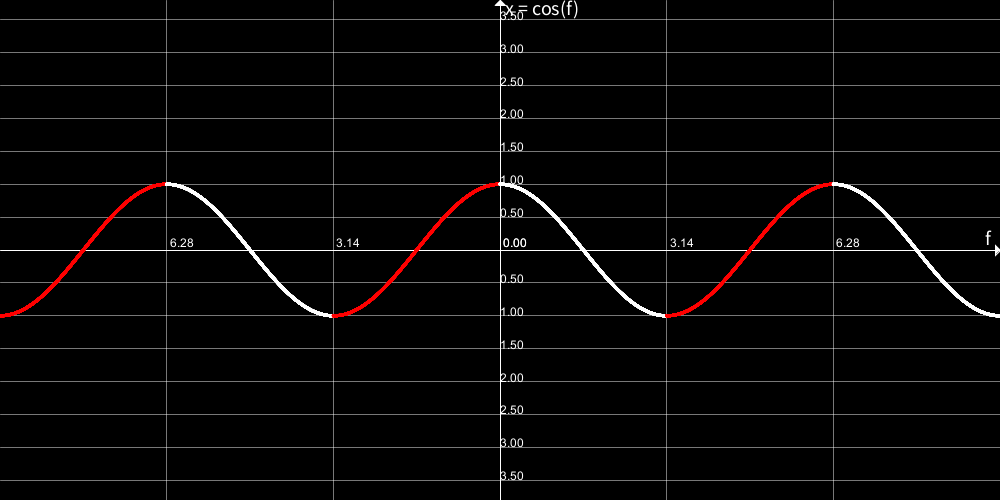
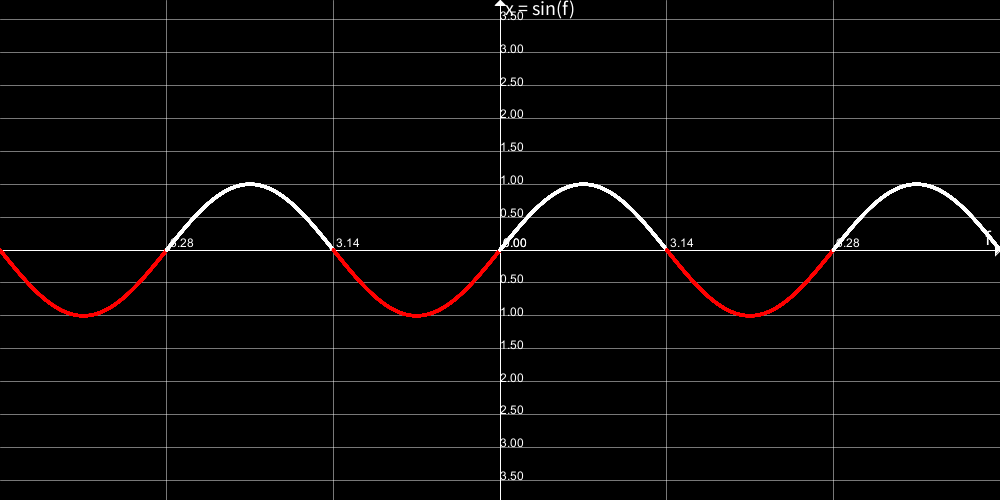
少々難しいですが、参考までにacos(cos(angle))とcos(angle)とsin(angle)のグラフを貼っておきます。
sin(angle)<0の部分に着色しておきました。

acos(cos(angle))、つまりxが減少傾向の時に、sin(angle)は0より小さくなる、ということが分かってもらえたでしょうか。

線を増やす

これまでで、おおよそのギミックは終わりましたが、線が一本じゃさみしいので増やしていきたいですよね。

int frame=0;

void setup() {
  size(500, 500);
}

void draw() {
  clear();
  
  noStroke();

  //基準のy座標をたくさん用意する
  for (float y=0; y<600; y+=30) {
    for(int n=1;n<80;n++){
      float angle = (frame+n)/40.0;
      float x=acos(cos(angle))/PI*500;
      float deltaY;
      if (sin(angle)<0) {
        deltaY = 50*sin(x/100*PI);
      } else {
        deltaY = 0;
      }
      //250をyに変更
      circle(x, y + deltaY, 5);
    }
  }
  
  frame++;
}

実行結果：

今まではy=250を基準としていましたが、その基準をたくさん用意することで線を並べることが出来ました。

y座標ごとに線の進行速度を変える

全部同じ動きの線ではつまらないので速度を変えます。

int frame=0;

void setup() {
  size(500, 500);
}

void draw() {
  clear();
  
  noStroke();

  for (float y=0; y<600; y+=30) {
    for(int n=1;n<80;n++){
      //基準のy座標によって速度を変える
      float angle = (frame+n)*noise(y)/40.0;
      float x=acos(cos(angle))/PI*500;
      float deltaY;
      if (sin(angle)<0) {
        deltaY = 50*sin(x/100*PI);
      } else {
        deltaY = 0;
      }
      circle(x, y + deltaY, 5);
    }
  }
  
  frame++;
}

実行結果：

noise関数はその引数によって異なる値を返します。 (参考：前回の記事)

ですから、(frame+n)を、(frame+n)*noise(y)に置き換えることで、angleの増加する速さがyによって変化します。結果的に、xの変化する速さがyによって変わることになります。

開始時刻を八百長する (ほとんど再掲)

速度は変えることができましたが、開始時点では結局全部同じ位置からスタートしてあまり美しくないので、バラバラの位置から開始するようにします。

//時刻ずらし
int frame=9000;
void setup() {
  size(500, 500);
}
void draw() {
  clear();
  noStroke();
  for (float y=0; y<600; y+=30) {
    for (int n=1; n<80; n++) {
      float angle = (frame+n)*noise(y)/40.0;
      float x = acos(cos(angle))/PI*500;
      float deltaY;
      if (sin(angle)<0) {
        deltaY = 50*sin(x/100*PI);
      } else {
        deltaY = 0;
      }
      circle(x, y+deltaY, 5);
    }
  }
  frame++;
}

実行結果：

位置をずらすといっても、速度が既にバラバラなので、十分な時間がたった後なら、開いている場所もバラバラであるといえますね。
よって、スケッチを動かす前に、十分な時間を予め経過したものにします。
このためには単に経過時間を表すframeに9000を先に入れておきます。

こうすれば9000フレーム経過した地点から回転が始まるのでさすがにバラバラになっていますね。

これにて完成です！

あとがき

もしかしたらやっぱり前の記事を読んでいないと理解が難しいかもしれない(ぉ

この記事を読んで下さりありがとうございました！