あのアートの作り方 (Processing)

はじめに

この記事は「Processingやってみたくて、インストールしてみたはいいけどどういう風に作ればいいか分からない」という方のために書きました。
チュートリアルを通して、作品の基本となるコードや、(ゆるい)数学的な感覚を掴んでもらえると嬉しいなというものです。

つまりはProcessingのインストールと、基本的な文法の説明を割愛します。それでは行ってみましょう。

今回作ってみる作品

今回は (私ので申し訳ないですが) この作品を作ってみましょう。

上のコードを分かりやすくしたものが以下になります。

void setup() {
  size(500, 500);
}
// フレーム数
float frame = 9000;
void draw() {
  clear();
  noStroke();
  for (float radius = 0; radius < 400; radius += 30) {
    for (float angle = 0; angle < PI*1.5; angle += 0.01) {
      // 変化させたパラメーター
      float adjustedAngle = angle + frame / 30 * noise(radius);
      float adjustedRadius = radius + 9 * sin(adjustedAngle * 8 + radius);
      circle(250 + adjustedRadius * cos(adjustedAngle), 250 + adjustedRadius * sin(adjustedAngle), 5);
    }
  }
  frame++;
}

キャンバスの作成

まず、これから作品を描くためのキャンバスを作ります。そのために、以下のコードを書きます。

void setup() {
  size(500, 500);
}

void draw() {
  clear();
}

実行結果：

これは、動きのあるスケッチを作るときにはほぼお決まりの文句なので、すらすらかけるようになっておくといいでしょう。
なお、size()に関しては好きな値でいいですが、ここでは 500x500 とします。

円と線

円は、円を描くためだけの道具ではなく、線を描くのに使うこともできます。では、それを試してみましょう。

void setup() {
  size(500, 500);
}

void draw() {
  clear();
  
  noStroke();
  
  // x座標が0から500の間で、y座標が250の位置に大きさ5の円を描く。
  for(float x=0; x<500; x++){
    circle(x, 250, 5);
  }
}

実行結果：

ここでは、小さな円を横一列にずらーっと並べることによって線を形成しています。横に並べるときに邪魔になるので、 noStroke() によって円の枠線を消しています。

円と円 (重要)

円と線 と同様の要領で、円を描くこともできます。

void setup() {
  size(500, 500);
}

void draw() {
  clear();
  noStroke();
  
  //角度が0からTAUの間で、半径100の位置に大きさ5の円を描く。
  for(float angle = 0; angle<TAU; angle += 0.01){
    float radius = 100;
    circle(250+radius*cos(angle), 250+radius*sin(angle), 5);
  }
}

実行結果：

特に重要なのが、circle()の座標指定です。まず以下の事を知っておく必要があります。

• 点 (centerX, centerY) から、角度 angle の方向へ、距離 radius だけ進んだ位置の座標は以下で求めることができる。

(centerX + radius * cos(angle), centerY + radius * sin(angle))

よって、上のコードでは、キャンバスの中心である点(250,250)から、全方向(ラジアンなので0～TAU)に、radiusだけ離れた位置に円を描いています。こうすることによって、大きな円を作成することができます。

TAU は、 2π のことで、 2 * PI と同じです。

円を増やす

一個だけの円では味気ないので数を増やします。

void setup() {
  size(500, 500);
}

void draw() {
  clear();
  noStroke();

  //半径の変化
  for (float radius = 0; radius < 400; radius += 30) {
    //角度が0からTAUの間で、半径radiusの位置に円を描く。
    for (float angle=0; angle<TAU; angle += 0.01) {
      circle(250+radius*cos(angle), 250+radius*sin(angle), 5);
    }
  }
}

実行結果：

先ほどは半径をべた書きしていましたが、for文で全体を囲い、半径を徐々に増やしながら描画していくことで円を増やすことができますね。

円に穴を開ける

全方向だと少し窮屈な感じがするので、円を途切れさせます。

void setup() {
  size(500, 500);
}

void draw() {
  clear();
  noStroke();

  //半径の変化
  for (float radius = 0; radius < 400; radius += 30) {
    //角度が0からPI*1.5の間で、半径radiusの位置に円を描く。
    for (float angle=0; angle<PI*1.5; angle += 0.01) {
      circle(250+radius*cos(angle), 250+radius*sin(angle), 5);
    }
  }
}

実行結果：

もちろん、円を描画する角度であるangleの最大値を変更すると、一部分だけを描画できるようになります。
もともとは0～2πまで動かして円を描いていましたが、1.5πまでにすることで、線の長さを少し短くしています。

パラメーター調整の準備

ここまでだと、「円をわざわざひとつずつ描かなくてもarc()でいいやんけ！」と思ったかもしれません。しかし、この描画方法の本領はここからです。この段階では、その準備をします。

void setup() {
  size(500, 500);
}

void draw() {
  clear();
  noStroke();

  //半径の変化
  for (float radius = 0; radius < 400; radius += 30) {
    //角度が0からPI*1.5の間で、半径radiusの位置に円を描く。
    for (float angle=0; angle<PI*1.5; angle += 0.01) {
      //パラメータの調整
      float adjustedAngle = angle;      
      float adjustedRadius = radius;
      circle(250 + adjustedRadius * cos(adjustedAngle), 250 + adjustedRadius * sin(adjustedAngle), 5);
    }
  }
}

実行結果：変化なし

新たにadjustedAngleとadjustedRadiusを追加しました。(意味はそれぞれ、「調整された角度」「調整された半径」です。)
また、その変数を使ってcircle関数の引数を書き換えました。
今、circle関数では、「点(250, 250)から、adjustedAngleの方向に、adjustedRadiusだけ離れた位置に、大きさ5の円を描画する」という処理が行われるようになりました。

つまり、adjustedAngleやadjustedRadiusを変化させれば、線を曲げたり、線を動かしたりすることができます。これはarc()にはない強みです。

(現在はangleやradiusをそのまま使っているために実行結果には変化はありません。)

線を曲げる

ここであなたは何故か線を曲げたくなる衝動に駆られました。では、円の線をぐにゃぐにゃに曲げてみましょう。

void setup() {
  size(500, 500);
}

void draw() {
  clear();
  noStroke();

  //半径の変化
  for (float radius = 0; radius < 400; radius += 30) {
    //角度が0からPI*1.5の間で、半径radiusの位置に円を描く。
    for (float angle=0; angle<PI*1.5; angle += 0.01) {
      //パラメータの調整
      float adjustedAngle = angle;
      //sin()を追加
      float adjustedRadius = radius + sin(adjustedAngle);
      circle(250 + adjustedRadius * cos(adjustedAngle), 250 + adjustedRadius * sin(adjustedAngle), 5);
    }
  }
}

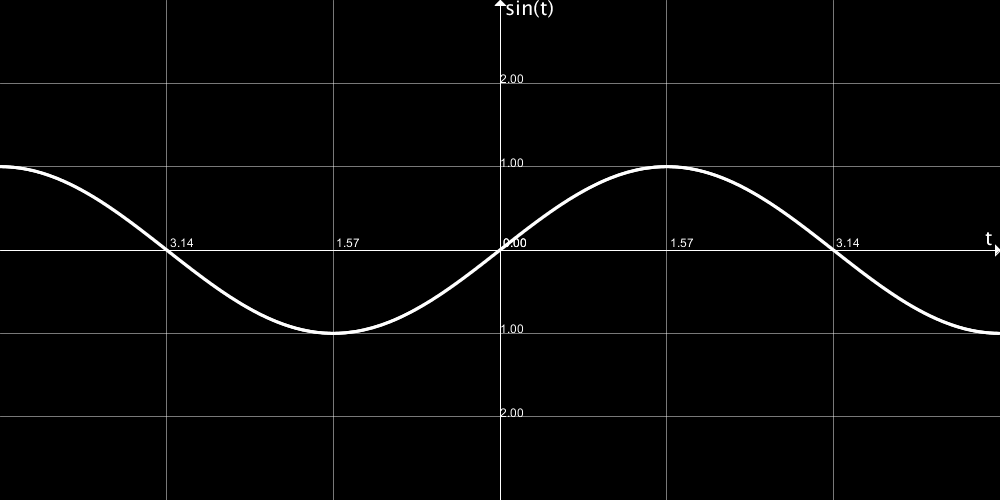
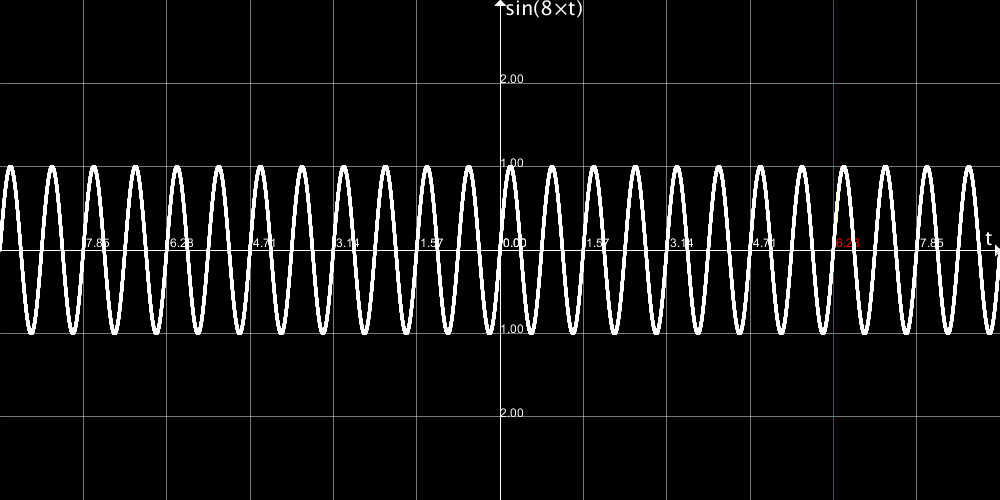
原点からの距離を角度に依存して変化させることができれば、線を曲げることができます。ここではsin()を追加しました。sin()関数は以下のようなグラフです。

図で、tとなっているところは、ここではadjustedAngleです。今回は、この三角関数を、「基準となる距離からどれだけずれているか」ということを表すのに使います。原点からの距離にこの「ずれ」を足せば、その距離を角度ごとに変えることが出来て、線を曲げることができますね？

実行結果：

あれ...変わって無くない...?

線を曲げる(リベンジ) (重要)

思い通りにならないのは、主に二つの問題によります。ひとつずつ解決しましょう。

(細かい話が苦手な人はこの段階の最後に行ってください。でもとりあえず読んでみることをお勧めします。)

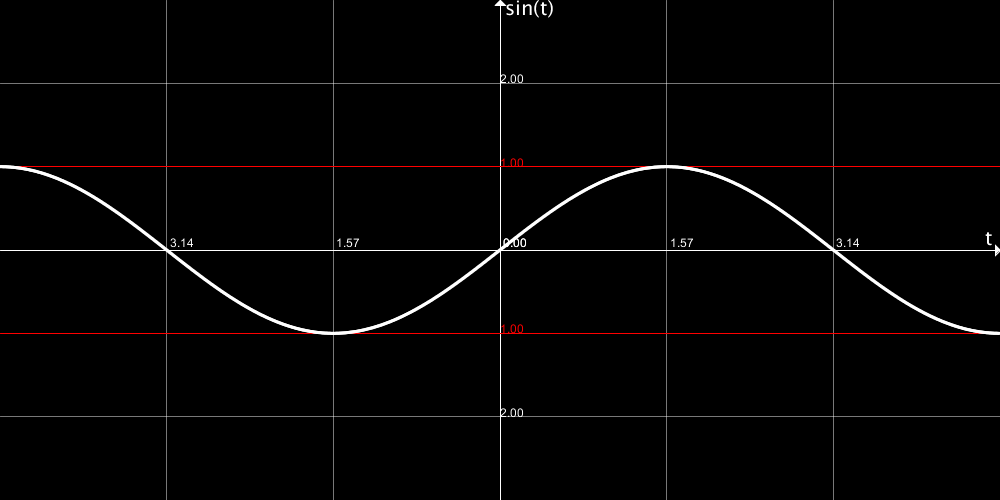
振幅(値の振れ幅の大きさ)

sin関数のグラフを再び見ましょう。

そうです。ずれはせいぜい±1の範囲でしか起きないのです。
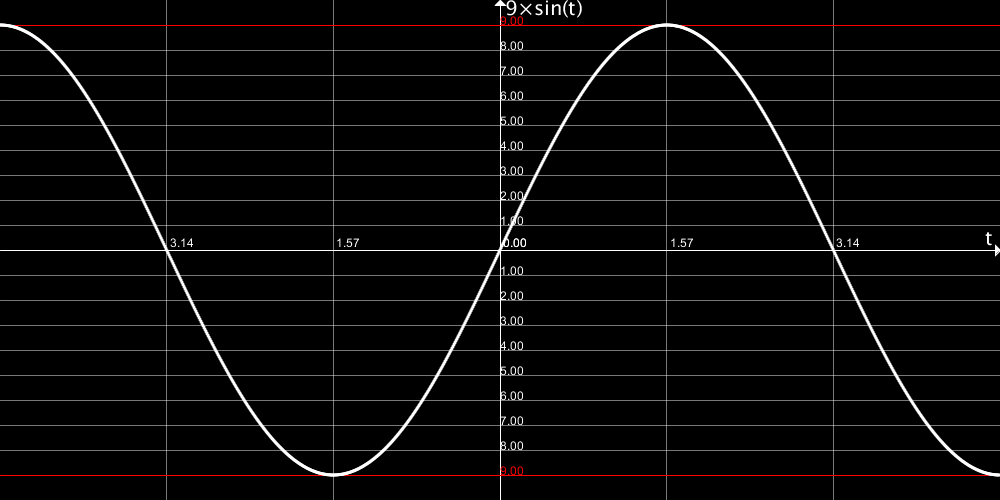
このずれを大きくするために、sin関数の結果を何倍かにする必要があります。
今回は、勘で9倍を選択しました。

float adjustedRadius = radius + sin(adjustedAngle);

を

float adjustedRadius = radius + 9 * sin(adjustedAngle);

と書き換えたら良さそうです。

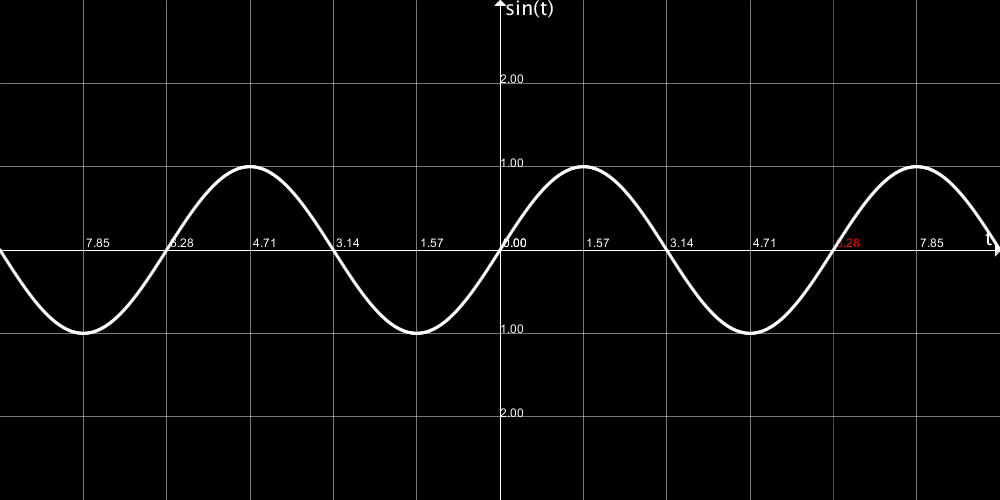
周期(値の変化の速さ)

次の問題はここにあります。

angleは、0からTAUの間でしか動きません。その間に波は、一往復分しか動かないのです。
つまり、ぐねぐねさせるにはこの範囲内(t=0～TAU)でもっとたくさん波を動かす必要があります。

そのためには、波をx方向について縮める必要があります。しかしそんなことが可能でしょうか。

結論から言うと、可能です。

sin(8 * t) とすることで、tが0からTAUまで動く間に、波は8往復するようになります。
これの理解はなかなか難しいですが、「8を掛けあわせる」というブースターのようなものを持ってグラウンドを一周する人を思い描くといいかもしれません。

float adjustedRadius = radius + sin(adjustedAngle);

を

float adjustedRadius = radius + sin(adjustedAngle * 8);

と書き換えたら良さそうです。

上記のまとめ

上二つで解説したものは、ちゃんと端から端まで理解・記憶する必要はなく、ぼんやりと「ああそういうものか」と思ってください。
では上の二つをまとめます。

void setup() {
  size(500, 500);
}

void draw() {
  clear();
  noStroke();

  //半径の変化
  for (float radius = 0; radius < 400; radius += 30) {
    //角度が0からPI*1.5の間で、半径radiusの位置に円を描く。
    for (float angle=0; angle<PI*1.5; angle += 0.01) {
      //パラメータの調整
      float adjustedAngle = angle;      
      float adjustedRadius = radius + 9 * sin(adjustedAngle * 8);
      circle(250 + adjustedRadius * cos(adjustedAngle), 250 + adjustedRadius * sin(adjustedAngle), 5);
    }
  }
}

実行結果：

成功です！
ぐにゃぐにゃ曲がりましたね。三角関数を「ずれ」として使うときは、今説明した二つの要素の調整を強くお勧めします。

でこぼこの位置をずらす

全部同じ位置が出っ張っていてもつまらないと思う(?)ので、ずれの位置を調節します。

void setup() {
  size(500, 500);
}

void draw() {
  clear();
  noStroke();

  //半径の変化
  for (float radius = 0; radius < 400; radius += 30) {
    //角度が0からPI*1.5の間で、半径radiusの位置に円を描く。
    for (float angle=0; angle<PI*1.5; angle += 0.01) {
      //パラメータの調整
      float adjustedAngle = angle;      
      //radiusをsinの引数に追加
      float adjustedRadius = radius + 9 * sin(adjustedAngle * 8 + radius);
      circle(250 + adjustedRadius * cos(adjustedAngle), 250 + adjustedRadius * sin(adjustedAngle), 5);
    }
  }
}

実行結果：

これは、三角関数の性質とかはあまり関係が無いです。
そもそも、関数とは「引数に応じて値が一つに決まる」ものでした。
よって、sin波の引数にradiusの値 を足してやると、radiusが違うとsin関数の値も違う、という様にできます。

それぐらい大雑把な物なのです。

円だったものを回す

つぎに、動きのあるスケッチにしたいのと、右上が開いていて寂しいのでこの円たちを回転させます。

void setup() {
  size(500, 500);
}
//フレーム数
float frame = 0;
void draw() {
  clear();
  noStroke();

  //半径の変化
  for (float radius = 0; radius < 400; radius += 30) {
    //角度が0からPI*1.5の間で、半径radiusの位置に円を描く。
    for (float angle=0; angle<PI*1.5; angle += 0.01) {
      //パラメータの調整
      float adjustedAngle = angle + frame / 30;      
      float adjustedRadius = radius + 9 * sin(adjustedAngle * 8 + radius);
      circle(250 + adjustedRadius * cos(adjustedAngle), 250 + adjustedRadius * sin(adjustedAngle), 5);
    }
  }

  frame++;
}

実行結果(実際は動きます)：

まず、現在のフレーム数(経過した時間)を表す変数であるframeを定義します。
frameCountという定義済みのものもありますが、自分で新しく変数を定義したほうが融通が利いて便利です。

次に、adjustedAngle に、angleにフレーム数を足したものを代入するようにします。
これによって、描画する全ての円の、中心からの角度を経過時間分だけずらすことができます。
フレーム数の変化は大きすぎるので、30ぐらいで割ってから足し合わせます。(sin波の振れ幅の調整と同じ感覚です。)

円の回転速度をずらす　(少し重要)

全部同じ回転速度だと空の空間がいつもあってやはりさみしいので、中心からの距離によって回転速度を変えることにしましょう。

void setup() {
  size(500, 500);
}
//フレーム数
float frame = 0;
void draw() {
  clear();
  noStroke();

  //半径の変化
  for (float radius = 0; radius < 400; radius += 30) {
    //角度が0からPI*1.5の間で、半径radiusの位置に円を描く。
    for (float angle=0; angle<PI*1.5; angle += 0.01) {
      //パラメータの調整
      float adjustedAngle = angle + frame / 30 * noise(radius);      
      float adjustedRadius = radius + 9 * sin(adjustedAngle * 8 + radius);
      circle(250 + adjustedRadius * cos(adjustedAngle), 250 + adjustedRadius * sin(adjustedAngle), 5);
    }
  }

  frame++;
}

実行結果(実際は動きます)：

まず、移動距離は(時間)×(速度)で求めることができました。時間がとても大きい時、速度のほんの少しの変化で大きく距離が変わってしまいます。
従って、速度は一定でないと、最終的には動きががくがくして見づらくなってしまいます。

新たに追加したnoise関数は、ここではrandomの亜種として扱っています。
noise関数もsin関数と同じく、「引数によって値がただ一つに決まる」ものです。
言い換えると、「同じ引数を与えれば同じ値が返ってくる」ということです。

これは、「時間に関わらず一定な、ある変数に応じた固定値(ただし、変数の値が少し違うなら大きく違う結果になる)」を得るのにとても役に立ちます。

ということで、noiseをフレーム数に掛けることで、radiusが同じである円は一定の速度で回り続けるようにできます。その上で、radiusが違うと大きく速度に差が開くようになっています。

開始時刻を八百長する (ラスト)

速度は変えることができましたが、開始時点では結局全部同じ場所が開いていてあまり美しくないので、バラバラの位置から開始するようにします。

void setup() {
  size(500, 500);
}
// フレーム数 ここを変更する
float frame = 9000;
void draw() {
  clear();
  noStroke();
  for (float radius = 0; radius < 400; radius += 30) {
    for (float angle = 0; angle < PI*1.5; angle += 0.01) {
      // 修正済みのパラメーター
      float adjustedAngle = angle + frame / 30 * noise(radius);
      float adjustedRadius = radius + 9 * sin(adjustedAngle * 8 + radius);
      circle(250 + adjustedRadius * cos(adjustedAngle), 250 + adjustedRadius * sin(adjustedAngle), 5);
    }
  }
  frame++;
}

実行結果(実際は動きます):

位置をずらすといっても、速度が既にバラバラなので、十分な時間がたった後なら、開いている場所もバラバラであるといえますね。
よって、スケッチを動かす前に、十分な時間を予め経過したものにします。
このためには単に経過時間を表すframeに9000を先に入れておきます。

こうすれば9000フレーム経過した地点から回転が始まるのでさすがにバラバラになっていますね。

完成です！ありがとうございました！

終わりに

最後まで追ってくれた人はありがとうございました。
そうでない人も、この記事に興味を持って下さりありがとうございます。より分かりやすく、より短くできるように頑張ります。

ぜひProcessigをすこってください。