RでのSARIMAモデルを使った実装例がWEB上にあまりなかったので投稿。
SARIMAモデル自体の説明は省きますが、心優しきかたが「TV朝日の視聴率推移をSARIMAモデルで予測してみる」にSARIMAモデルの概要とPythonでの実行例をまとめてくださっているので、モデルの概要理解がまだの人はそちらもご参照ください。
対象読者
SARIMAモデル(季節性自己回帰移動平均モデル)で何か分析したいが、Rでの実行方法がわからない人。
SARIMAモデルで実際どの程度予測できるのかに興味がある人。
データ準備
元データ:総務省統計局の家計調査(家計収支編)
時系列データ(二人以上の世帯)品目別の支出金額(2001年1月〜)を使用しました。
http://www.stat.go.jp/data/kakei/longtime/csv/h-mon-a.csv
上記の元データは形式としてはcsvだが、かなりエクセルに最適化されて作ってあるため、そのままではRで処理するのが大変。なので、Rで読み込めるようにエクセル上で加工したデータを用います。
加工データ:下記、github上に配置しています。
https://github.com/chaplin96/household_expenses
加工データをダウンロードの上、下記コマンドを実行。
# 今回使用するライブラリをインストールしておく。
install.packages("tseries")
install.packages("forecast")
install.packages("ggplot2")
install.packages("ggfortify")
library(tseries)
library(forecast)
library(ggplot2)
library(ggfortify)
# 家計支出データをデータフレーム型として読み込む
df_expenses<-read.csv("household_expenses.csv",fileEncoding = "Shift-JIS",stringsAsFactors = FALSE)
# tsオブジェクトに変換
ts_expenses<-ts(select(df_expenses,-time),start=c(2000,1),freq=12)
データ観察
# どのような品目があるかを観察
str(df_expenses)
# 実行結果
'data.frame': 217 obs. of 186 variables:
$ time : chr "2000-01-01" "2000-02-01" "2000-03-01" "2000-04-01" ...
$ 世帯数分布.抽出率調整. : int 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 ...
$ 集計世帯数 : int 7887 7942 7934 7922 7928 7917 7907 7908 7917 7937 ...
$ 世帯人員.人. : num 3.32 3.32 3.32 3.32 3.31 3.31 3.31 3.31 3.31 3.3 ...
$ X18歳未満人員.人. : num 0.74 0.75 0.75 0.75 0.75 0.74 0.74 0.74 0.74 0.73 ...
$ X65歳以上人員.人. : num 0.52 0.53 0.53 0.52 0.52 0.53 0.54 0.53 0.53 0.54 ...
$ うち無職者人員.人. : num 0.41 0.41 0.41 0.41 0.41 0.42 0.42 0.42 0.42 0.42 ...
$ 有業人員.人. : num 1.51 1.51 1.51 1.52 1.53 1.53 1.52 1.52 1.51 1.52 ...
$ 世帯主の年齢.歳. : num 52.4 52.6 52.7 52.6 52.7 52.6 52.7 52.9 52.8 53 ...
$ 持家率... : num 76 76.3 76.2 75.8 76.1 76 75.7 75.9 75.8 76.6 ...
$ 家賃.地代を支払っている世帯の割合...: num 22.1 22 22.6 22.2 22.6 22.9 23 22.4 22.6 22.8 ...
$ 消費支出 : int 309621 290663 335341 335276 308566 297648 326480 309993 296457 309193 ...
$ 食料 : int 73580 73309 79726 77344 81415 76721 83782 86988 76985 79477 ...
$ 穀類 : int 6100 6915 7496 7470 7447 7328 7794 7324 7631 8314 ...
$ 米 : int 2338 2919 3226 3346 3264 3165 3160 3164 3867 4386 ...
・・・(以下省略)
# 例として、今回は読書支出を取り上げる。
books<-ts_expenses[,"読書"]
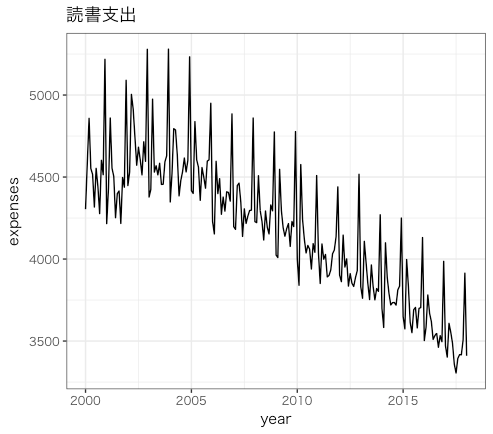
autoplot(
books,
main="読書支出",
xlab="year",
ylab="expenses"
)
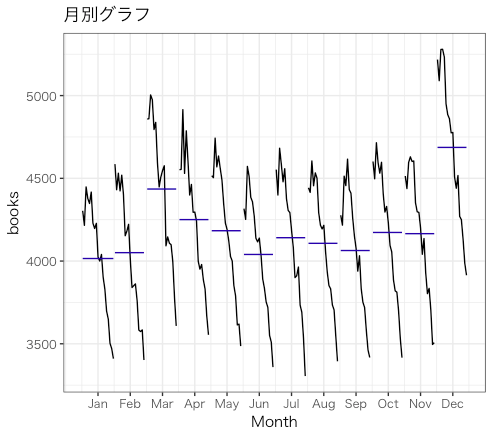
# 月別でグラフを描く
ggsubseriesplot(books)
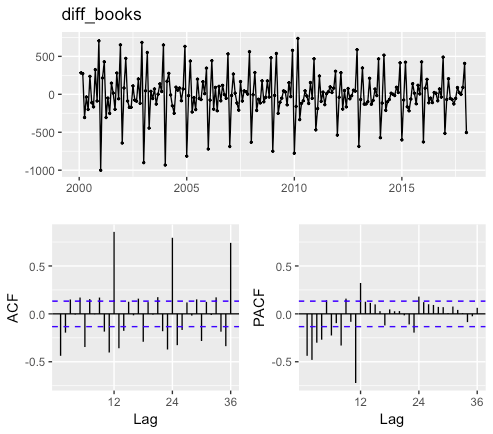
# 一階差分をとったデータのグラフを描く
diff_books<-diff(books,lag=1)
ggtsdisplay(diff_books)
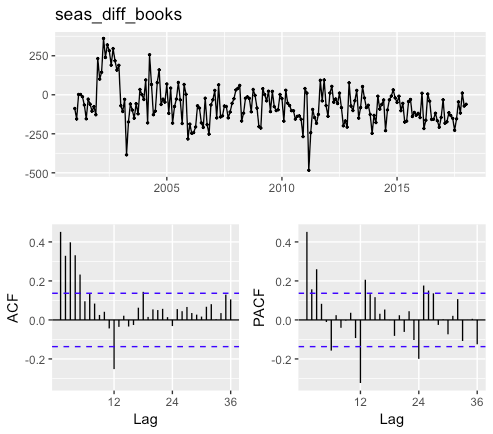
# 季節階差をとったデータのグラフを描く
seas_diff_books<-diff(books,lag=frequency(books))
ggtsdisplay(seas_diff_books)
月別グラフから読み取れること
(1)1月に最も少なく、12月に最も多くなる
(2)どの月においても、年々減少傾向である
一階差分をとったデータのグラフから読み取れること
(1)一階差分をとると定常過程になっている
(2)数期前のデータと自己相関がある
(3)12期前(1年前)のデータと強い自己相関がある
季節階差をとったデータのグラフから読み取れること
(1)1~5期前のデータと自己相関がある
(2)季節階差をとることで減少したが、相変わらず12期前(1年前)のデータと自己相関がある
(3)原系列の減少トレンドを、季節階差の定数項として表すことができそう
SARIMAモデル構築
# 学習データとテストデータに分ける
train_books<-window(books,end=c(2015,12))
test_books<-window(books,start=c(2016,1),end=c(2017,12))
# forecastパッケージに実装されているauto.arima関数を用いてSARIMAモデルを構築する。AIC(又はBIC)が最小となる次数のモデルを採用する。
m_sarima_books<-auto.arima(
y = train_books,
ic = "aic",
D = 1,
max.order = 5,
seasonal = T,
stepwise=F,
)
# auto.arima関数の引数の説明
# ic:どの情報量基準を使うかを指定(aicの他に、bicがある)
# D:何度季節階差をとるかを指定する(原系列とseas_diff_booksを見比べて、1階季節階差をとった方が、減少トレンドをうまく表現できそうだっため、今回は1を指定してみた)
# max.order:ARモデルの次数p、MAモデルの次数q、SARモデルの次数P、SMAモデルの次数Qの和の最大値を指定
# seasnal:季節性を考慮するかを指定。FALSEを指定すると、季節成分を考慮しない(P,D,Qを用いない)モデルを構築する
# stepwise:次数選択において、ステップワイズ法を使うか。falseならステップワイズを用いずに、全ての組み合わせに関して計算する
m_sarima_books
# 実行結果
Series: train_books
ARIMA(0,1,1)(2,1,1)[12]
Coefficients:
ma1 sar1 sar2 sma1
-0.6791 -0.1466 -0.1796 -0.6052
s.e. 0.0609 0.1274 0.1020 0.1210
sigma^2 estimated as 7702: log likelihood=-1058.17
AIC=2126.35 AICc=2126.69 BIC=2142.28
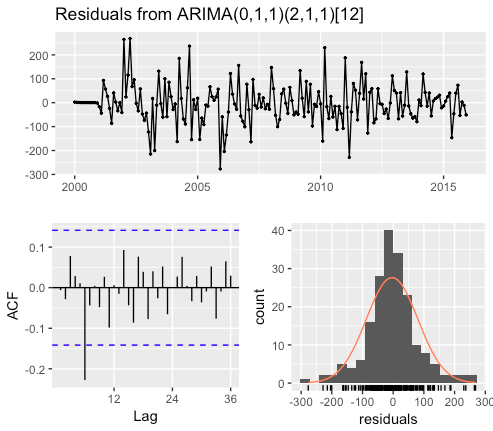
# 残差に自己相関が残っていないか、正規分布しているかをチェック
checkresiduals(m_sarima_books)
6期ほど前に自己相関が少し残っているのが気になりますが、今回は許容範囲として先に進みます。
予測
# 構築したモデルを使って、2年(24期)先まで予測してみる
f_sarima_books<-forecast(
m_sarima_books,
h=24,
level = c(95,70)
)
# levelの95,75は95%,75%予測区間も併せて出力するという指定
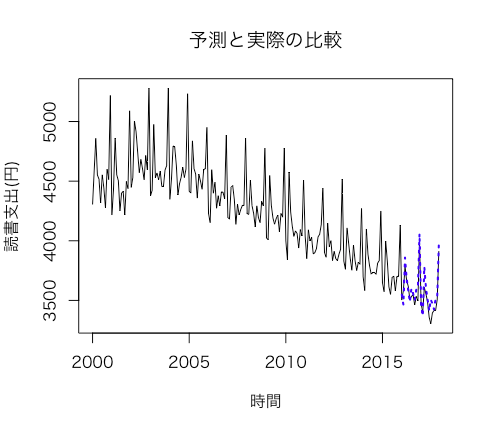
# 予測と実際の値をグラフで比較してみる。青の点線が予測値。
plot(window(books,end=c(2017,12)),xlab="時間",ylab="読書支出(円)",main="予測と実際の比較")
lines(f_sarima_books$mean,col="blue",lwd=2,lty="dotted")
ある程度うまく予測できてそうですが、次の節ではどれくらいうまく予測できたかを数値で表現します。
精度検証
# forecastパッケージのaccuracy関数を用いて予測精度を評価する
accuracy(f_sarima_books,test_books)
# 実行結果
ME RMSE MAE MPE MAPE MASE ACF1 Theil's U
Training set -3.663173 83.78706 60.08917 -0.09521795 1.394424 0.5650724 -0.005997121 NA
Test set -43.082400 78.31399 61.46071 -1.22261005 1.741044 0.5779702 -0.044425539 0.4378374
様々な指標が出てくるが、元データと単位が揃っているRMSE(平均二乗誤差平方根)が直感的にはわかりやすいと思います。
月ごとの読書支出を80円程度の誤差で予測できているので、精度は良さそうです。
しかし、今回構築したSARIMAモデルが本当に優れているのかは、他の単純なモデルと比較して初めてわかります。
例えば、今までの月平均を予測値として出力するモデルのRMSEと、SARIMAのRMSE比べてみることにしましょう。
# 月毎の平均値を算出する
f_mean<-tapply(train_books,cycle(train_books),mean)
# 2年分の予測値を時系列データオブジェクトとして作成する
f_mean_ts<-ts(rep(f_mean,2),start=c(2016,1),frequency = 12)
# 予測精度の検証
accuracy(f_mean_ts,test_books)
# 実行結果
ME RMSE MAE MPE MAPE ACF1 Theil's U
Test set -732.875 738.9992 732.875 -20.71808 20.71808 0.3346646 4.019559
単純な平均値では、RMSEは740程度なので、構築したSARIMAモデルは比較的良い精度だと言えそうです。(めでたし。)
まとめ
SARIMAモデルの構築自体は、forecastパッケージを用いれば簡単にできます。ただし、精度の良いモデルを作るには色々な角度から作図してデータの特性を理解する必要があります。
また、今回使用したデータの中には読書支出以外にも多くの支出データが含まれているので、ぜひ遊んでみてください!!
余談ですが、VAR(ベクトル自己回帰)でデータ同士の因果関係を分析してみても面白いかもしれませんね。
参考文献
馬場真哉『時系列分析と状態空間モデルの基礎 RとStanで学ぶ理論と実装』
沖本竜義『経済・ファイナンスデータの軽量時系列分析』
「[TV朝日の視聴率推移をSARIMAモデルで予測してみる]
(https://qiita.com/mshinoda88/items/749131478bfefc9bf365)」