区画モデルとは
区画モデル (Compartmental models) は感染症が人や動物、その他生物の集団の中で伝播していく力学をモデル化するために用いられる一般的な数理モデルの総称である。
区画モデルは感染症モデリングの分野で最もよく使われているが、情報の伝播をモデリングするためにも使用することができる。
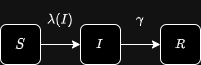
区画モデルでは、集団内の個体に対して感染状態に応じて「区画」と呼ばれるラベルを割り当てられる。例えば区画モデルの中でも最もシンプルなSIRモデルは個体を感受性保持者 (Susceptible)、感染性保持者 (Infectious)、免疫保持者 (Recovered) の3つの区画に分ける。SIRの他にSEIR、SIS、SVI等と様々なバージョンが存在する。
SIRモデル
区画モデルの概念を理解するために、ここではSIRモデルに着目する。まず表記を定義する:
- $S$: 感受性保持者 (まだ感染したことがなくこれから感染し得る人) の人口 (単位: 人)
- $I$: 感染性保持者 (感染している人) の人口 (単位: 人)
- $R$: 免疫保持者 (感染した後に回復した人) の人口 (単位: 人)
仮定
モデルを簡略化させるために次の仮定をおく。まず、感染性保持者は一定の率 $\gamma$ で回復する=免疫保持者になる。また一般的にはある個体が感染してから他の固定を感染させる程の感染力を獲得するまで、しばらく時間を要するが、一旦時間のラグがないとする。さらに、人口動態、すなわち自然出生率と死亡率は無視する。
感染力 Force of infection
伝播プロセスへの理解を深めるため、各区画に所属する人口の変化を表現する常微分方程式系 (System of ordinary differential equations (ODEs)) を考える。感染性保持者が一人あたり感染させる感受性個体の割合は感染力 (force of infection) と呼ばれここでは $\lambda(I)$ と表記する。留意すべき点として、$\lambda(I)$ は定数ではなく感染性保持者の人口 $I$ の関数である。
$\lambda(I)$ は個人間の接触の性質に関する仮定に依存するため定義が厄介になることが多い。しかし、ここでは難しく考えすぎず、感染力を感染率 $\beta$ と感染性保持者の積としてモデリングできるとする。$N = S + I + R$ を総人口とすると、感染力は
$$
\lambda(I) = \beta \frac{I}{N}
$$
と書ける。するとSIRモデルの微分方程式系は次のように書くことができる:
$$
\frac{dS}{dt} = -\lambda(I)S, \quad \frac{dI}{dt} = \lambda(I)S - \gamma I, \quad \frac{dR}{dt} = \gamma I.
$$
着目すべき点として、我々は今人口が「閉じている」、すなわち総人口 ($N=S+I+R$) は時間と共に変化しない ($dN_dt = 0$) と仮定していることである。このように仮定する利点は、系が三つの方程式ではなく二つの方程式で決定されることである。例えば免疫保持者の人口は $R = N - S - I$ であるため、感受性保持者人口と感染性保持者人口を求めればよい。
次回は人口動態も考慮し、SIRモデルの解析について学んでいく。
参考文献
- Julie C. Blackwood & Lauren M. Childs (2018) An introduction to compartmental modeling for the budding infectious disease modeler, Letters in Biomathematics, 5:1, 195-221, DOI: 10.1080/23737867.2018.1509026