【python】二次元系 点図形内外問題

考え方はこちらをクリック

環境

python3.7

問題

以下のような図の点Pが図形の中か外かを計算する。

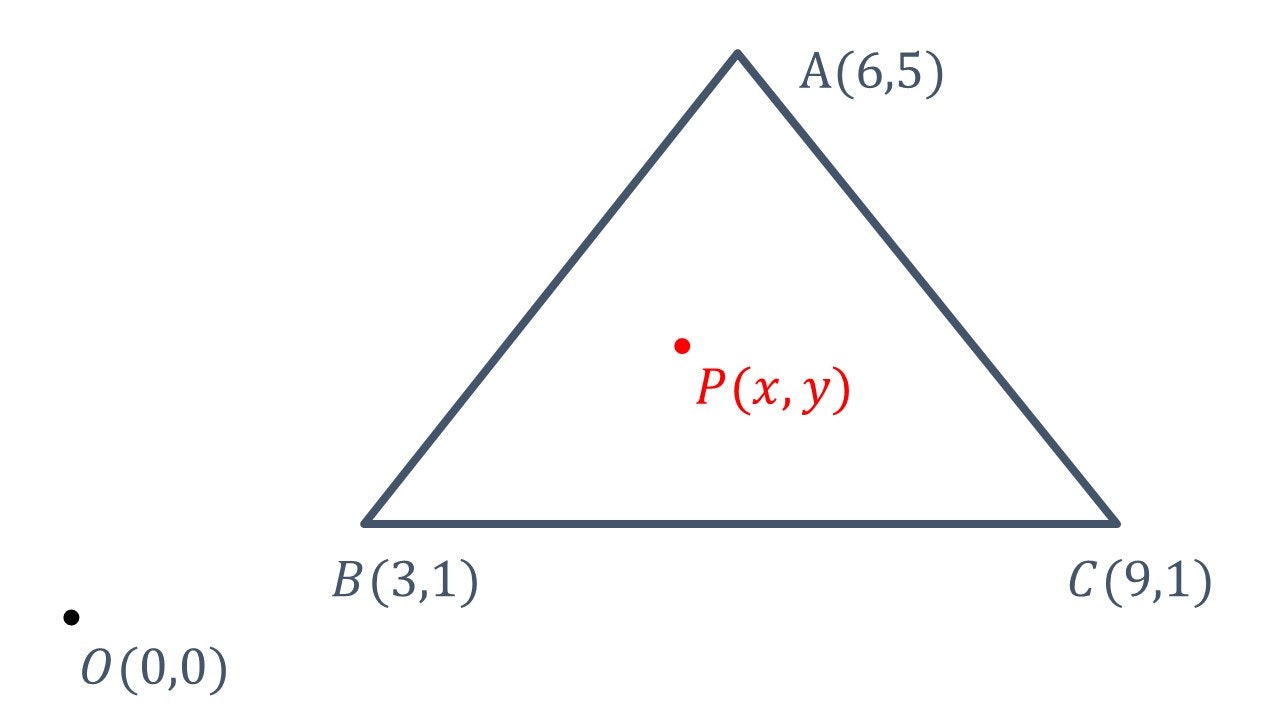
O(0,0)は原点を表している。また、A(2,2)、B(3,1)、C(3,3)は図形の頂点を表している。P(x,y)は任意の点である。

計算

下図のように外積の向きが同じになるように計算する。

座標の定義↓

import numpy 

#点Aの座標
A = numpy.array((6, 5))
#点Bの座標
B = numpy.array((3, 1))
#点Cの座標
C = numpy.array((9, 1))

外積計算↓

#点Pが図形の中にあるかどうか
def p(x, y):
    #点Pの座標
    P = numpy.array((x, y))

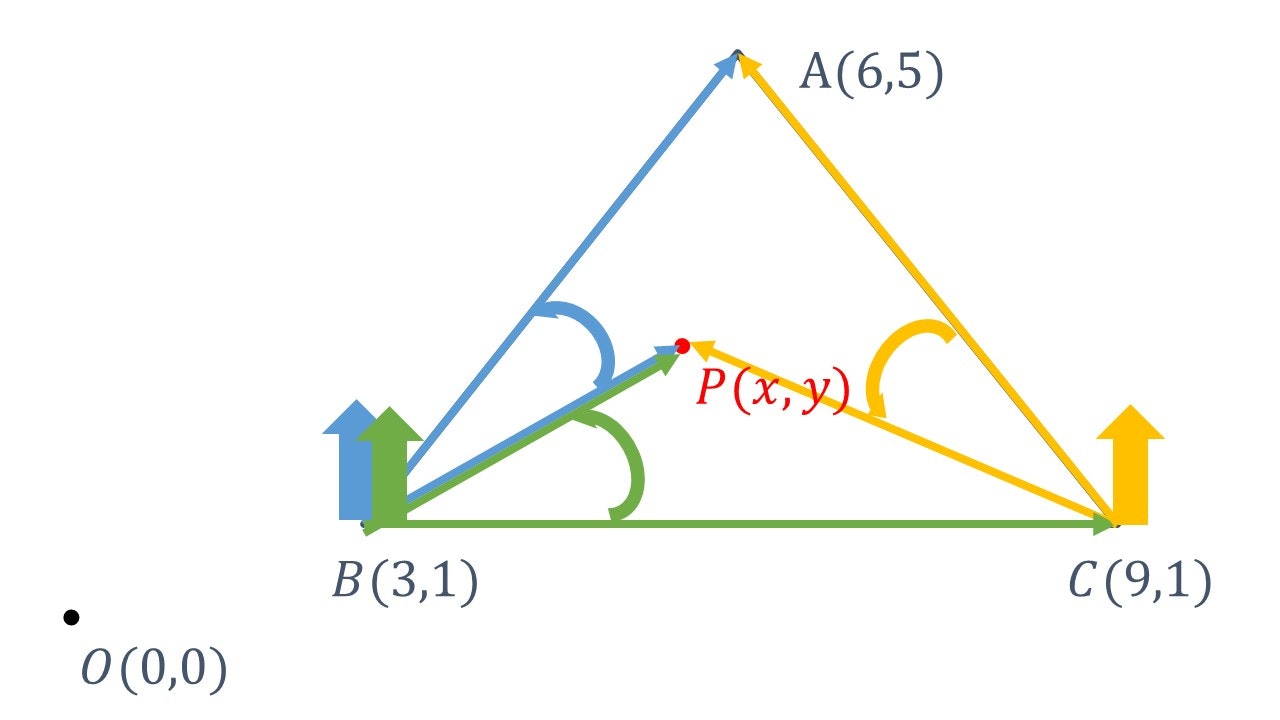
    #ベクトルBPとベクトルBAの外積
    abp = numpy.outer(P-B, A-B)
    #ベクトルBCとベクトルBPの外積
    pbc = numpy.outer(C-B, P-B)
    #ベクトルCAとベクトルCPの外積
    apc = numpy.outer(A-C, P-C)

    #ベクトルBPとベクトルBAの外積の行列式
    abp = numpy.linalg.det(abp)
    #ベクトルBCとベクトルBPの外積の行列式
    pbc = numpy.linalg.det(pbc)
    #ベクトルCAとベクトルCPの外積の行列式
    apc = numpy.linalg.det(apc)

    #ベクトルBPとベクトルBAの外積の行列式が他の行列式の符号と一致したら、Trueを返す
    if numpy.sign(abp)==numpy.sign(pbc) and numpy.sign(abp)==numpy.sign(pbc):
        return True
    #ベクトルBPとベクトルBAの外積の行列式が他の行列式の符号と一致しなかったら、Falseを返す
    else:
        return False 

すべてのコードと結果

コード

code.py

import numpy 

#点Aの座標
A = numpy.array((6, 5))
#点Bの座標
B = numpy.array((3, 1))
#点Cの座標
C = numpy.array((9, 1))


#点Pが図形の中にあるかどうか
def p(x, y):
    #点Pの座標
    P = numpy.array((x, y))

    #ベクトルBPとベクトルBAの外積
    abp = numpy.outer(P-B, A-B)
    #ベクトルBCとベクトルBPの外積
    pbc = numpy.outer(C-B, P-B)
    #ベクトルCAとベクトルCPの外積
    apc = numpy.outer(A-C, P-C)

    #ベクトルBPとベクトルBAの外積の行列式
    abp = numpy.linalg.det(abp)
    #ベクトルBCとベクトルBPの外積の行列式
    pbc = numpy.linalg.det(pbc)
    #ベクトルCAとベクトルCPの外積の行列式
    apc = numpy.linalg.det(apc)

    #ベクトルBPとベクトルBAの外積の行列式が他の行列式の符号と一致したら、Trueを返す
    if numpy.sign(abp)==numpy.sign(pbc) and numpy.sign(abp)==numpy.sign(pbc):
        return True
    #ベクトルBPとベクトルBAの外積の行列式が他の行列式の符号と一致しなかったら、Falseを返す
    else:
        return False 


print(p(3, 1))#出力結果:True
print(p(2, 2))#出力結果:True
print(p(8,14))#出力結果:False

補足
点Pを線上にあるとした時、点Pは図形の中にあるものとして計算している。