図形の中に点があるかどうかの判断のやり方。
前提条件
以下のように図形の中にあるかどうか判断したい点__P(x,y)__を図形の中にあるものとした時の図形を考える。
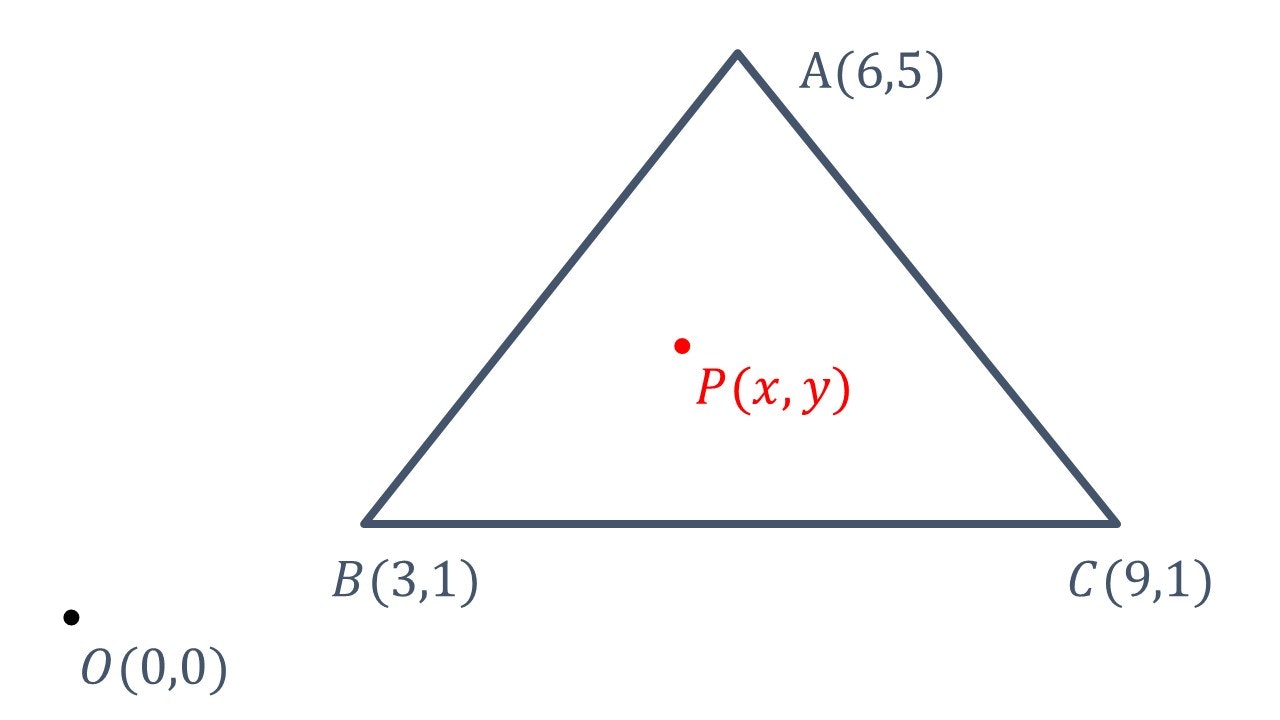
__O(0,0)__は__原点__を表している。また、__A(2,2)、B(3,1)、C(3,3)は図形の__頂点__を表している。P(x,y)__は__任意の点__である。
図形の内外判定→外積を使う
__P(x,y)__が__三角形ABC__の中にあるかどうかを外積を使って考える。
以下の図のような図を考える。
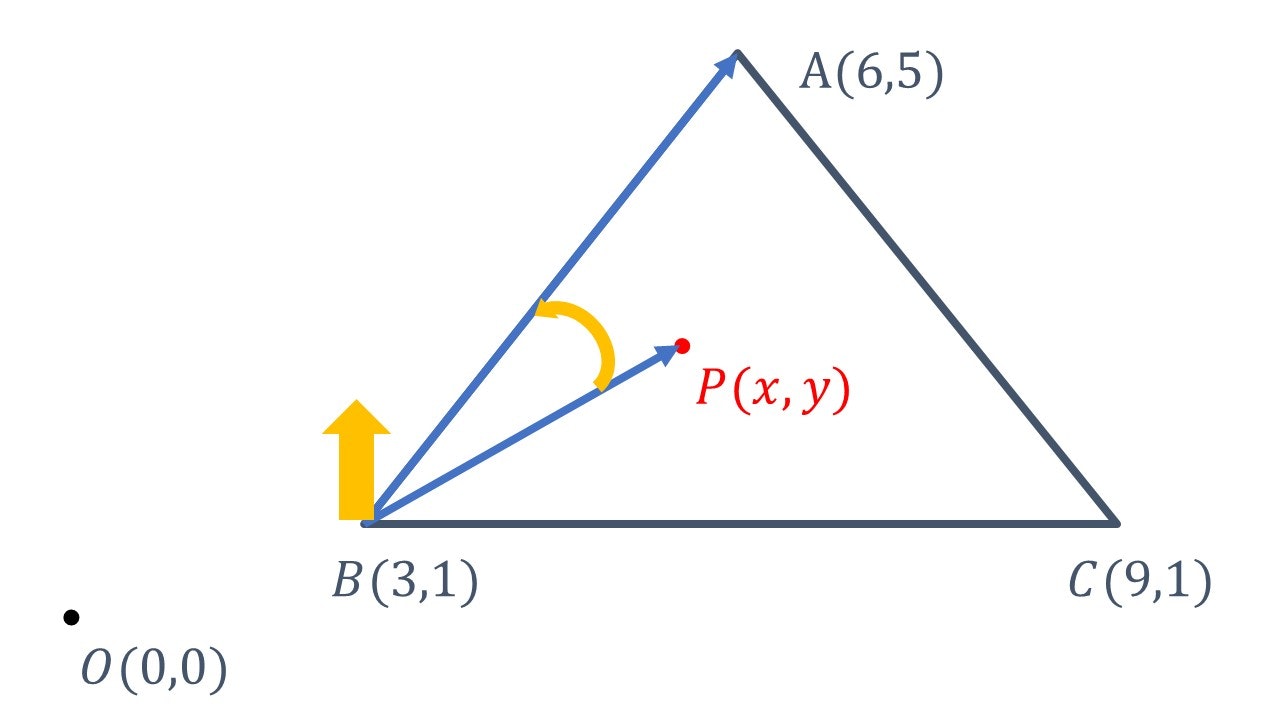
この図は$\vec{BP}$と$\vec{BA}$の外積を表している。
これを以下の図のように__外積の矢印が同じ向き__になるように三角形PBC、三角形PCAでも同様にして外積を計算する。
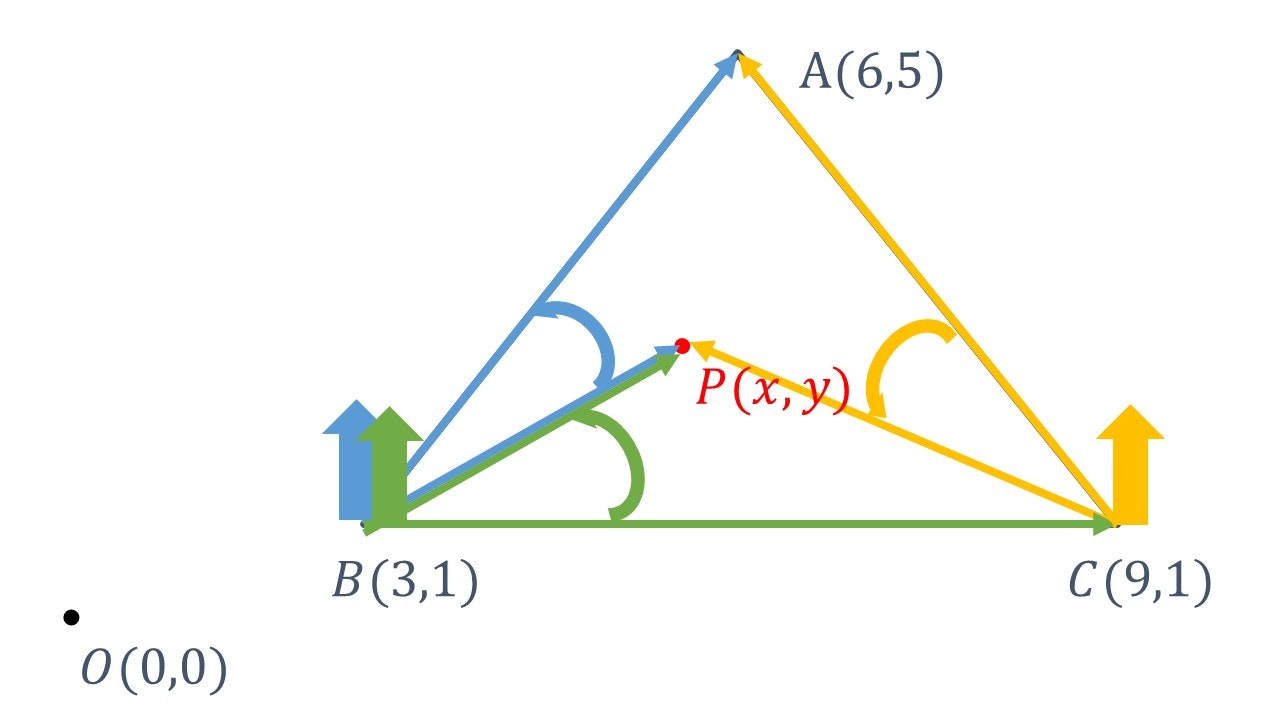
上図は$\vec{BP}$と$\vec{BA}$の外積、$\vec{BC}$と$\vec{BP}$の外積、$\vec{CA}$と$\vec{CP}$の外積を表している。
計算結果
以上のように計算した__外積がすべて同じ向き(符号)__なら、図形の中にあるかどうか判断したい点__P(x,y)__は図形の中にある。
もしそうでない場合は点__P(x,y)__は図形の外側にある。
点が図形の外側の時
もし計算した外積が__同じ向き(符号)でない__ときは、図形は以下のようになっている。
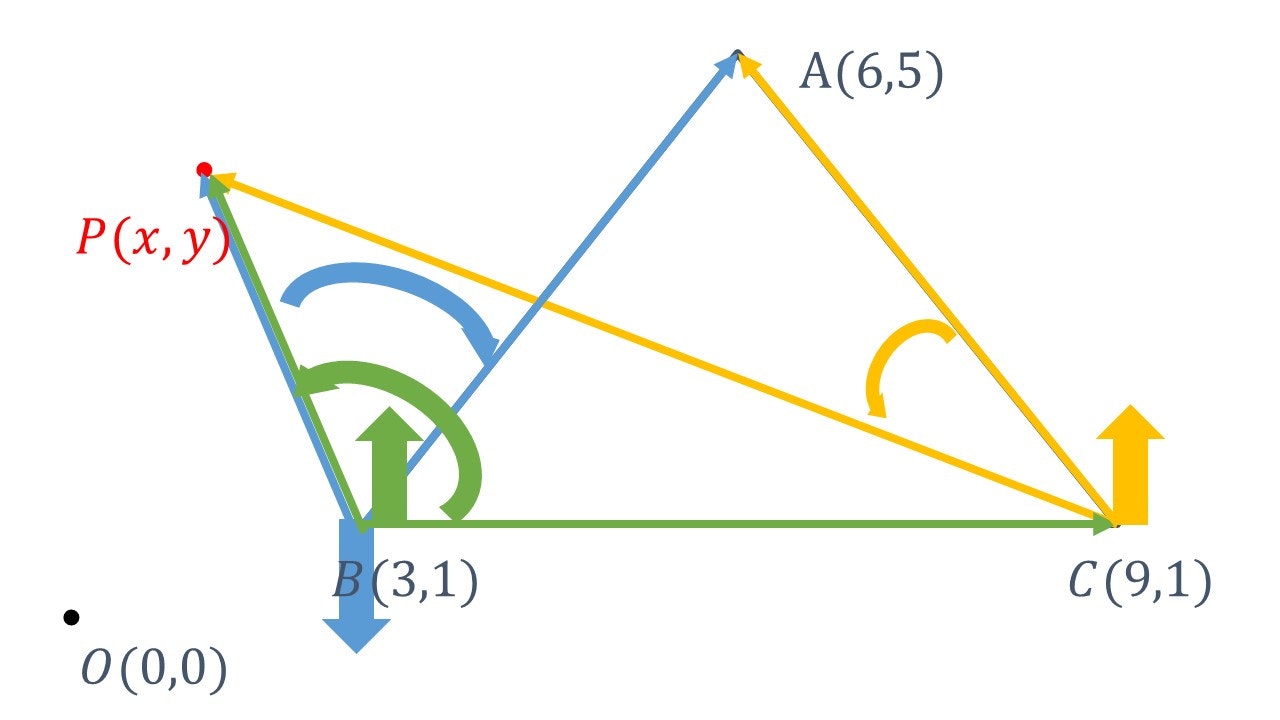
これは、$\vec{BP}$と$\vec{BA}$の外積だけ、$\vec{BC}$と$\vec{BP}$の外積、$\vec{CA}$と$\vec{CP}$の外積とは__違う向き(符号)__を表している。
このように点が図形の外側にあると外積の向き(符号)がすべて揃わない。