始めに
Schrödingerの猫[1]とは,諸々の実験装置と一緒に箱の中に閉じ込められた可哀そうな猫のことで,次に箱を開けてみるまで,その猫は「生きている」と「死んでいる」の重ね合わせの状態にあります.
さて,Spectral Bias[2]は深層学習分野において大きな問題ですが,この子もブラックボックスという箱に閉じ込められた存在で,箱を開けてみるまでは「存在する」と「存在しない」が重ね合わせてあります.恐れずに箱を開けましょう.つまり,本稿ではSpectral Biasを観測してみます(コードはGitHubに公開しています).
Spectral Bias
深層学習におけるSpectral Biasとは,低周波成分の学習が,高周波数の成分より優先される現象を指します.任意の関数が表現可能であり,既に広い適用例を持っているニューラルネットワークですが,この現象は様々な問題で指摘されています[2, 3].
例えば,Rahaman et al.[2]は以下のように記しています:
While they (neural networks) can approximate arbitrary functions, we find that these networks prioritize learning the low frequency modes, a phenomenon we call the spectral bias. This bias manifests itself not just in the process of learning, but also in the parameterization of the model itself: in fact, we show that the lower frequency components of trained networks are more robust to random parameter perturbations.
これを研究すれば,オーバーパラメトライズされたニューラルネットワークが様々なタスクで成功してきた背景を知ることができるかもしれません.あるいは,これを取り除くことができれば,学習の高速化や推論の汎化に繋がる鍵が見つかるかもしれませんね.
数値実験
それでは,実験を通して観測してみましょう.
以下の実験では,関数は時間の関数($f = f(t)$)としています.ただし,上述の通り,Spectral Biasは周波数に関する話題なので,時間領域ではなく周波数領域で議論したい気持ちです.時間領域のシグナルを周波数領域へマッピングするにはFourier変換が良いでしょう.
時間領域の関数$f(t)$に対するフーリエ変換を$\hat{f}(\omega)=\mathcal{F}\left[ f(t) \right]$と書くこととします.このとき,逆変換は$f(t)=\mathcal{F}^{-1}\left[ \hat{f}(\omega) \right]$と書けます.それぞれの定義式は以下の通りです.
\begin{align}
\hat{f}(\omega)&=\frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} f(t) e^{-i \omega t} dt \\
f(t)&=\frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} \hat{f}(\omega) e^{i \omega t} d\omega
\end{align}
ここで,$t$が時間の次元を持つとすると,$\omega$は周波数の次元を持ちます.実験では主にフーリエ変換を用い,ニューラルネットワークが返す関数の周波数成分を,本来の関数の周波数と比較してみます.
例題1
始めの例題は,以下の関数のフィッティングとします.
f(t) = 0.5 \sin(2 \pi \omega_1 t) + 0.5 \sin(2 \pi \omega_2 t) + 0.5 \cos(2 \pi \omega_3 t), t \in [0, 1]
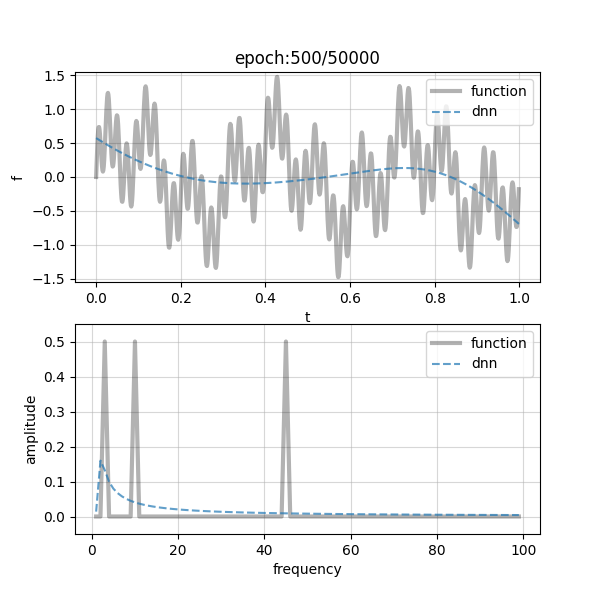
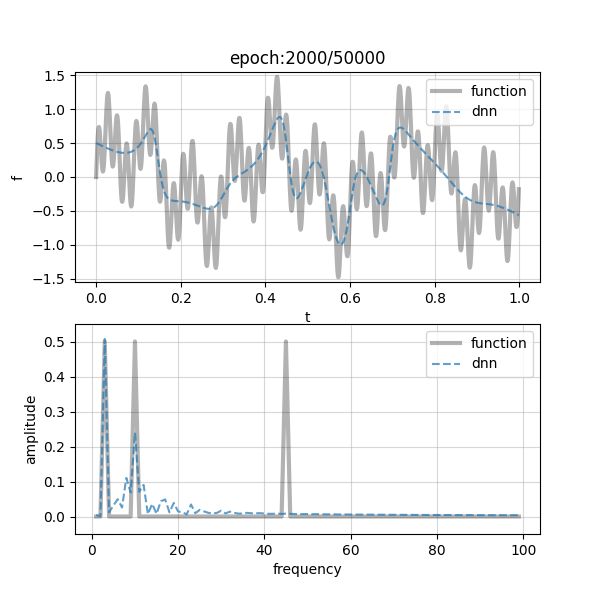
各項の周波数はそれぞれ,$\omega_1=3, \omega_2=10, \omega_3=45$としました.また,学習に用いたDNNは,width=30, depth=5の全結合ニューラルネットワークです.早速ですが,結果を以下に示します.
| epoch (progress) | epoch (progress) | epoch (progress) |
|---|---|---|
| 500 / 50,000 (1%) | 2,000 / 50,000 (4%) | 45,000 / 50,000 (90%) |
 |
 |
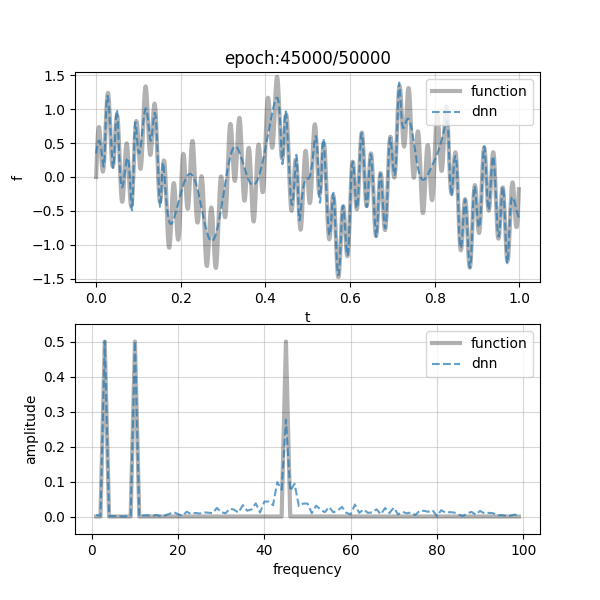 |
少し小さいかもしれませんが,クリックするとズームして確認できると思います.各図において,上部には,学習する関数$f(x)$をグレーの実線で,DNNの近似曲線を青の破線で示しています.また,下部に示しているのは,それぞれの周波数成分と振幅の関係です.図上部から,大まかな曲線の様子を学習するところから始めて,少しずつファインチューニングに移っていそうな感じがしますね!これは図下部の周波数領域のプロットを見れば一目瞭然で,左側(低周波域)から右側(高周波域)に向けてフィッティングが徐々に遷移している様子が確認できます.
例題2
続いて,以下の関数でも実験してみましょう.
f(t) = \frac{4}{\pi} \sum_{n=1}^{N} \frac{1}{n} \sin(n t), n=1,3,5,\cdots , t \in [0, 1]
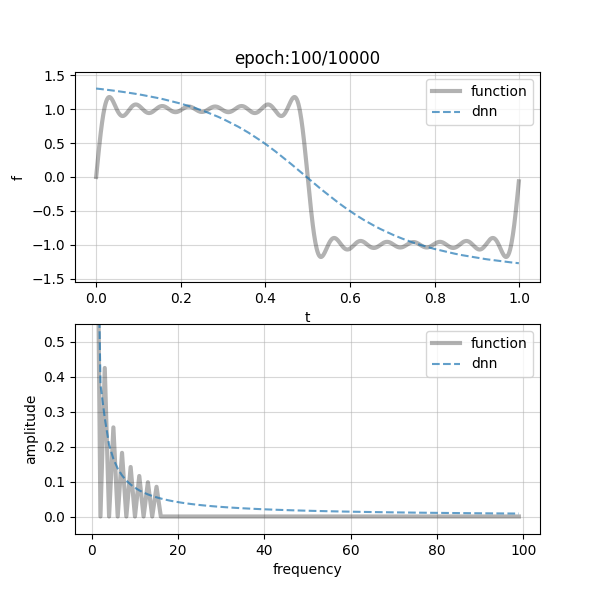
上式は正方波形の(有限な)フーリエ級数ですね,今回は$N=15$としました.DNNの構造はwidth=10, depth=5です.では,結果を示します.
| epoch (progress) | epoch (progress) | epoch (progress) |
|---|---|---|
| 100 / 10,000 (1%) | 500 / 10,000 (5%) | 9,500 / 10,000 (95%) |
 |
 |
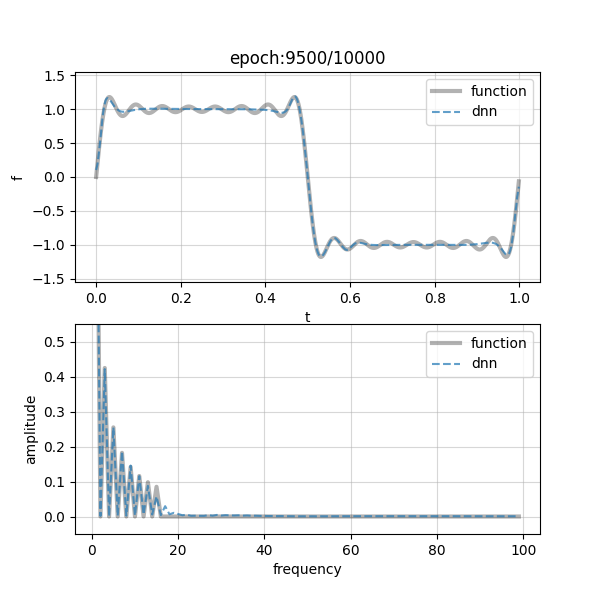 |
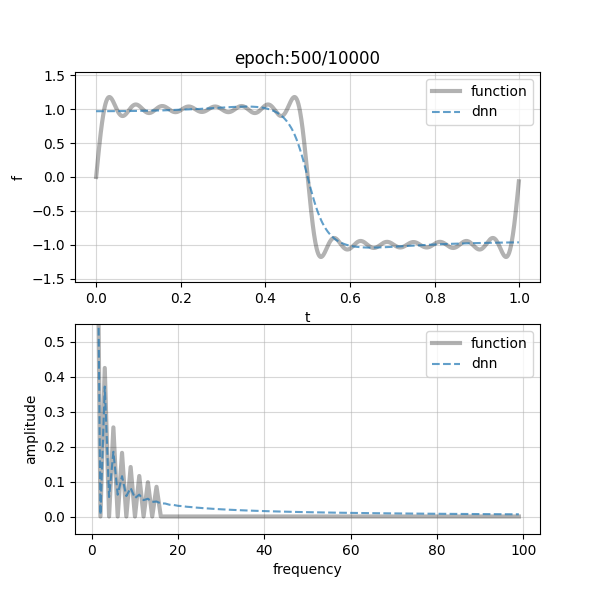
図は先ほどと同様で,上部が学習すべき関数とDNN推論値をプロットしたもので,下部が周波数空間です(グレー実線:$f(t)$,青破線:DNN).やはり左側にプロットされる低周波数成分から学習が進み,高周波へシフトしていく様子が見られます.何だか存在しない高周波成分(17~)が生まれてしまっていますが,これは本当に細かいギザギザがフィッティングできていないせいですね.
各エポック時のフィッティングの様子はGitHubのレポジトリではgifにしていますので,過程を動画っぽく見たい方はどうぞ!
終わりに
以上の2つの例題ではSpectral Biasが認められましたが,その他の問題ではまだ重ね合わせの状態にあり,観測するまで何が起きるか分かりません.皆さん,安心して学習していきましょう!
(Spectral Biasは,ほぼ全てのニューラルネットワークが抱える問題です[2, 3].こんな記事に踊らされないように気を付けましょう.)
参考文献
[1] Schrödinger, E.: Die gegenwärtige Situation in der Quantenmechanik, Naturwissenschaften, Vol. 23, pp. 807–812, 1935 (paper).
[2] Rahaman, N., Baratin, ., Arpit, ., Draxler, F., Lin, M., Hamprecht, F., Bengio, Y., Courville, A.: On the Spectral Bias of Neural Networks, International Conference on Machine Learning, 2019 (paper).
[3] Cao, Y., Fang, Z., Wu, Y., Zhou, D.X., Gu, Q.: Towards Understanding the Spectral Bias of Deep Learning, arXiv: 1912.01198, 2019 (paper).