初めに
陽的な時間積分法を学ぶ.陰解法は議論の対象から省く.特に,Runge-Kutta族とかRunge-Kutta系などと呼ばれるもの(multi-stage methods)に的を絞る.Adams系の線形多段法(linear multi-step methods),Taylor法などの高次導関数を使う方法(Taylor series methods)とは切り分ける.
思い返すと,学士課程2年次に受けたODEの講義(7年前!)で初めてRunge-Kutta法を学んだが,Butcher tableauと呼ばれるものから辞書引きのような形で係数を取り出して手計算していた.きちんと精度良く計算できるので楽しくはあったのだが,もう少し整理しながら勉強し直そう.
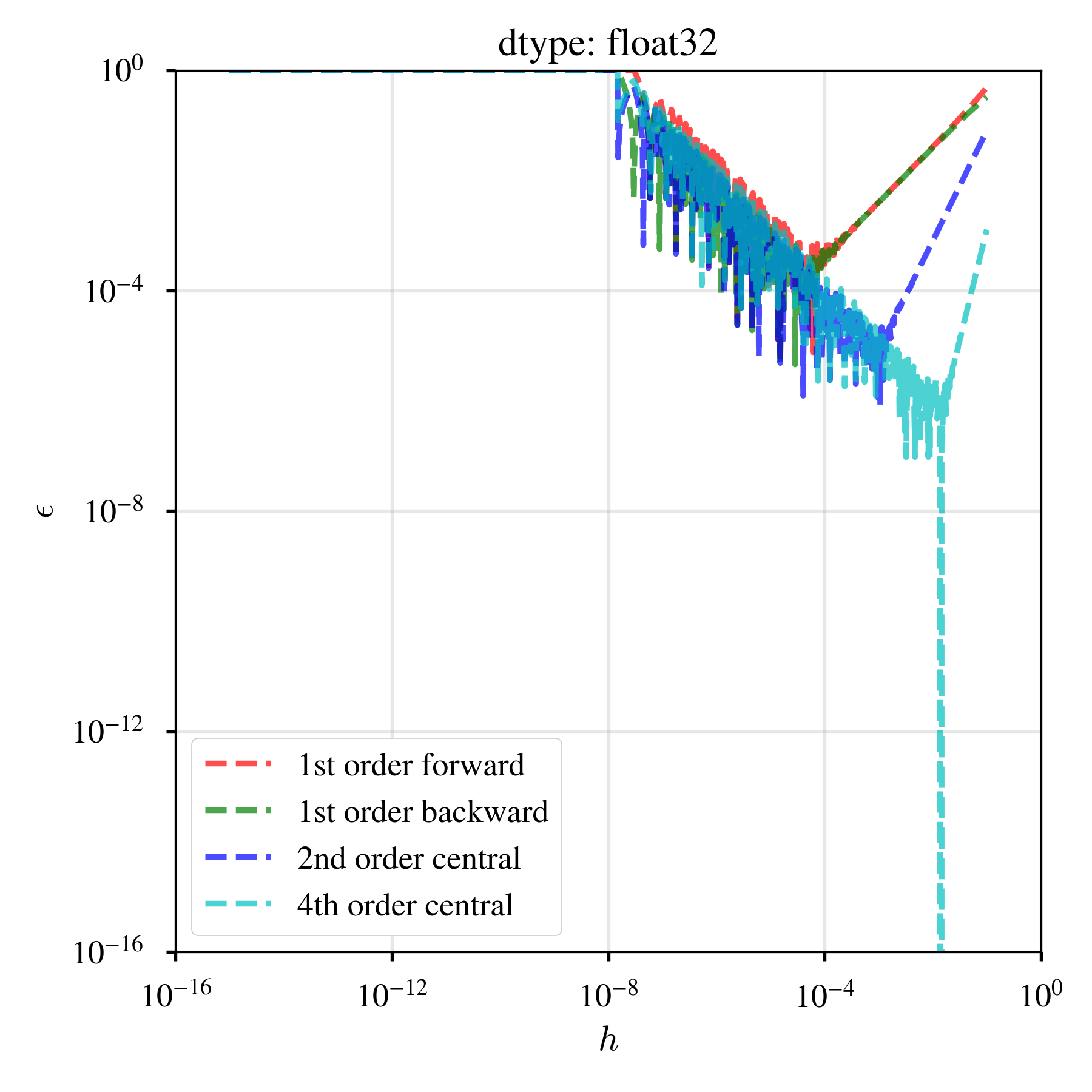
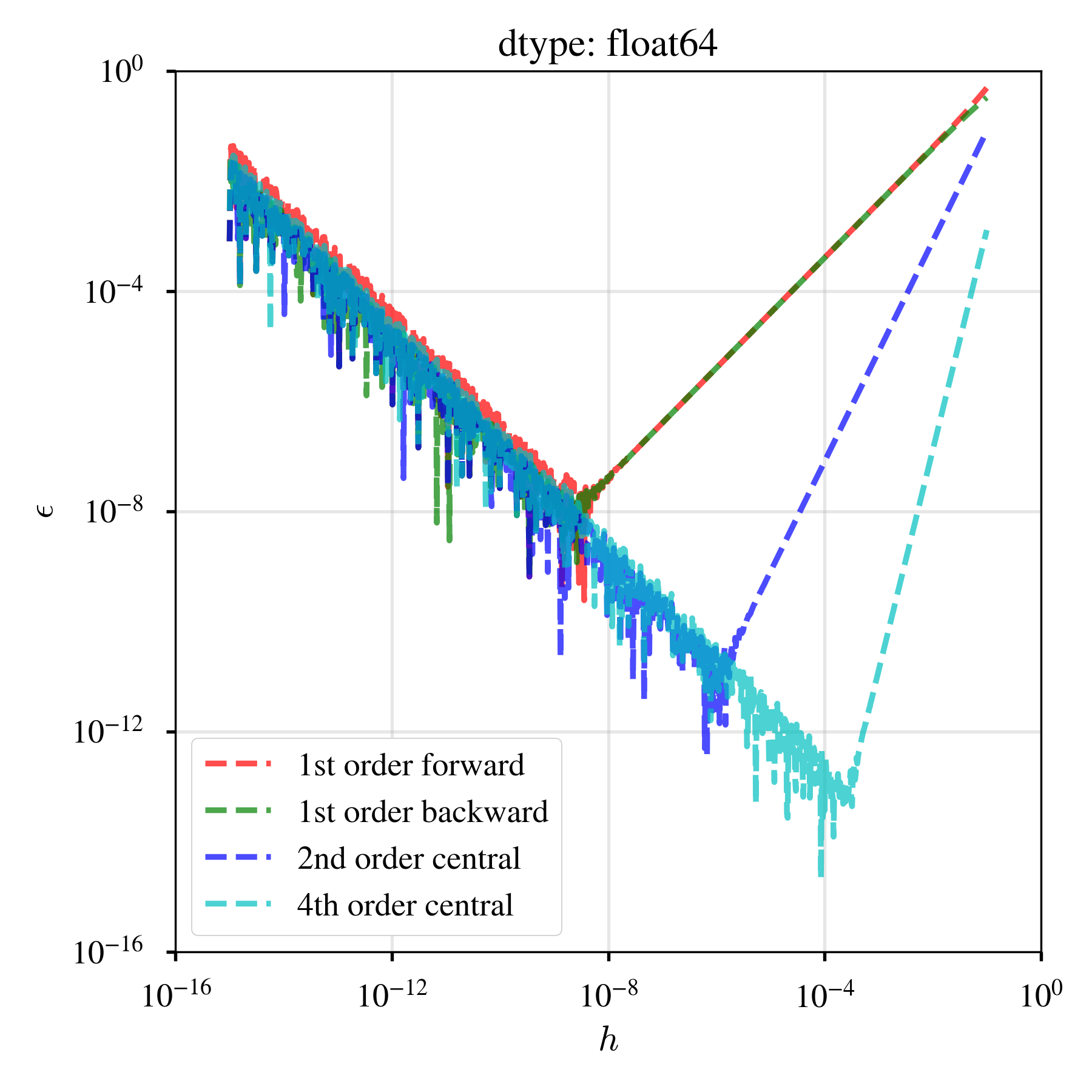
高次精度の方法を用意するマインドセットとして,$f(x) = x^5$の,$x = 0.5$での1階の導関数を,1次精度前進差分,1次精度後退差分,2次精度中心差分,4次精度中心差分の4つで近似すると,離散化パラメータ$h$と相対誤差$\epsilon$の関係は以下のようになる.
| 単精度 | 倍精度 | 四倍精度 |
|---|---|---|
 |
 |
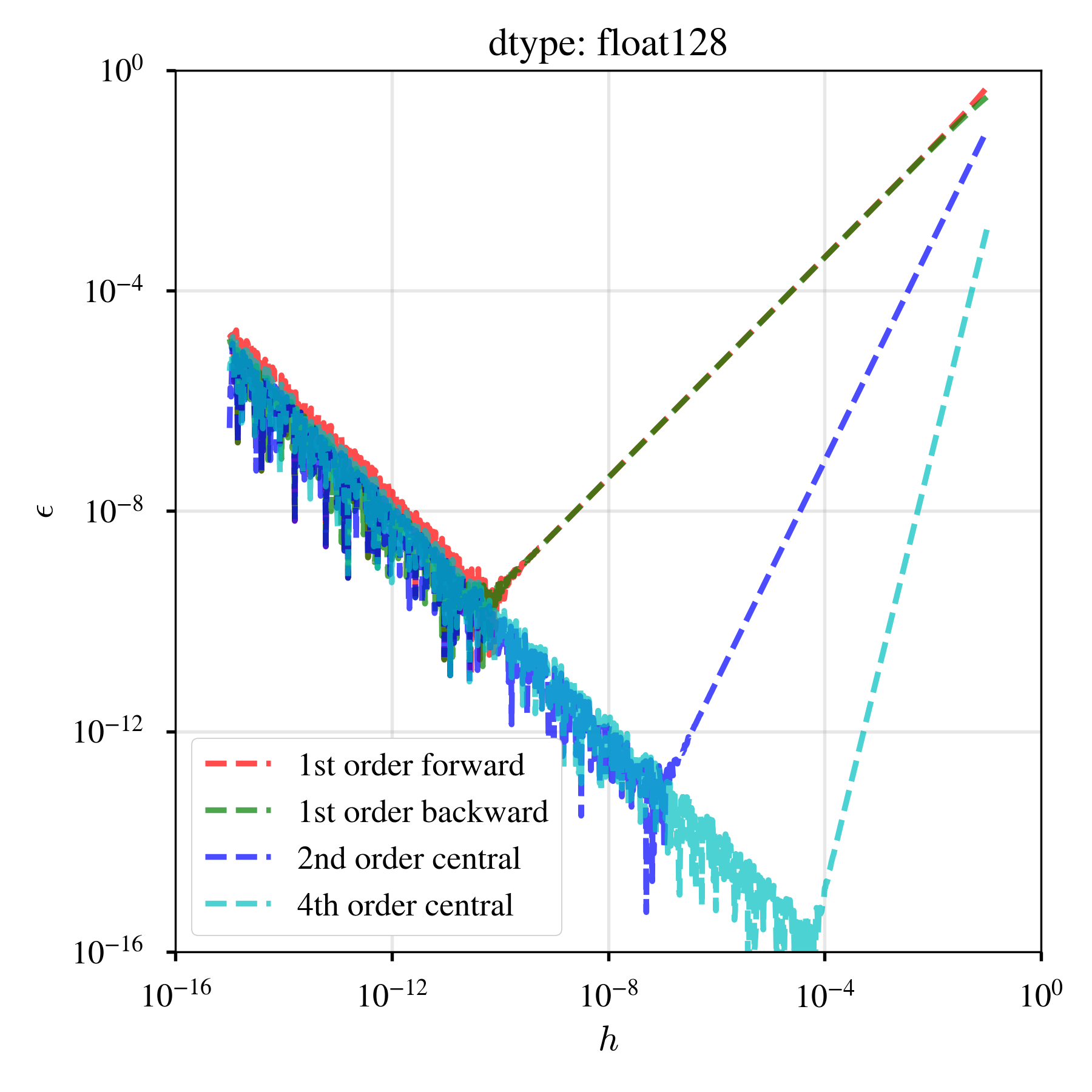 |
図より,$h$を小さくすると打切り誤差が小さくなっていくが,その後丸め誤差が卓越する(Farlow2012やBaydin+2018に同じ図がある).精度の良い方法を用意しておくと,少しの計算負荷で幾許かのpay-offが期待できる.なお,単精度・倍精度・四倍精度の浮動小数点数を使った結果を図示したが,これは個人的に違いを見てみたかっただけで,これ以降の議論は全て倍精度である.
以下が勉強になる:
- 教科書
- Hairer+1993: Solving Ordinary Differential Equations I - Nonstiff Problems
- Hairer&Wanner1996: Solving Ordinary Differential Equations II - Stiff and Differential-Algebraic Problems
- Butcher20161: Numerical Methods for Ordinary Differential Equations
- オンラインリソース
Methods
常微分方程式の初期値問題
初期値問題を考える.
\begin{align}
\frac{d}{d t} u \left( t \right)
&= f \left( t, u \left( t \right) \right) \\
u \left( 0 \right)
&= u_0 \\
\end{align}
ここで,$f: \mathbb{R} \times \mathbb{R}^{N} \to \mathbb{R}^{N}, \ u: \mathbb{R} \to \mathbb{R}^{N}, \ t \in [0, T]$である.$u = u \left( t \right)$の追跡が興味の対象である2.
Euler法
素朴に
\begin{align}
\frac{u^{(n+1)} - u^{(n)}}{\tau}
&= f \left( t^{(n)}, u^{(n)} \right) \\
u^{(n+1)}
&= u^{(n)} + \tau f \left( t^{(n)}, u^{(n)} \right) \\
\end{align}
本来,陰的Euler法との区別を明確化すべきだが,本稿のスコープは陽的な方法なので,本稿では陽的Euler法のことを単にEuler法と呼ぶことにする.
以降の議論と足並みを揃えるために,上式を次のように書き改めておく.
\begin{align}
f_{1}
&= f \left( t^{(n)}, u^{(n)} \right) \\
u^{(n+1)}
&= u^{(n)} + \tau f_{1} \\
\end{align}
何次精度か?
Euler法は何次精度か?以下のシンプルな問題を考えてみる.
\begin{align}
\frac{d}{d t} u \left( t \right)
&= \frac{u + t}{u - t} \\
u \left( 0 \right)
&= 1 \\
\end{align}
解は,$u (t) = t + \sqrt{1 + 2 t^2}$.
Taylor級数展開の剰余項も残して陽的Euler法を再掲すると,
\begin{align}
\frac{u^{(n+1)} - u^{(n)}}{\tau}
&= f \left( t^{(n)}, u^{(n)} \right)
+ \mathcal{O} \left( \tau \right) \\
u^{(n+1)}
&= u^{(n)} + \tau f \left( t^{(n)}, u^{(n)} \right)
+ \mathcal{O} \left( \tau^2 \right) \\
\end{align}
より,1ステップ当たりの打ち切り誤差は2次精度となる(局所的に2次精度).区間$[0, T]$を刻み幅$\tau$で離散化すると,$t = T$に到達するまでに$N = T/\tau$ステップだけの計算を要する.
\begin{align}
u^{(1)}
&= u^{(0)} + \tau f \left( t^{(0)}, u^{(0)} \right)
+ \mathcal{O} \left( \tau^2 \right) \\
u^{(2)}
&= u^{(1)} + \tau f \left( t^{(1)}, u^{(1)} \right)
+ 2 \mathcal{O} \left( \tau^2 \right) \\
\vdots \\
u^{(N)}
&= u^{(N-1)} + \tau f \left( t^{(N-1)}, u^{(N-1)} \right)
+ N \mathcal{O} \left( \tau^2 \right) \\
\end{align}
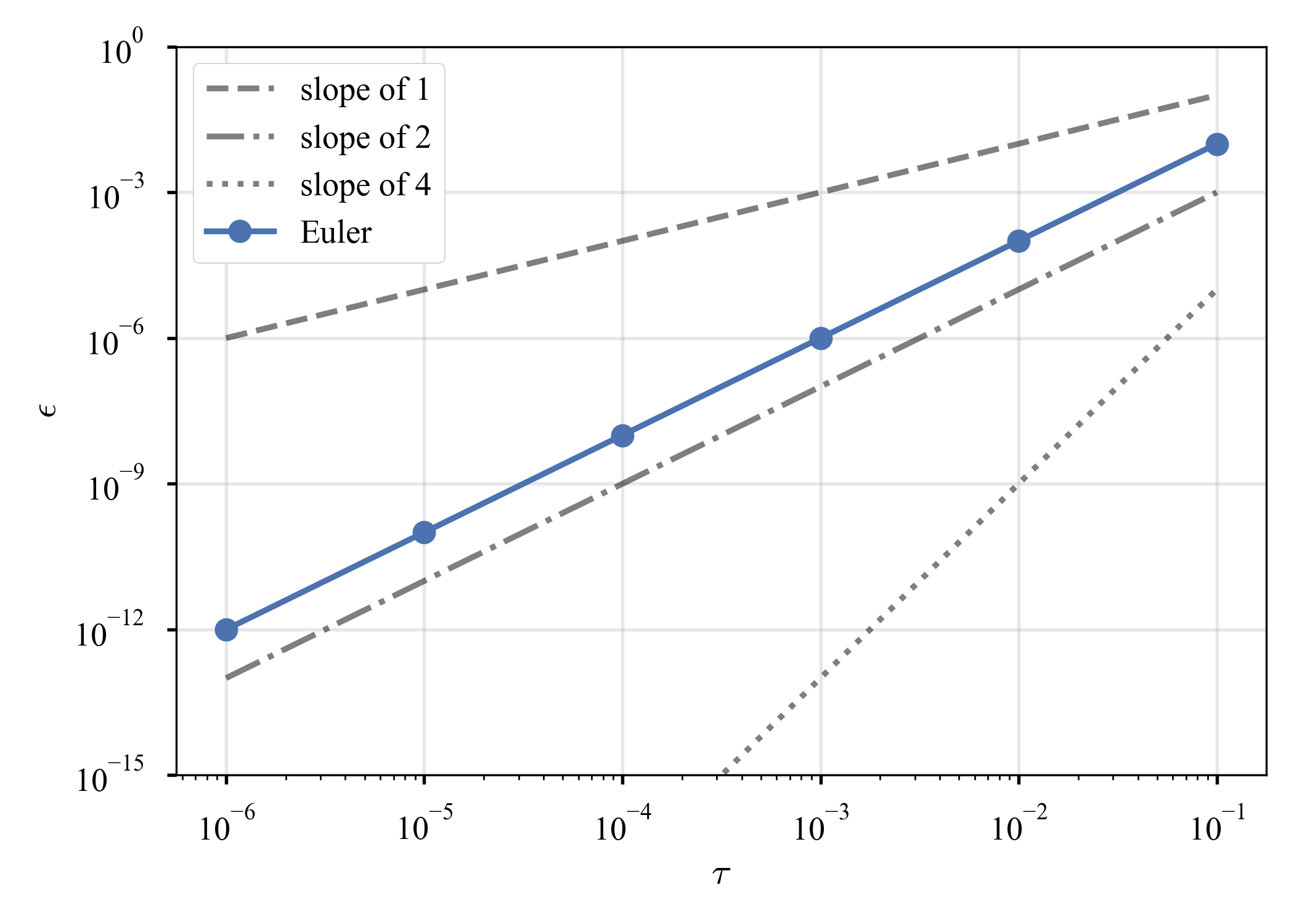
より,誤差項は$N \mathcal{O} \left( \tau^2 \right) \sim T / \tau \mathcal{O} \left( \tau^2 \right) \sim \mathcal{O} \left( \tau \right)$となるから,大域的には1次精度となる.
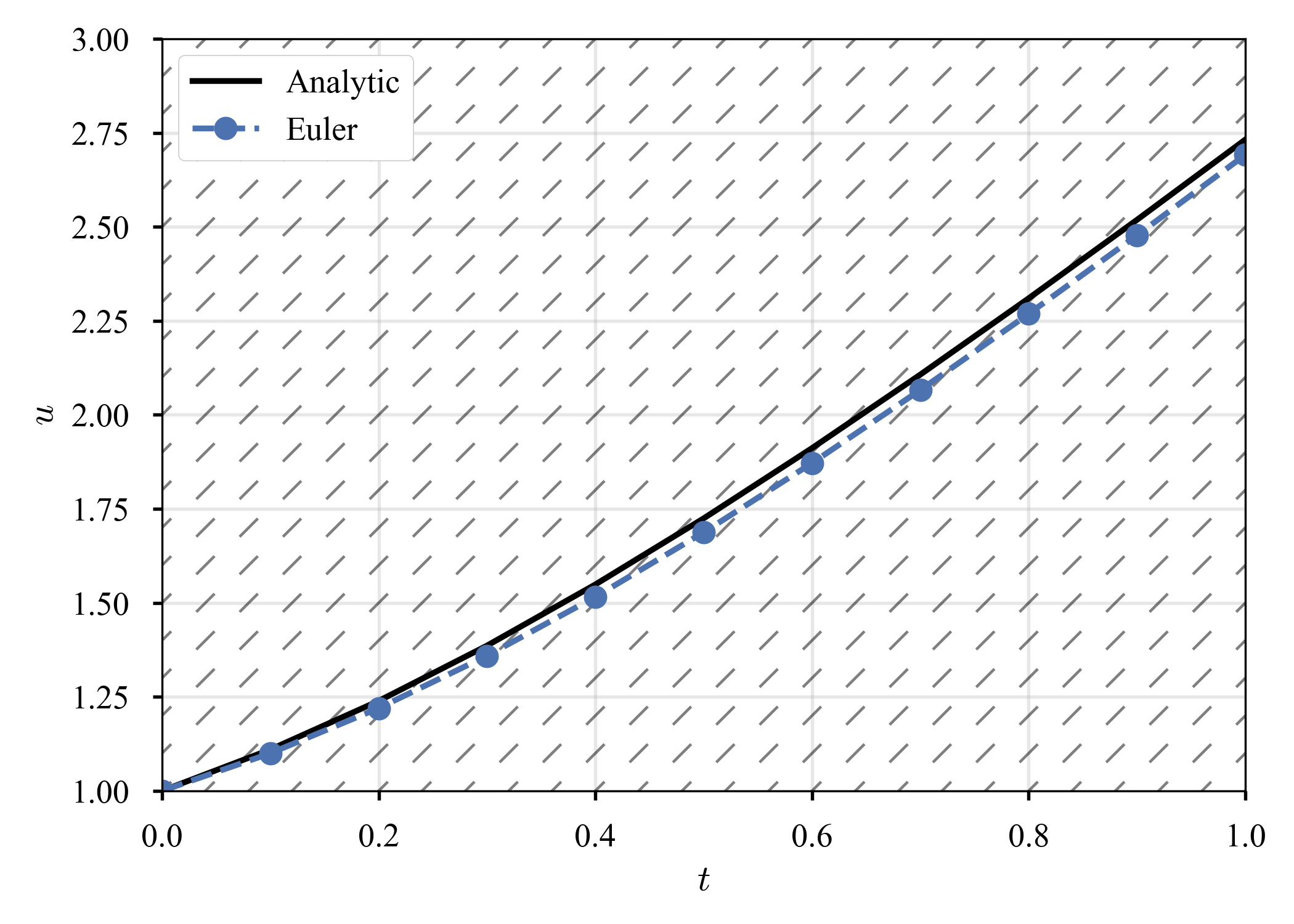
$t = \tau$での誤差と,$t = T = 1$での誤差を,時間刻みを変えながら記録すると,以下のようになる.
| $\text{Solution}$ | $\text{Error at } t=\tau$ | $\text{Error at } t=T$ |
|---|---|---|
 |
 |
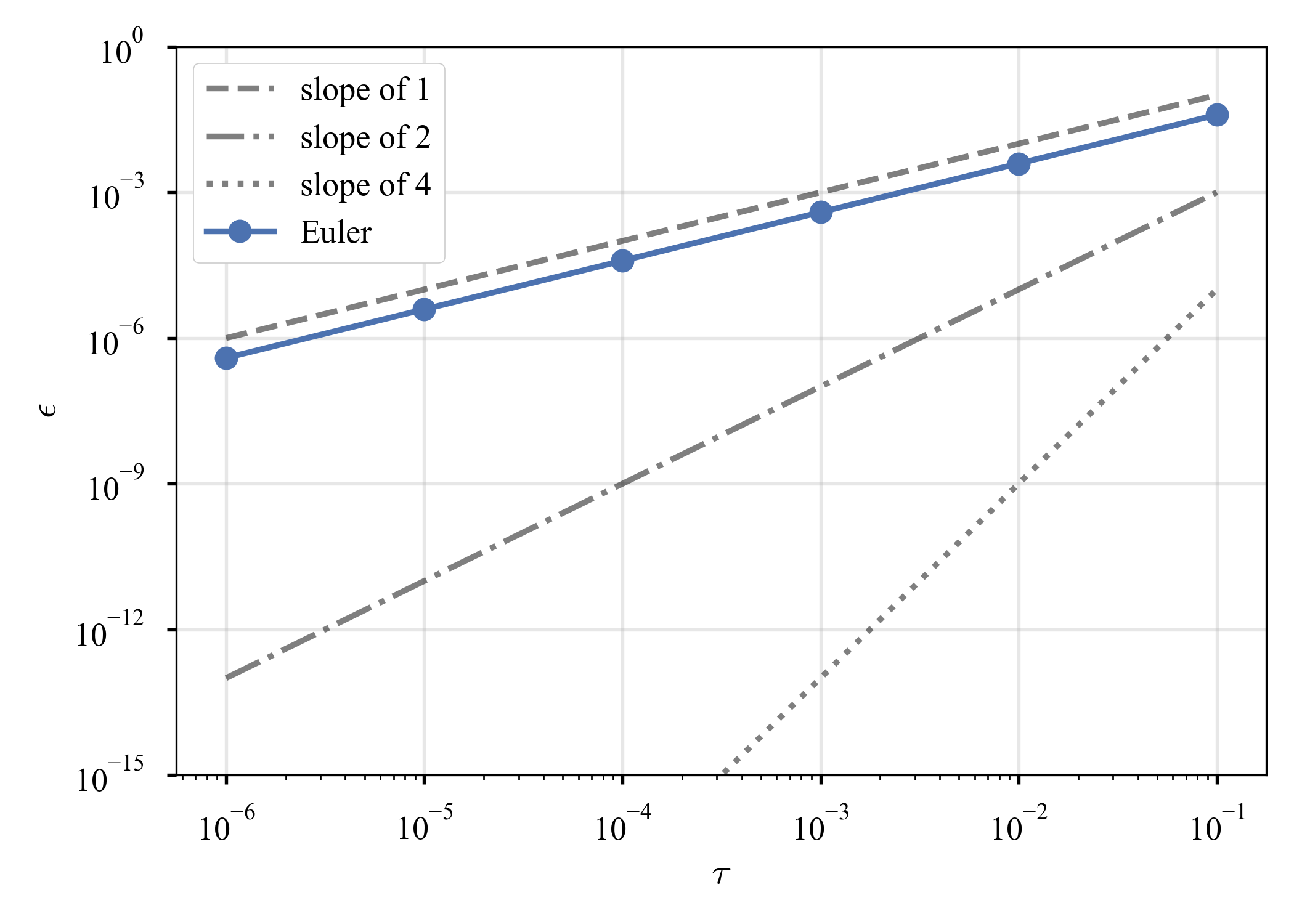 |
上記の議論はButcher2016: "201. Some numerical experiments"より借用したが,同書では,これは"an informal explanation"とされている.確かに,"誤差項が2つ累積するから$2 \mathcal{O} \left( \tau \right)$"など,大雑把すぎて怒られそうだ.厳密には,"211. Lobal truncation error","212. Global truncation error"で議論されているが,数学味が強く,私には良く理解できなかった.悔しいが,また知識を付けて帰って来よう.
Heun法
Karl Heunによる2次精度の方法.発音が難しそうだが,Wikipediaによると,"コイン"と言う気持ちで"ホイン".
"The "eu" is pronounced the same way as in "Euler", so "Heun" rhymes with "coin")".
\begin{align}
f_{1}
&= f \left( t^{(n)}, u^{(n)} \right) \\
f_{2}
&= f \left( t^{(n)} + \tau, u^{(n)} + \tau f_{1} \right) \\
u^{(n+1)}
&= u^{(n)} + \tau
\left(
\frac{f_1 + f_2}{2}
\right)
\end{align}
陽的Euler法を有効活用していると見ることができる.台形を計算しているとも言える(この視点からは,陽的Euler法は左手の長方形を計算している,陰的Euler法は右手).
Runge-Kutta法
Carl RungeとWilhelm Kuttaによる4次精度の方法.
\begin{align}
f_{1}
&= f \left( t^{(n)}, u^{(n)} \right) \\
f_{2}
&= f \left( t^{(n)} + \tau / 2, u^{(n)} + \tau f_{1} / 2 \right) \\
f_{3}
&= f \left( t^{(n)} + \tau / 2, u^{(n)} + \tau f_{2} / 2 \right) \\
f_{4}
&= f \left( t^{(n)} + \tau, u^{(n)} + \tau f_{3} \right) \\
u^{(n+1)}
&= u^{(n)} + \tau
\left(
\frac{f_{1} + 2 f_{2} + 2 f_{3} + f_{4}}{6}
\right)
\end{align}
陽的Runge-Kutta法はERK,陰的Runge-Kutta法はIRKと略されることが多い印象がある.こちらも本来は陽解法・陰解法,および段数・次数を明示的に区別すべきであるが,本稿では特に断らない限り,4段4次の陽的Runge-Kutta法のことを単にRunge-Kutta法とかRK(4)などと呼ぶことにする.
何次精度か?
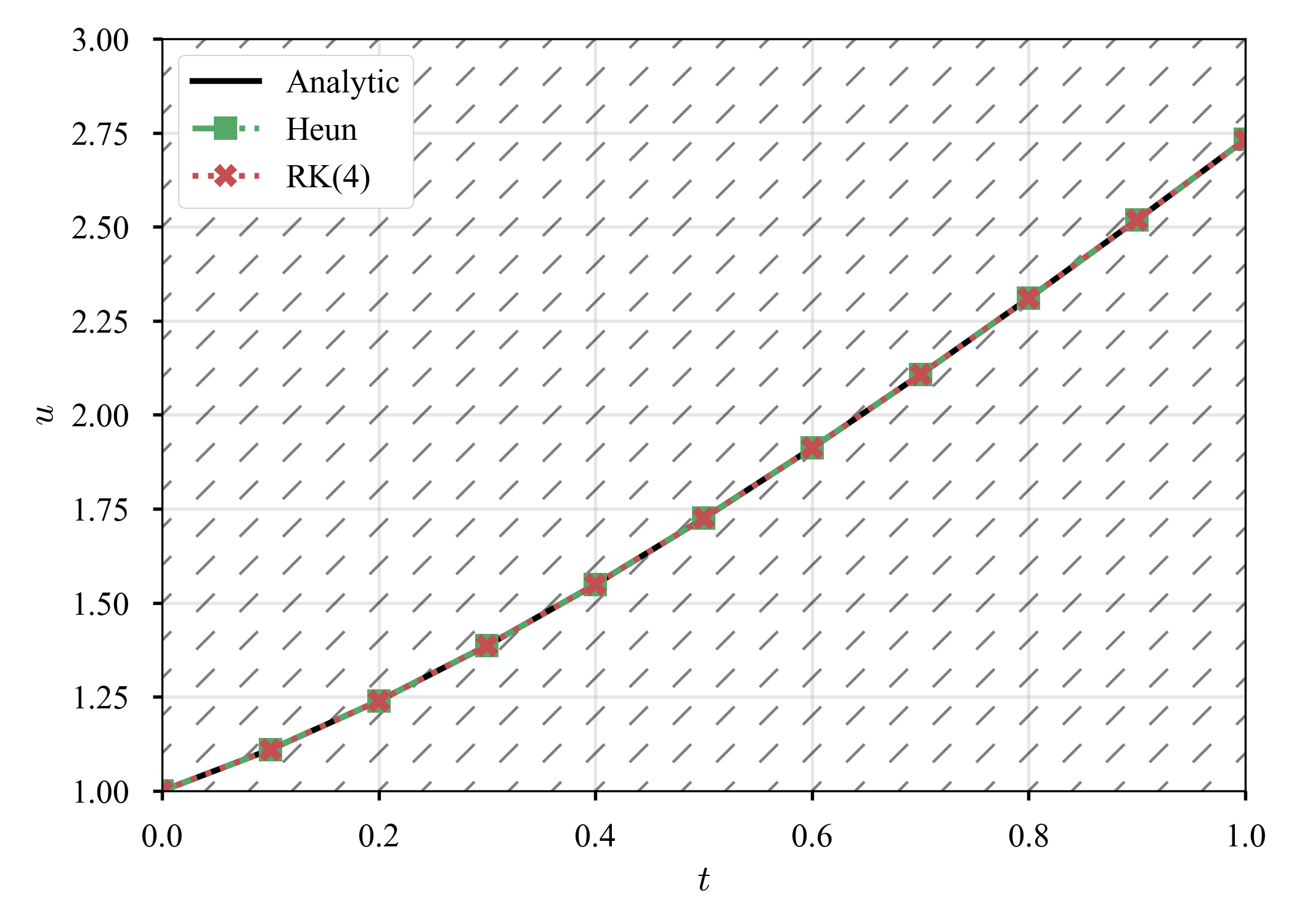
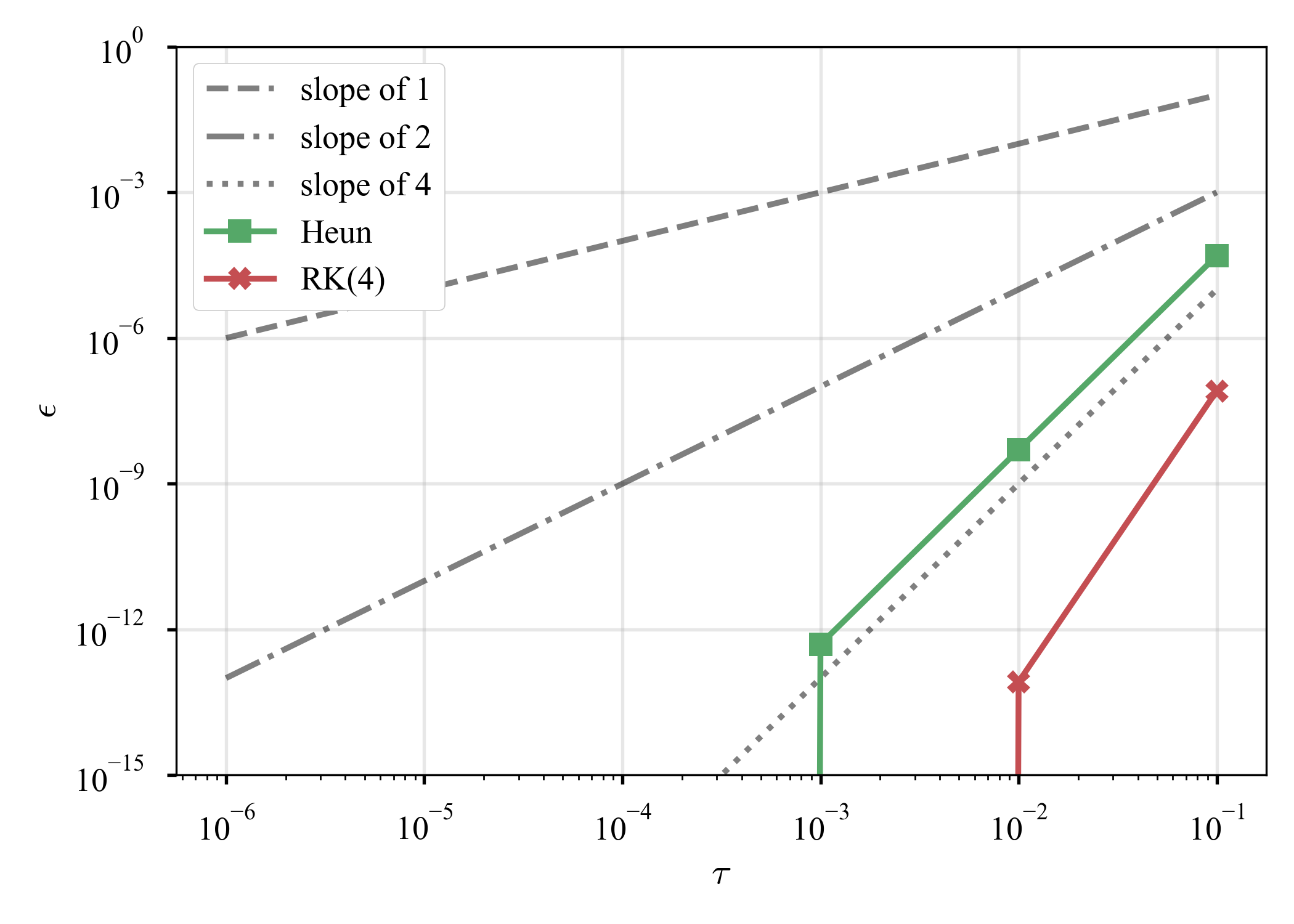
Euler法のときと同じ問題を考え,Heun法とRunge-Kutta法の誤差の収束具合を見る.
| $\text{Solution}$ | $\text{Error at } t=\tau$ | $\text{Error at } t=T$ |
|---|---|---|
 |
 |
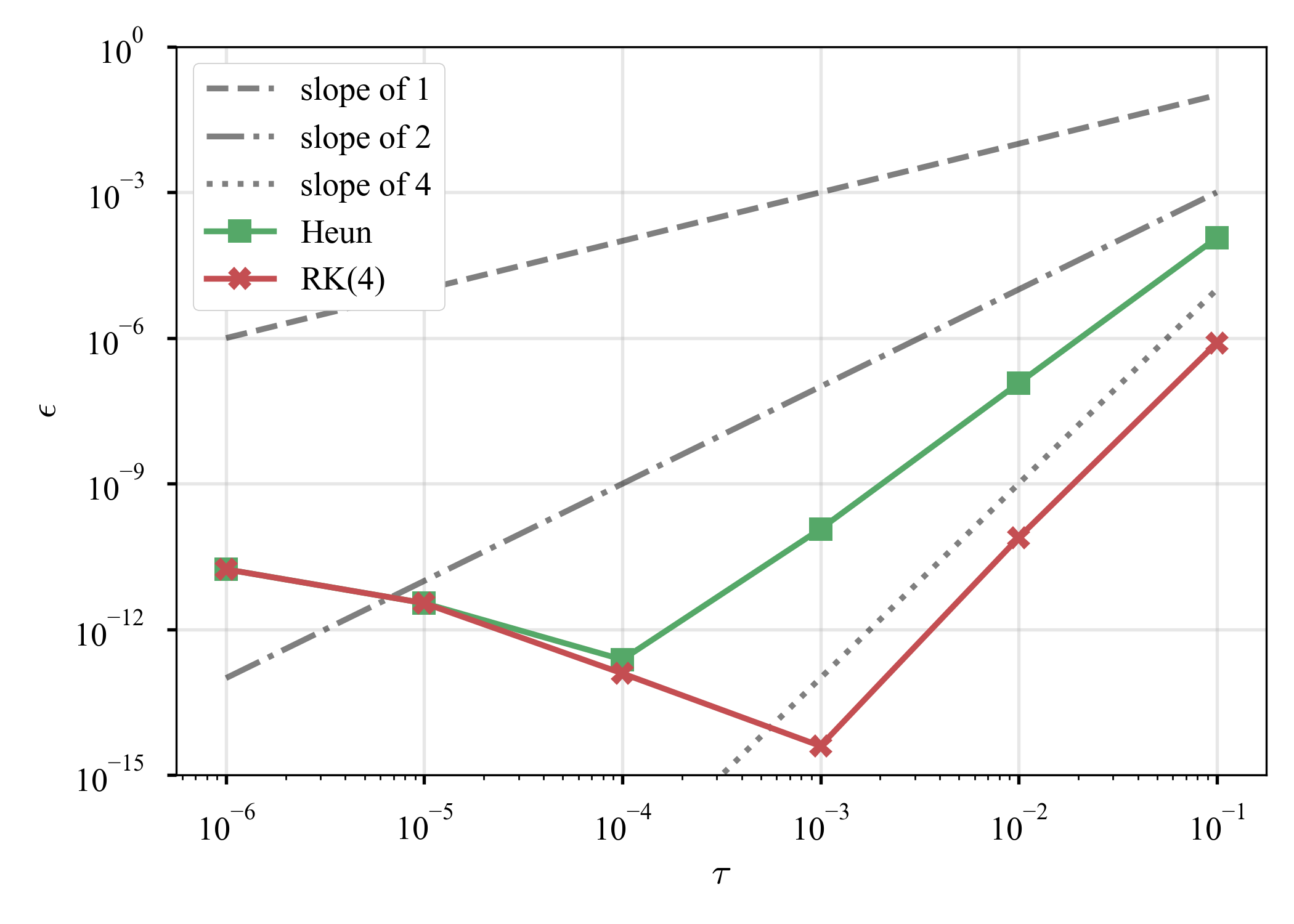 |
理論をサポートする結果だ(彼らが2次精度,4次精度ということを示すのは宿題にしておく).
Runge-Kutta Familyとして一般化
$s$段$p$次のRunge-Kutta法のことを,RK($s, p$)と呼ぶことにする($s$-stages $p$-th order Explicit Runge-Kutta method).このルールに則れば,上記の方法はRK(4, 4)という位置づけになる3.
平たく言えば,段数$s$は計算の大変さで,次数$p$は計算の正確さと解釈できる.段数$s$と次数$p$の間には,
| $p$ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| $\text{min } s$ | 1 | 2 | 3 | 4 | 6 | 7 | 9 | 11 |
なる関係がある.4段4次までは調子(というか都合?)が良いのだが,5次精度を達成するには少なくとも6段の計算を要するなど,段々と計算の大変さに見合った精度が出なくなってくる($s \ge p$だが$s = p$とは限らない, e.g., Butcher1965, Butcher1985).これが,4段4次の陽的Runge-Kutta法が広く浸透している理由であろう.
2段2次の方法
Heun法を再訪する.ところで,$\theta = 1$なるパラメータを導入して,以下のように書き改める(しかし,Heun法に他ならない).
\begin{align}
f_{1}
&= f \left( t^{(n)}, u^{(n)} \right) \\
f_{2}
&= f \left( t^{(n)} + \theta \tau, u^{(n)} + \theta \tau f_{1} \right) \\
u^{(n+1)}
&= u^{(n)} + \tau
\left(
\left( 1 - \frac{1}{2 \theta} \right) f_{1}
+ \frac{1}{2 \theta} f_{2}
\right)
\end{align}
$\theta = 1$は,上述のHeun法に一致する.$f_{2}$の評価が肝のように感じる.$\theta = 1 / 2$を選べば$t^{(n)} + \tau / 2$での値を使うことになり,これは中点法(mid-point method)と呼ばれる(なんとも名前通りの方法だね4).また,$\theta = 2 / 3$はRalston法(Ralston1962)と呼ばれる.$\theta \in [0, 1]$の選び方により,$f_{2}$の評価点を少しずつ動かしていると見える(何だか,$\theta$法やCrank–Nicolson法を思い出す).
Runge-Kutta法の一般化公式とButcher tableau
定義(例えば,Hairer+1993)
$s$を整数,$a_{21}, a_{31}, a_{32}, ..., a_{s1}, a_{s2}, ..., a_{s,s-1}$,$b_{1}, b_{2}, ..., b_{s}$,$c_{2}, c_{3}, ..., c_{s}$を実数とする.このとき,
\begin{align}
f_{1} &= f \left( t^{(n)}, u^{(n)} \right) \\
f_{2} &= f \left( t^{(n)} + c_{2} \tau, u^{(n)} + \tau a_{21} f_{1} \right) \\
f_{3} &= f \left( t^{(n)} + c_{3} \tau, u^{(n)} + \tau \left( a_{31} f_{1} + a_{32} f_{2} \right) \right) \\
\vdots \\
f_{s} &= f \left( t^{(n)} + c_{s} \tau, u^{(n)} + \tau \left( a_{s1} f_{1} + a_{s2} f_{2} + \cdots + a_{s,s-1} f_{s-1} \right) \right) \\
u^{(n+1)} &= u^{(n)} + \tau \left( b_{1} f_{1} + b_{2} f_{2} + \cdots + b_{s} f_{s} \right) \\
\end{align}
或いは,短く纏めて
\begin{align}
f_{k} &= f \left( t^{(n)} + c_{k} \tau, u^{(n)} + \tau \sum_{l=1}^{k-1} a_{k,l} f_{l} \right) \quad (\text{for } k = 1, 2, ..., s) \\
u^{(n+1)} &= u^{(n)} + \tau \sum_{m=1}^{s} b_{m} f_{m} \\
\end{align}
を,問題
\begin{align}
\frac{d}{dt} u \left( t \right)
&= f \left( t, u \right) \\
u \left( t^{(n)} \right)
&= u^{(n)} \\
\end{align}
に対する$s$段の陽的Runge-Kutta法(ERK)呼ぶ.このとき,$c_{i}$は,次の条件
\begin{align}
c_{2}
&= a_{21} \\
c_{3}
&= a_{31} + a_{32} \\
\vdots \\
c_{s}
&= a_{s1} + a_{s2} + \cdots + a_{s,s-1} \\
\end{align}
或いは,より簡単に
\begin{align}
c_{i}
&= \sum_{j=1}^{i-1} a_{ij} \quad (\text{for } i = 1, 2, ..., s) \\
\end{align}
を満たす.また,$b_{i}$はpartition of unityを成す.
これは,テーブルに起こすと見易い.Butcher1964により,今日,Butcher tableauと呼ばれるものが浸透している(空白はゼロを意味する).
\begin{array}
{c|cccccc}
0 \\
c_{2} & a_{21} \\
c_{3} & a_{31} & a_{32} \\
\vdots & \vdots & \vdots & \ddots \\
c_{s} & a_{s1} & a_{s2} & \cdots & a_{s, s-1} \\
\hline
& b_{1} & b_{2} & \cdots & b_{s-1} & b_{s}
\end{array}
$f_{s} = f \left( t^{(n)} + c_{s} \tau, \cdots \right)$より,$\boldsymbol{c}$は$f_{s}$をどこで評価するかを意味する.
$f_{s} = f \left( \cdots, u^{(n)} + \tau \sum_{k=1}^{s-1} a_{s,k} f_{k} \right)$より,$\boldsymbol{A}$は各ステージで計算した$f_{k}$が今のステージ$f_{s}$にどれだけ寄与するかを意味する.
$u^{(n+1)} = u^{(n)} + \tau \sum_{k=1}^{s} b_{k} f_{k}$より,$\boldsymbol{b}$は$f_{k}$に与える重みを意味する.
上記を纏めて考えると,これは重み付き求積法と見ることができる.$\boldsymbol{c}$は求積点(quadrature node),$\boldsymbol{b}$は求積重み(quadrature weight)ではないか.なんとも興味深い.
2段2次の方法
Butcher tableauを見ながら,$s=2$の場合を再訪する.
\begin{align}
f_{1} &= f \left( t^{(n)}, u^{(n)} \right) \\
f_{2} &= f \left( t^{(n)} + c_{2} \tau, u^{(n)} + \tau a_{21} f_{1} \right) \\
u^{(n+1)} &= u^{(n)} + \tau \left( b_{1} f_{1} + b_{2} f_{2} \right) \\
\end{align}
適合条件は,
\begin{align}
c_{2}
= a_{21}, \
b_{1} + b_{2}
= 1 \\
\end{align}
である(RK(2, 2)).上述の,$\theta$を導入して改めた式と辻褄が合う.代表的なRK(2, 2)は既に記したので,再掲しない.
3段3次の方法
Butcher tableauを見ながら,$s=3$の場合を書き下す.
\begin{align}
f_{1} &= f \left( t^{(n)}, u^{(n)} \right) \\
f_{2} &= f \left( t^{(n)} + c_{2} \tau, u^{(n)} + \tau a_{21} f_{1} \right) \\
f_{3} &= f \left( t^{(n)} + c_{3} \tau, u^{(n)} + \tau \left( a_{31} f_{1} + a_{32} f_{2} \right) \right) \\
u^{(n+1)} &= u^{(n)} + \tau \left( b_{1} f_{1} + b_{2} f_{2} + b_{3} f_{3} \right) \\
\end{align}
適合条件は,
\begin{align}
c_{2}
= a_{21}, \
c_{3}
= a_{31} + a_{32}, \
b_{1} + b_{2} + b_{3}
= 1 \\
\end{align}
である(と思うが,少し自信が無い,,,勉強し直そうと思う).
列挙すること自体は余り重要に感じないが,,,取り敢えず,Butcher tableauの読み方の練習のために,幾つかの有名な方法を記す.List of Runge-Kutta methodsと併せて見ると良い.
Heunの方法
\begin{align}
f_{1} &= f \left( t^{(n)}, u^{(n)} \right) \\
f_{2} &= f \left( t^{(n)} + \tau / 3, u^{(n)} + \tau f_{1} / 3 \right) \\
f_{3} &= f \left( t^{(n)} + 2 \tau / 3, u^{(n)} + \tau 2 f_{2} / 3 \right) \\
u^{(n+1)} &= u^{(n)} + \tau \left( f_{1} + 3 f_{3} \right) / 4 \\
\end{align}
Kuttaの方法
\begin{align}
f_{1} &= f \left( t^{(n)}, u^{(n)} \right) \\
f_{2} &= f \left( t^{(n)} + \tau / 2, u^{(n)} + \tau f_{1} / 2 \right) \\
f_{3} &= f \left( t^{(n)} + \tau, u^{(n)} + \tau \left( - f_{1} + 2 f_{2} \right) \right) \\
u^{(n+1)} &= u^{(n)} + \tau \left( f_{1} + 4 f_{2} + f_{3} \right) / 6 \\
\end{align}
Ralstonの方法
\begin{align}
f_{1} &= f \left( t^{(n)}, u^{(n)} \right) \\
f_{2} &= f \left( t^{(n)} + \tau / 2, u^{(n)} + \tau f_{1} / 2 \right) \\
f_{3} &= f \left( t^{(n)} + 3 \tau / 4, u^{(n)} + 3 \tau f_{2} / 4 \right) \\
u^{(n+1)} &= u^{(n)} + \tau \left( 2 f_{1} + 3 f_{2} + 4 f_{3} \right) / 9 \\
\end{align}
SSP-RK(3)
\begin{align}
f_{1} &= f \left( t^{(n)}, u^{(n)} \right) \\
f_{2} &= f \left( t^{(n)} + \tau, u^{(n)} + \tau f_{1} \right) \\
f_{3} &= f \left( t^{(n)} + \tau / 2, u^{(n)} + \tau \left( f_{1} + f_{2} \right) / 4 \right) \\
u^{(n+1)} &= u^{(n)} + \tau \left( f_{1} + f_{2} + 4 f_{3} \right) / 6 \\
\end{align}
4段4次の方法
既に記した4段4次の陽的Runge-Kutta法のほかに,Kuttaの1/8則とか3/8則と呼ばれるものも知られている.
\begin{align}
f_{1}
&= f \left( t^{(n)}, u^{(n)} \right) \\
f_{2}
&= f \left( t^{(n)} + \tau / 3, u^{(n)} + \tau f_{1} / 3 \right) \\
f_{3}
&= f \left( t^{(n)} + 2 \tau / 3, u^{(n)} + \tau \left( - f_{1} / 3 + f_{2} \right) \right) \\
f_{4}
&= f \left( t^{(n)} + \tau, u^{(n)} + \tau \left( f_{1} - f_{2} + f_{3} \right) \right) \\
u^{(n+1)}
&= u^{(n)} + \tau
\left(
\frac{f_{1} + 3 f_{2} + 3 f_{3} + f_{4}}{8}
\right)
\end{align}
RK(4)とこの方法は同程度の精度を達成するが,実装が簡単で理解も明解な前者が好まれ,良く浸透している(埋め込み型を含め,高次のRK族も知られている, e.g., Dormand&Prince1980, が,ひえぇ実装が怖い).本稿の数値実験でも,前者を使う(が,きちんと4次精度が出ることは数値的に確認した).
安定性
安定性を考える(議論のタイミングがしっちゃかめっちゃかな気もするが,,,).線形な問題を考える.
\begin{align}
\frac{d}{d t} u \left( t \right)
&= M u \left( t \right) \\
u \left( 0 \right)
&= u^{(0)}
\end{align}
ここで,$M$は適当なJordan標準形とする(そうでないならば$v = N u$などと変換すれば良い,或いは変換しなくともスペクトル半径の議論に持ち込めば良いのではないかな,,,結局同じことかもしれないが,,,).
一般解を導く.
\begin{align}
\frac{d u}{u}
&= M d t \\
\ln \left( u \right)
&= M t + C \\
u \left( t \right)
&= C \exp \left( M t \right) \\
\end{align}
初期値を与えれば,$u \left( t \right) = u^{(0)} \exp \left( M t \right)$.或いは,$u \left( t^{(n)} \right) = u^{(0)} \exp \left( n \tau M \right)$.数値解との区別のため,この解析解のことを$U$と呼ぶことにする.
解析解の1ステップの間での増幅率を
\begin{align}
G
&= \frac{U^{(n+1)}}{U^{(n)}} \\
&= \frac{u^{(0)} \exp \left( (n+1) \tau M \right)}
{u^{(0)} \exp \left( n \tau M \right)} \\
&= \exp \left( \tau M \right) \\
&= I + \tau M + \frac{\tau^2}{2!} M^2 + \frac{\tau^3}{3!} M^3 + \cdots
\end{align}
と定義する.行列の指数関数をゼロ周りでTaylor展開(Maclaurin展開)した.$| G | \gt 1$では,$U$が段々と大きくなって発散する.$U$が収束するためには,$| G | \le 1$.
Euler法を考える.
\begin{align}
u^{(1)}
&= u^{(0)} + \tau M u^{(0)}
= \left( I + \tau M \right) u^{(0)} \\
u^{(2)}
&= u^{(1)} + \tau M u^{(1)}
= \left( I + \tau M \right) u^{(1)} \\
\vdots \\
u^{(n)}
&= u^{(n-1)} + \tau M u^{(n-1)}
= \left( I + \tau M \right)^{n} u^{(0)} \\
\end{align}
増幅率は,
\begin{align}
G_{\text{Euler}}
&= \frac{u^{(n+1)}}{u^{(n)}} \\
&= \frac{\left( I + \tau M \right)^{n+1} u^{(0)}}
{\left( I + \tau M \right)^{n} u^{(0)}} \\
&= I + \tau M \\
&= I + z \quad \left( z := \tau M \right)
\end{align}
発散しないためには,$G_{\text{Euler}} = G_{\text{Euler}} (z)$が
\begin{align}
\lvert G_{\text{Euler}} (z) \rvert
&= \lvert I + z \rvert
\le 1
\end{align}
を満たす必要がある.より一般に,陽的Runge-Kutta法たちに対して$G_{\text{RK($s, p$)}}$が計算できて,
\begin{align}
S
&= \lbrace z \in \mathbb{C} \ ; \lvert G_{\text{RK($s, p$)}} (z) \rvert \le 1 \rbrace
\end{align}
を絶対安定領域と呼び,
\begin{align}
\tau M \in S
\implies
u^{(n)} \xrightarrow{n \to + \infty} 0
\end{align}
が成り立つ.絶対安定領域が左半平面$\lbrace z \in \mathbb{C} \ ; \mathrm{Re} (z) \le 1 \rbrace$を含むとき,その時間積分法をA-安定という.
2段2次のHeun法では,
\begin{align}
u^{(n+1)}
&= u^{(n)} + \tau
\left(
\frac{M u^{(n)} + M \left( u^{(n)} + \tau M u^{(n)} \right)}{2}
\right) \\
&= \left( I + \tau M + \frac{\left( \tau M \right)^2}{2} \right) u^{(n)} \\
\end{align}
より,
\begin{align}
G_{\text{Heun(2,2)}}
&= I + \tau M + \frac{\left( \tau M \right)^2}{2} \\
&= I + z + \frac{z^2}{2} \\
\end{align}
から,
\begin{align}
S_{\text{Heun(2,2)}}
&= \lbrace z \in \mathbb{C} \ ; \lvert G_{\text{Heun(2,2)}} (z) \rvert \le 1 \rbrace
\end{align}
が絶対安定領域である.
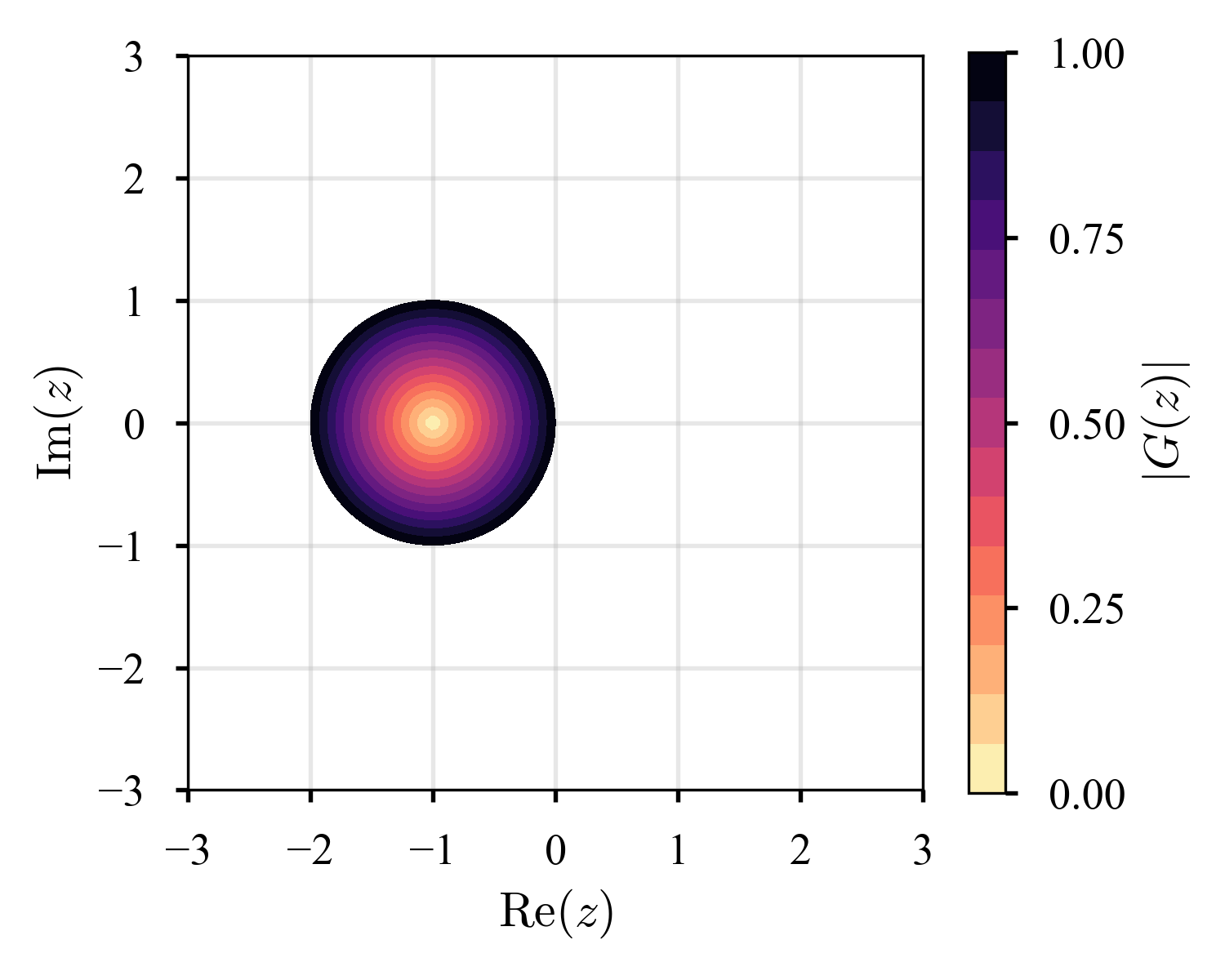
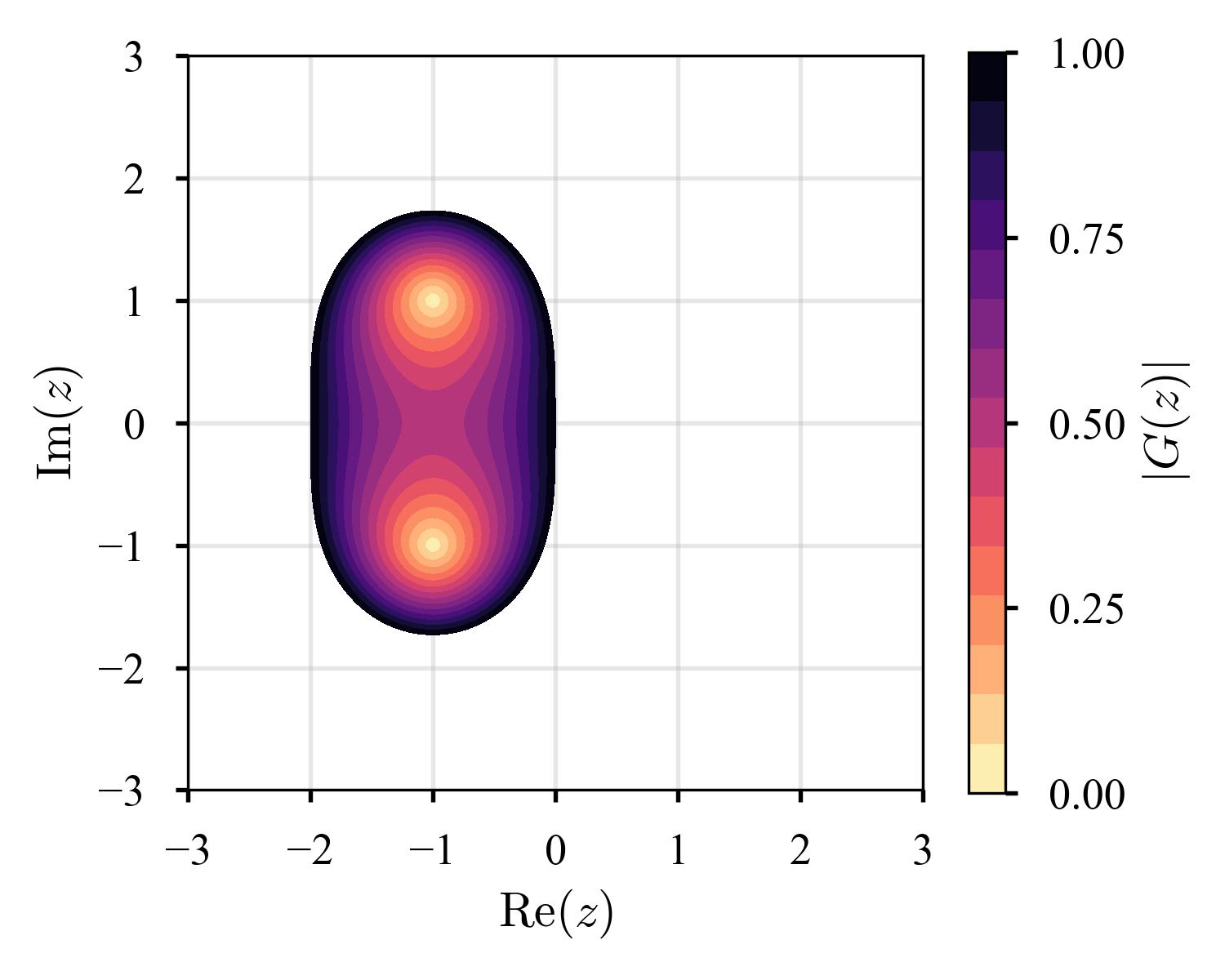
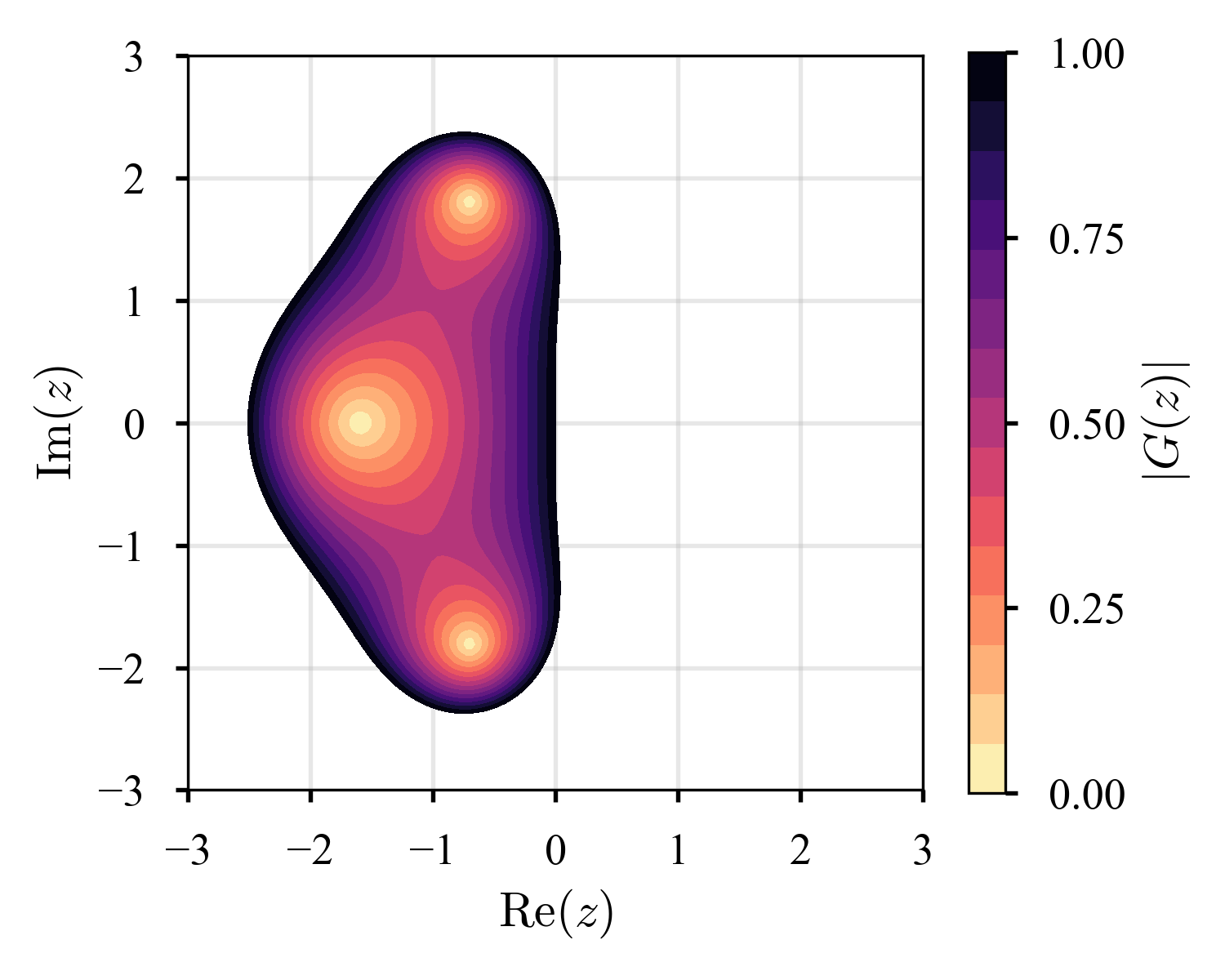
幾つかの陽的Runge-Kutta法の絶対安定領域を可視化すると,以下のようになる.$\tau M = z$が色の付いている領域にあれば安定,そうでないならば不安定である.
| $s=p=1$ | $s=p=2$ | $s=p=3$ | $s=p=4$ |
|---|---|---|---|
 |
 |
 |
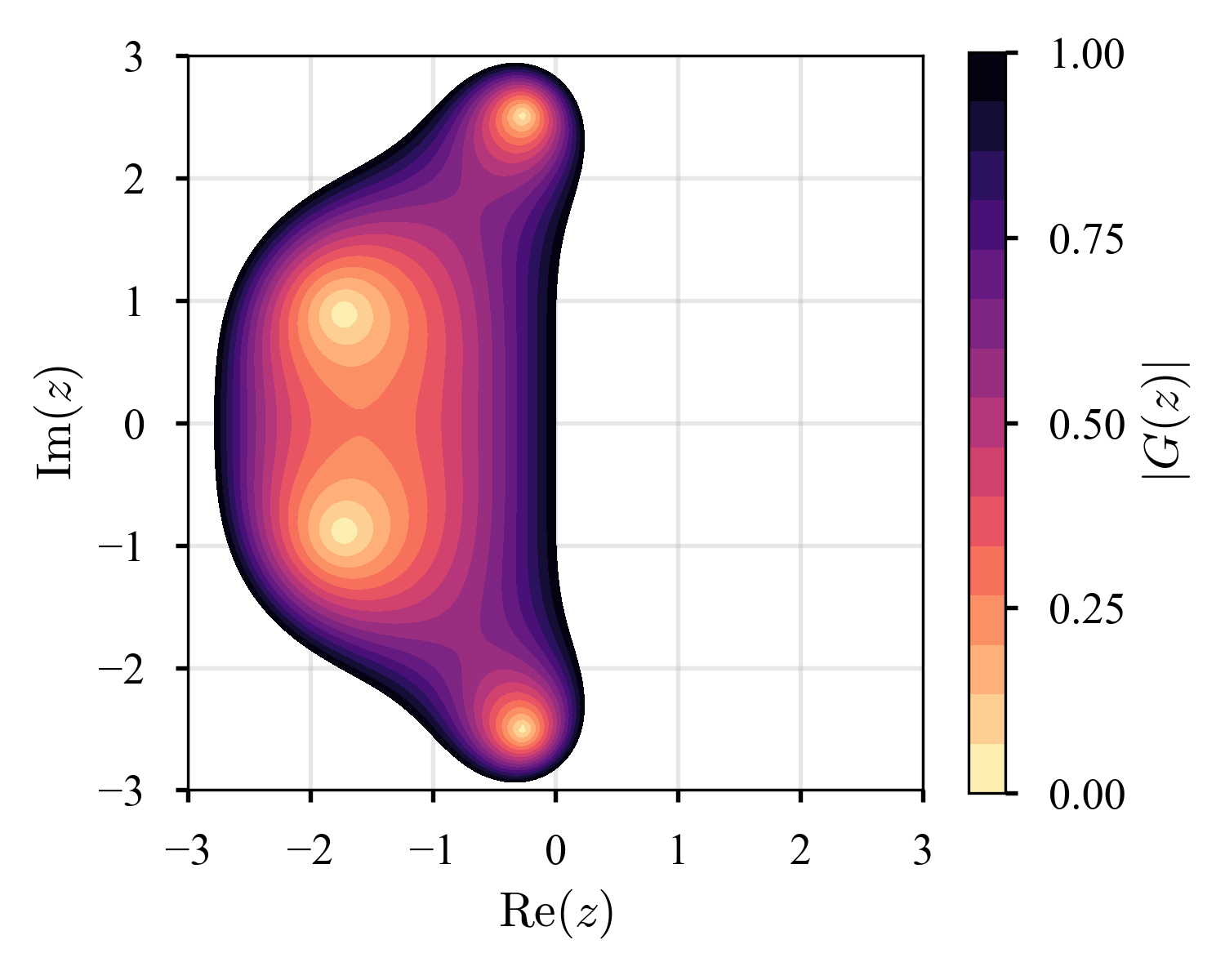 |
高次の方法ほど,絶対安定領域が拡大している.が,陽的Runge-Kutta法はA-stableでないことが示されているらしい.また,本稿では議論の対象としていないが,一般に,陰解法の安定性領域は陽解法のそれより大きい(cf. こちらの記事で議論されている,安定すぎて困ることもある,というのは興味深い).
Results
簡単な例
硬くない場合
簡単な指数減衰
\begin{align}
\frac{d}{d t} u \left( t \right)
&= - u \\
u \left( 0 \right)
&= 1 \\
\end{align}
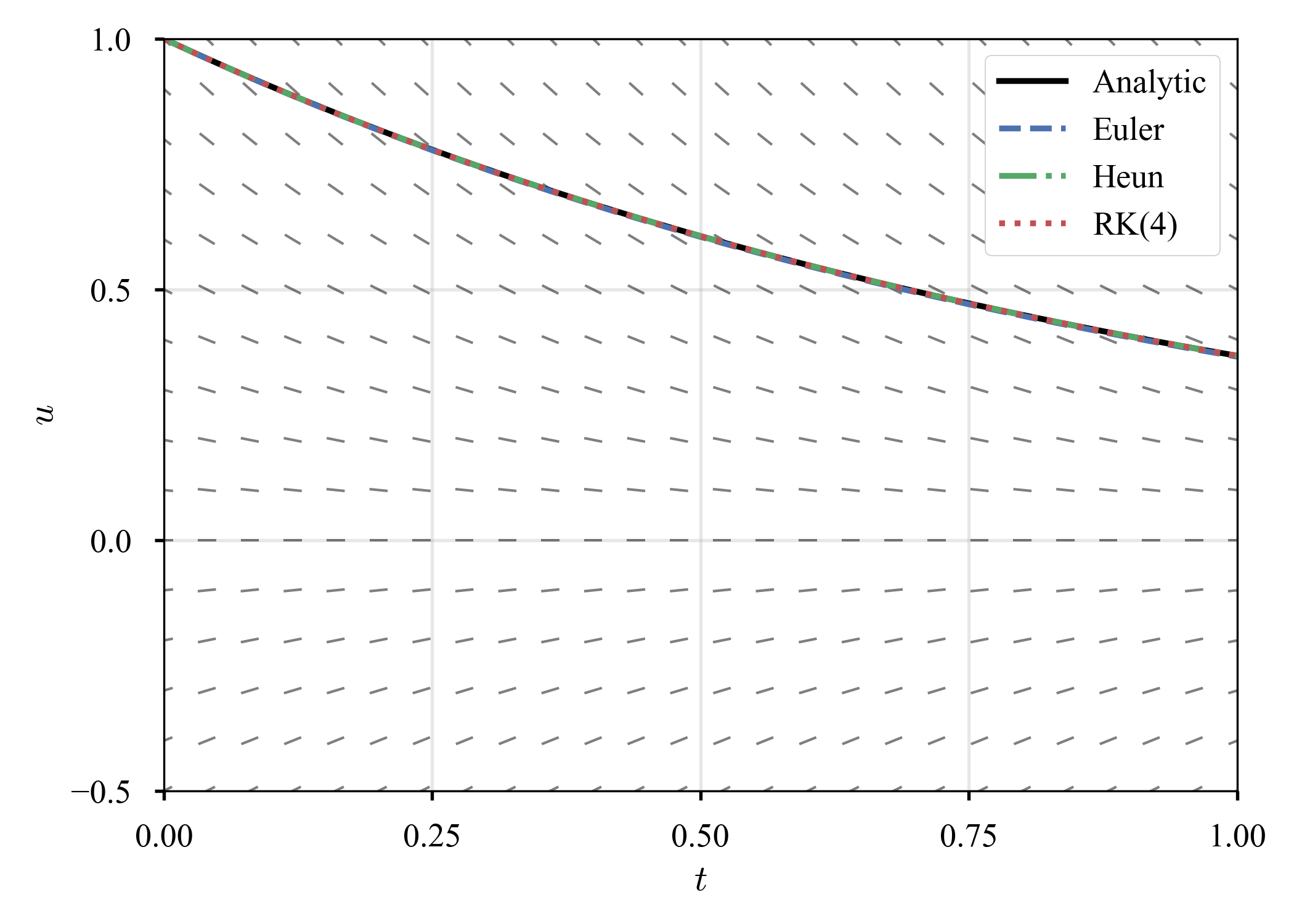
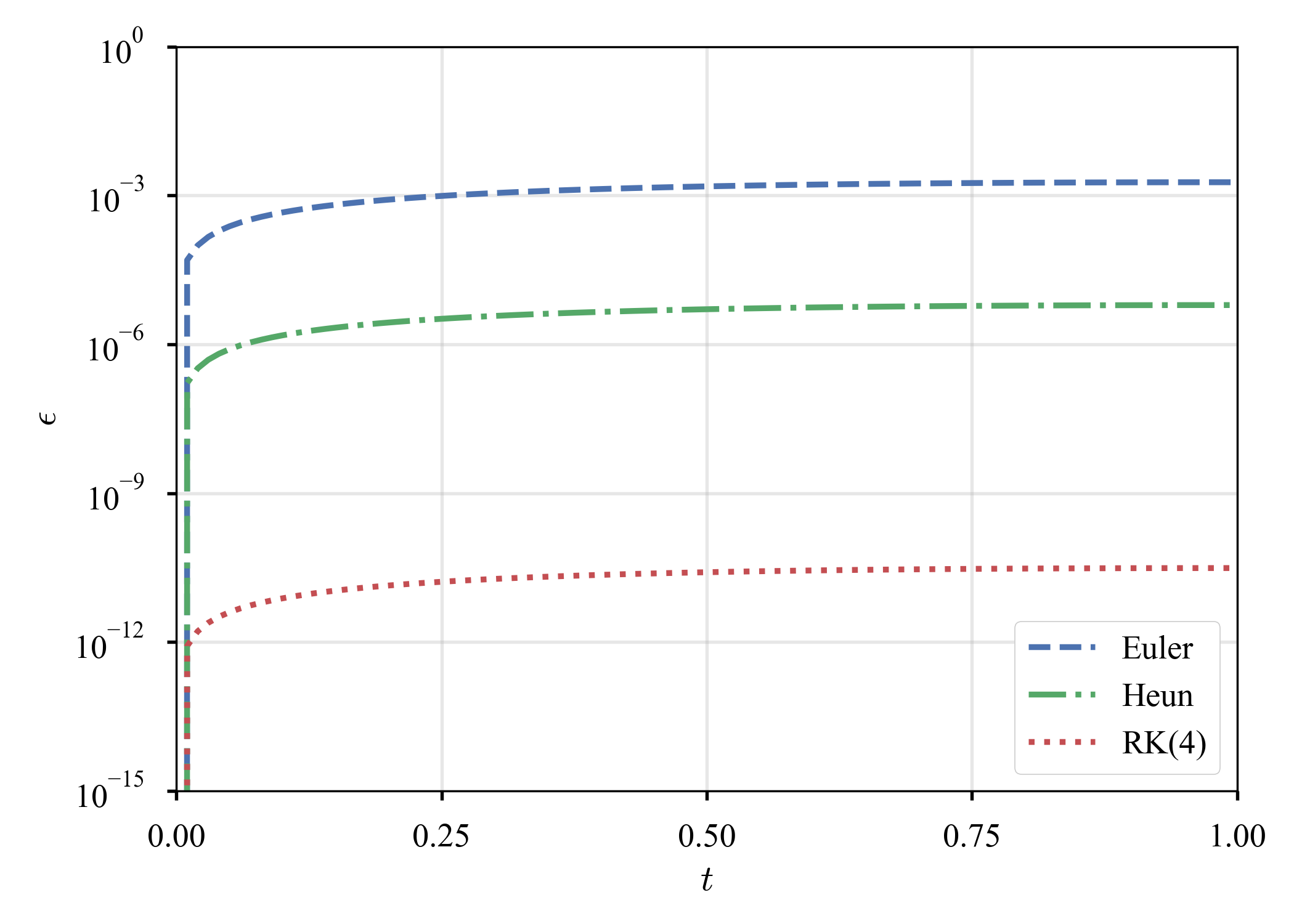
を考えると,解析解は$u = \exp (- t)$.$\tau = 10^{-2}$での結果と,$\tau$の選び方による誤差の減衰の傾向を見る.
| $u \left( t \right)$ | $\epsilon \left( t \right)$ | $\tau \text{ vs. } \epsilon \left( T \right)$ |
|---|---|---|
 |
 |
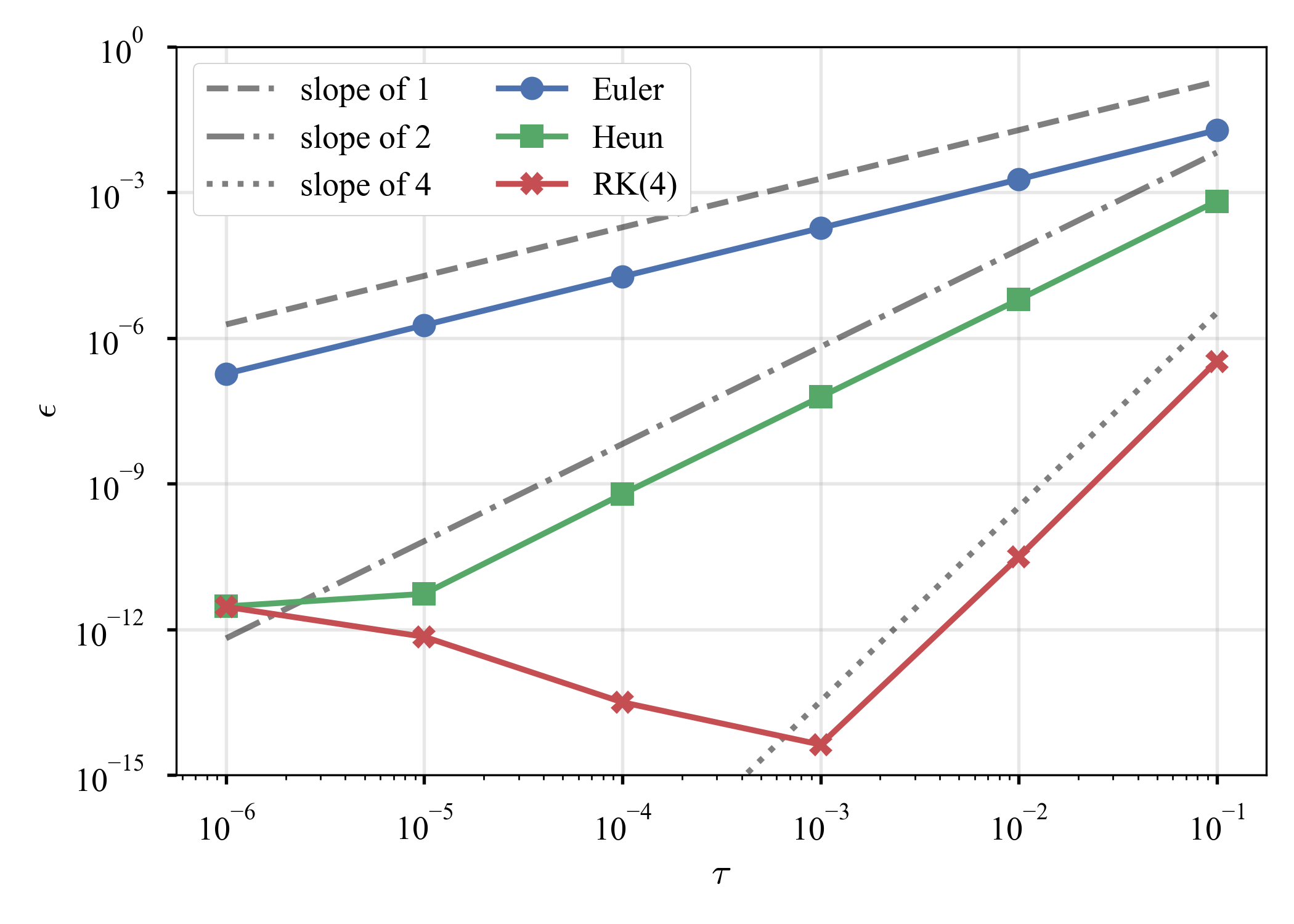 |
凡そ良く合致している.また,Euler法,Heun法,RK(4)がそれぞれ,1次,2次,4次の収束速度を持っていることも確認できる.
硬い場合
指数減衰
\begin{align}
\frac{d}{d t} u \left( t \right)
&= - 15 u \\
u \left( 0 \right)
&= 1 \\
\end{align}
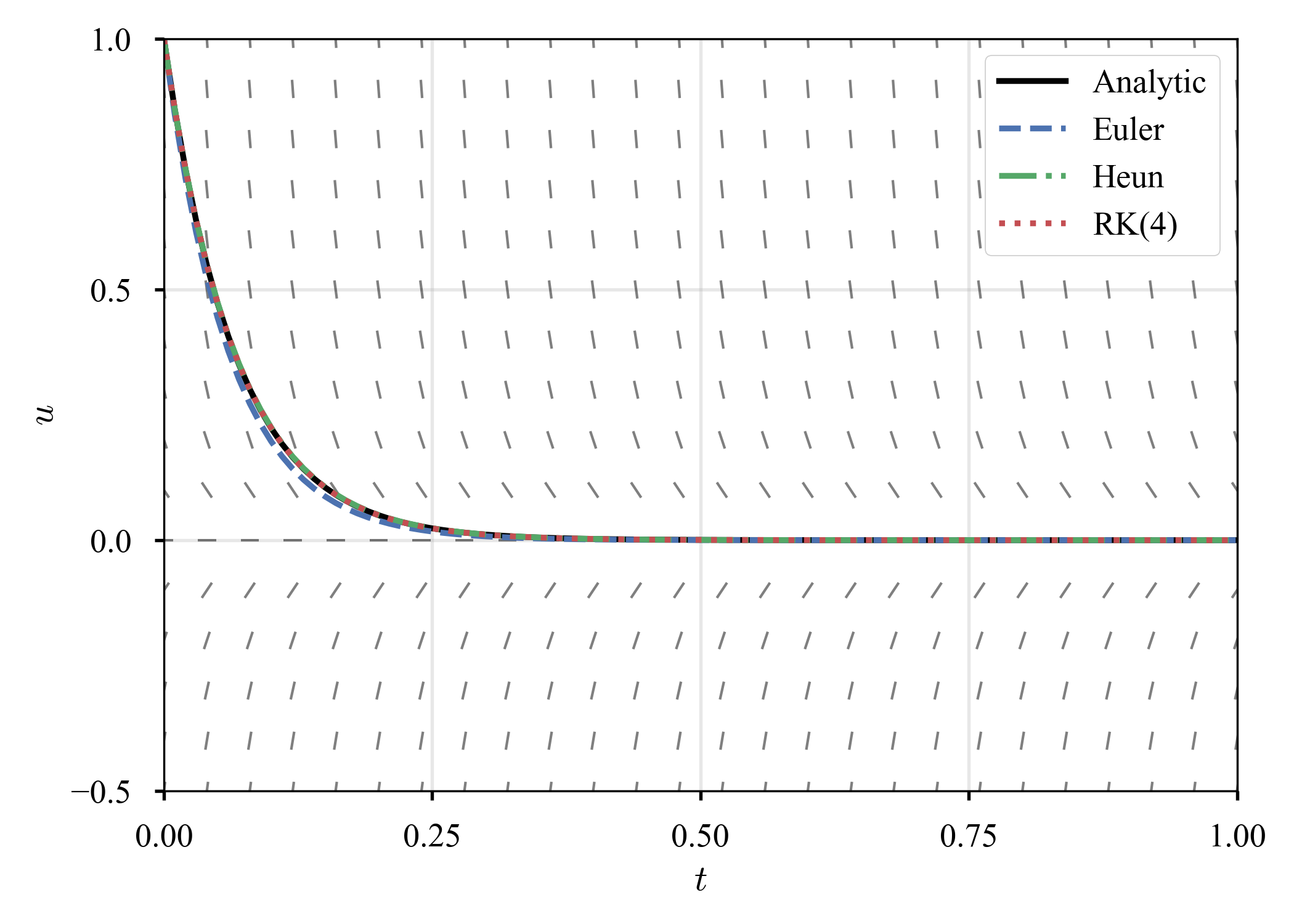
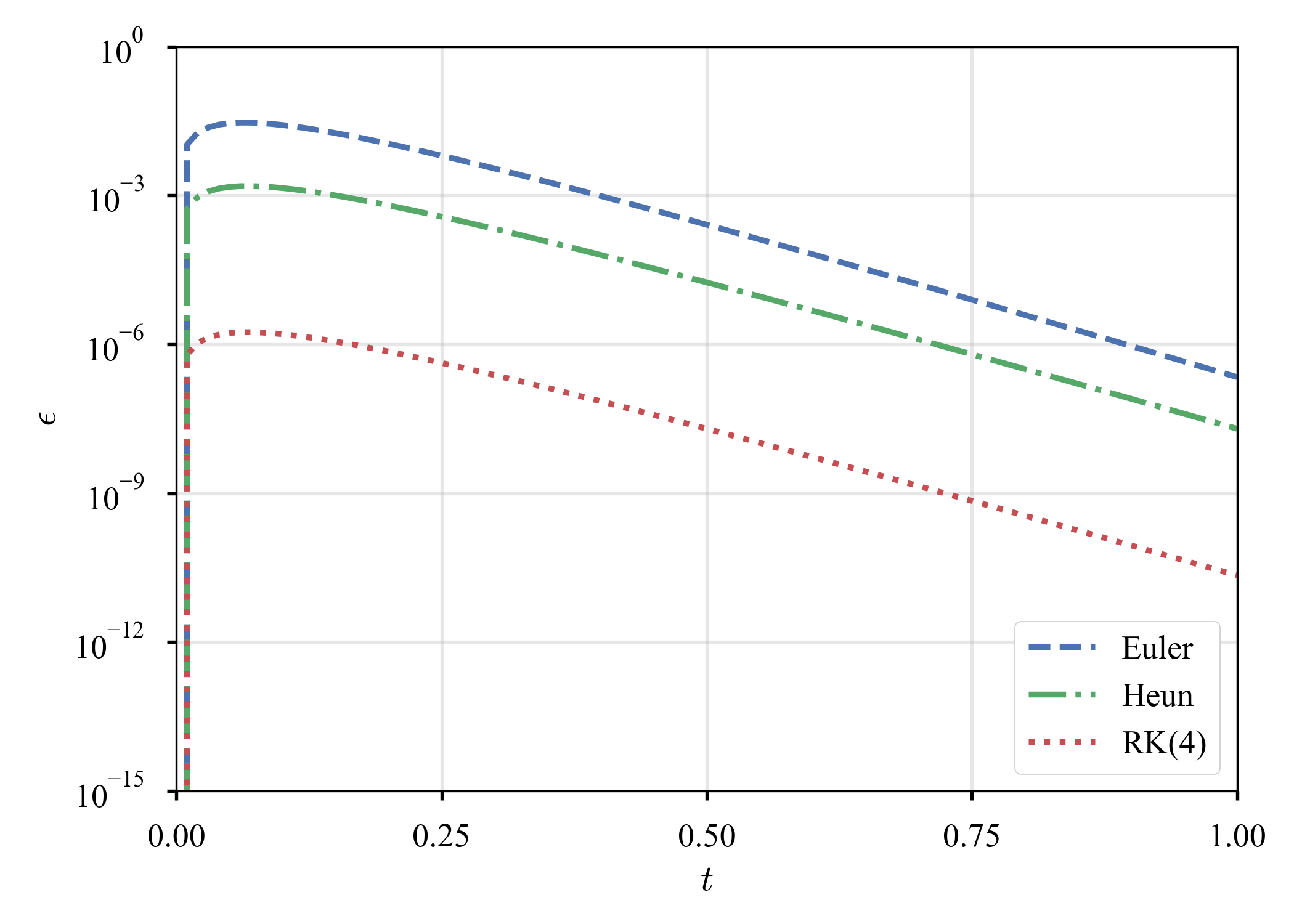
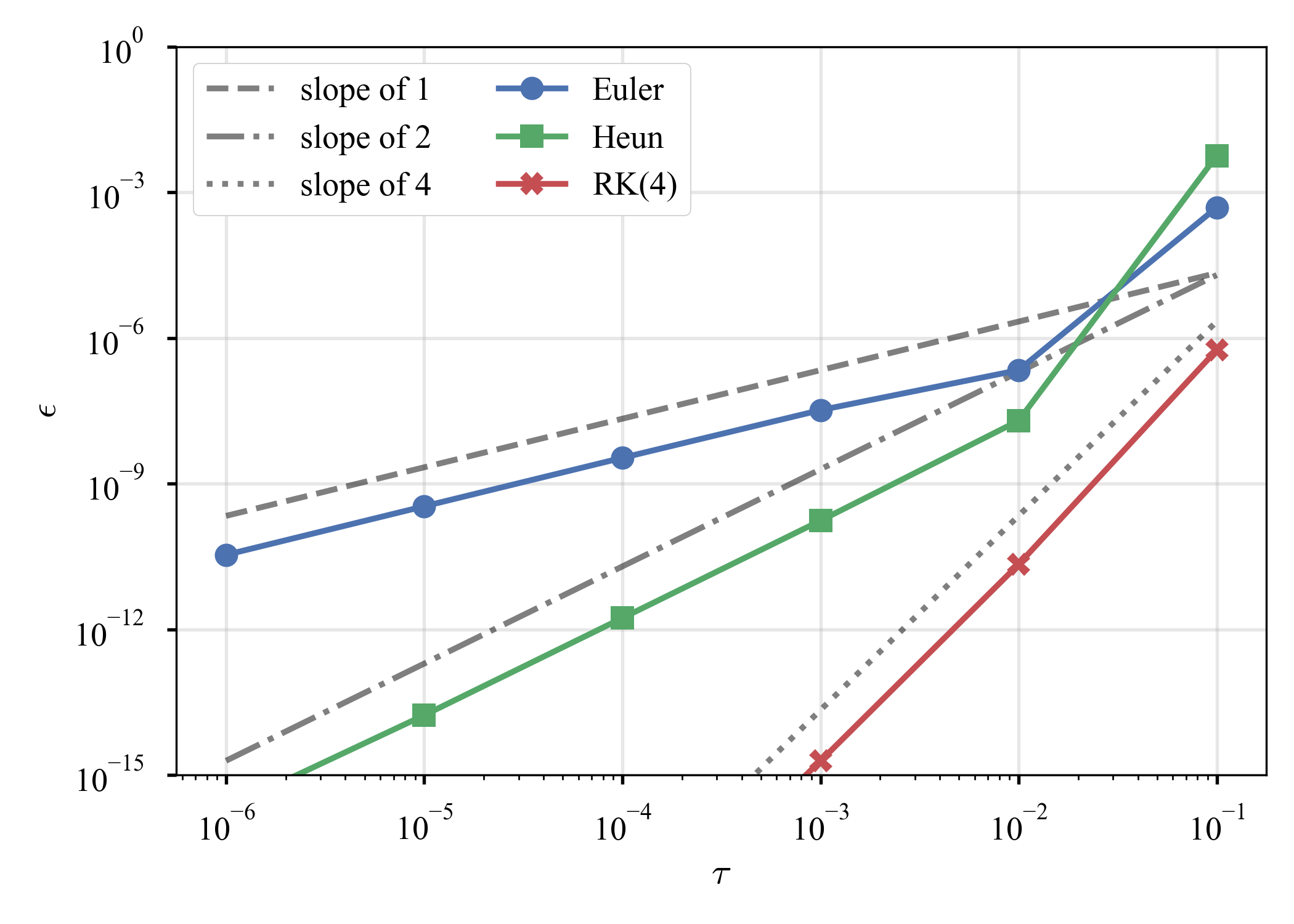
は,硬い方程式(stiff equation)と呼ばれる.解析解は$u = \exp (- 15 t)$.暫く調べたが,「硬い」の定義は意外と曖昧なのだそうだ.或いは,調べ切れていないだけかもしれないが,今のところは,陽解法では時間増分$\tau$を細かく取らなければ現象をcaptureできない,陰解法の方が好ましいものを硬いと呼ぶ,と大雑把に解釈しておく(関連の記事を見つけたが,良く理解できなかった,,).取り敢えず,先程と同じく,$\tau = 10^{-2}$での結果と,$\tau$の選び方による誤差の減衰の傾向を見る.
| $u \left( t \right)$ | $\epsilon \left( t \right)$ | $\tau \text{ vs. } \epsilon \left( T \right)$ |
|---|---|---|
 |
 |
 |
先程と異なり,$t \in (0, 0.1)$辺りに大きい誤差が出る.また,$\tau = 10^{-1}$のときだけ,誤差が大きい.$\tau = 10^{-1}$での解の軌跡を見てみる.
| $\dot{u} = - u$ | $\dot{u} = - 15 u$ |
|---|---|
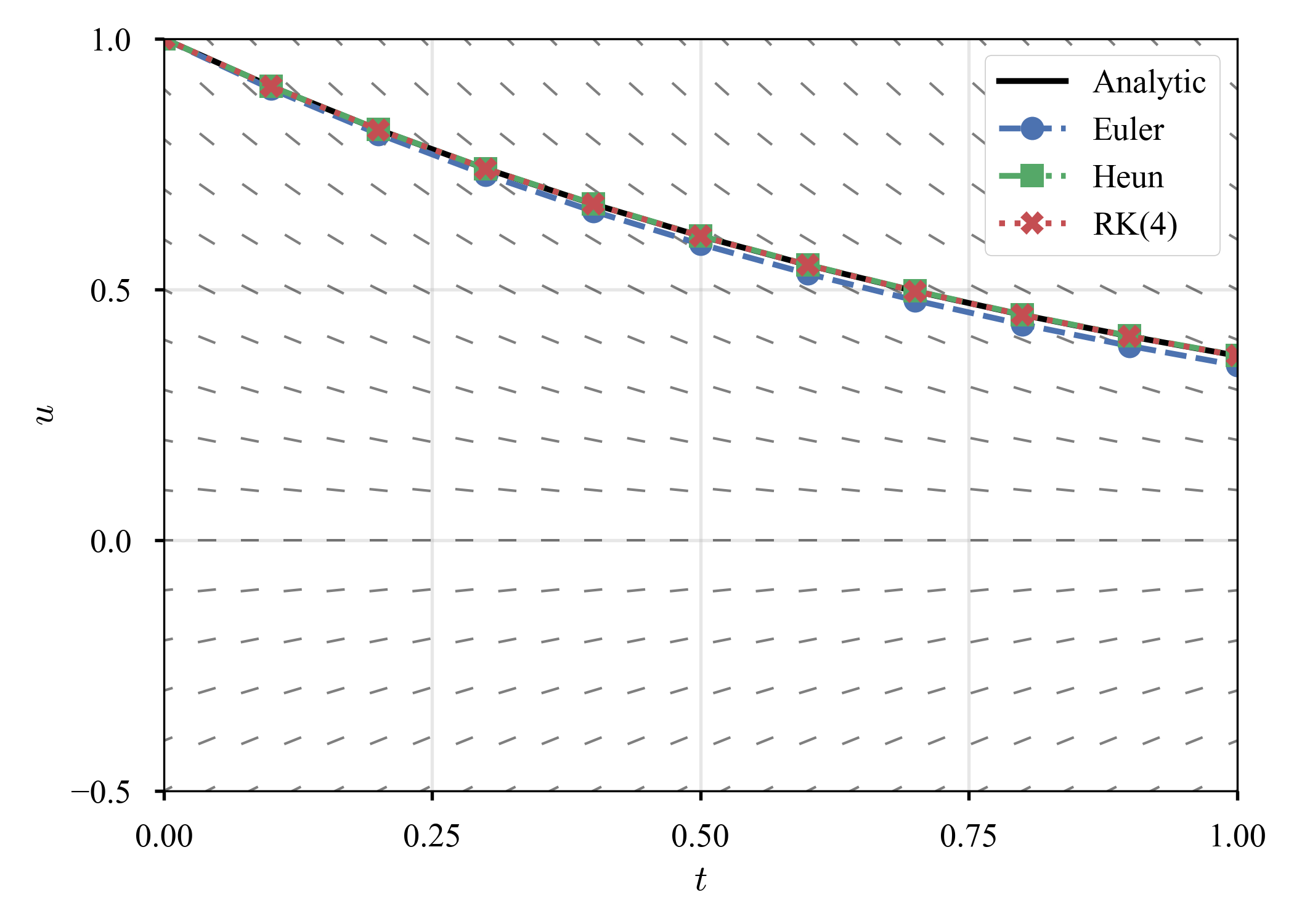 |
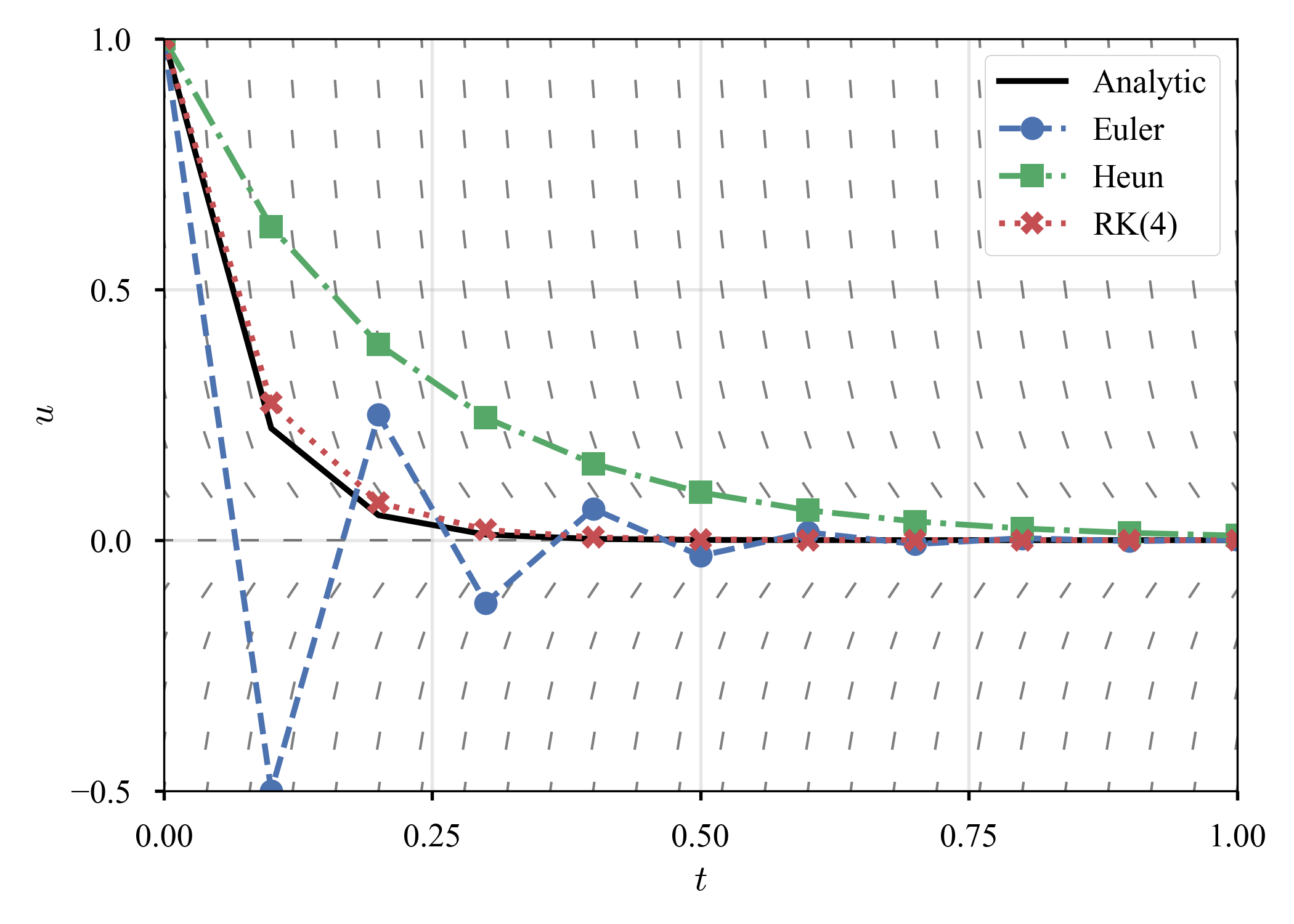 |
同じ時間増分で,殆ど同じ問題を解いているのに,精度には大きな違いがある.もう少し,他の硬い方程式も見てみよう.
Curtiss and Hirschfelder (1952) の例
\begin{align}
\frac{d}{d t} u \left( t \right)
&= - 50 \left( u - \cos \left( t \right) \right) \\
u \left( 0 \right)
&= 0 \\
\end{align}
を見る.解曲線と,異なる時間増分での結果を示す.
| 勾配場 | $\tau = 0.04$ | $\tau = 0.03$ | $\tau = 0.02$ |
|---|---|---|---|
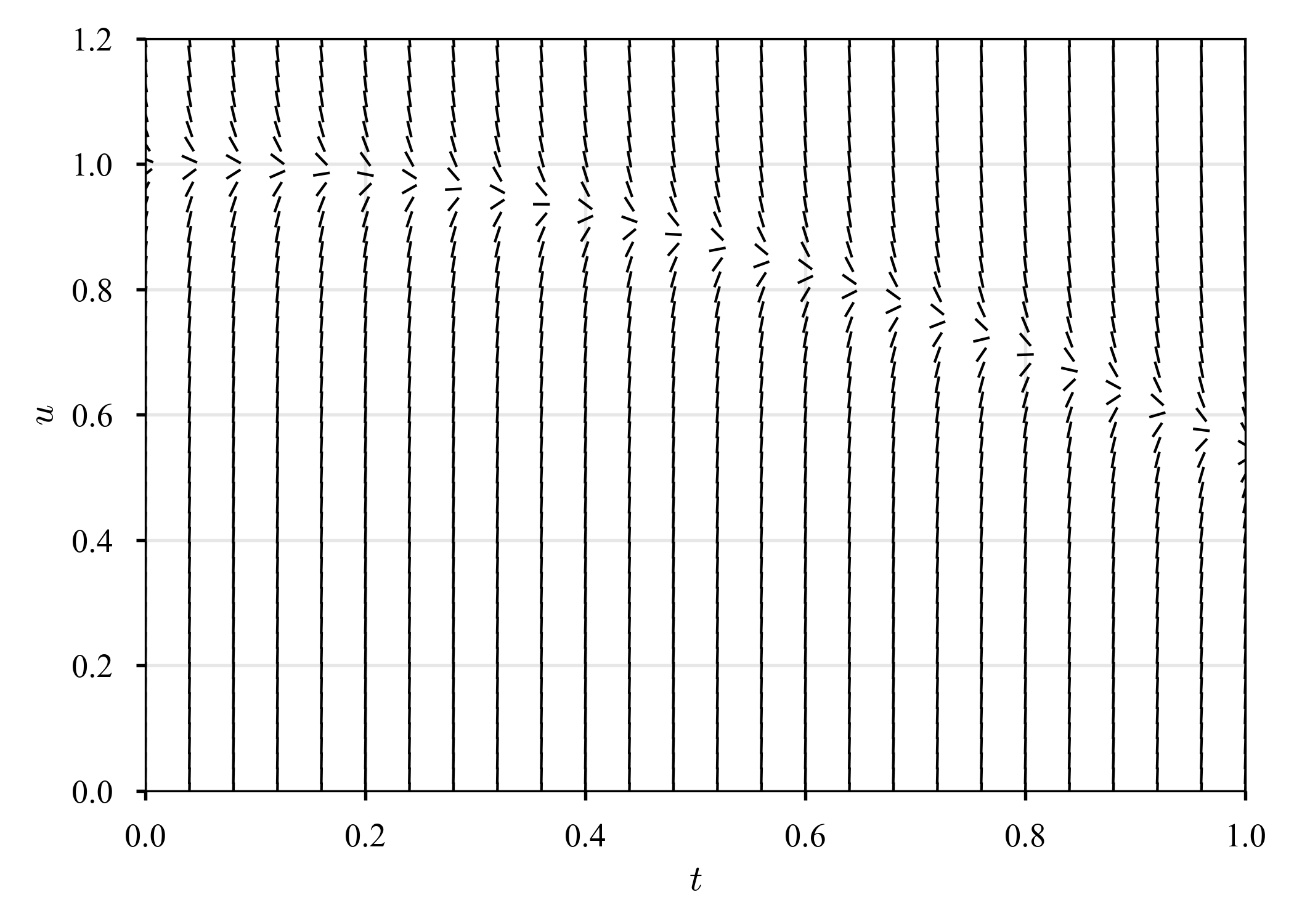 |
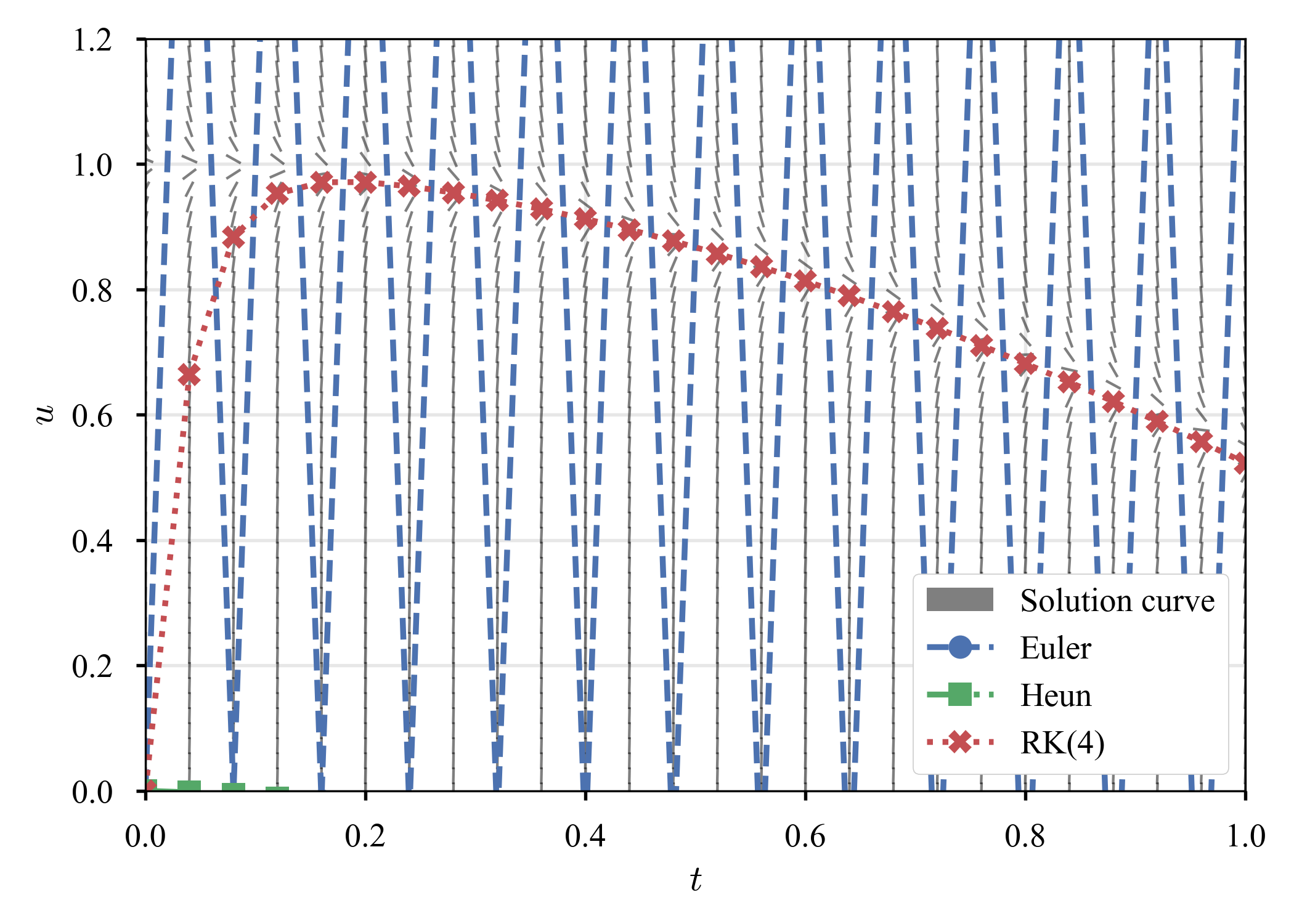 |
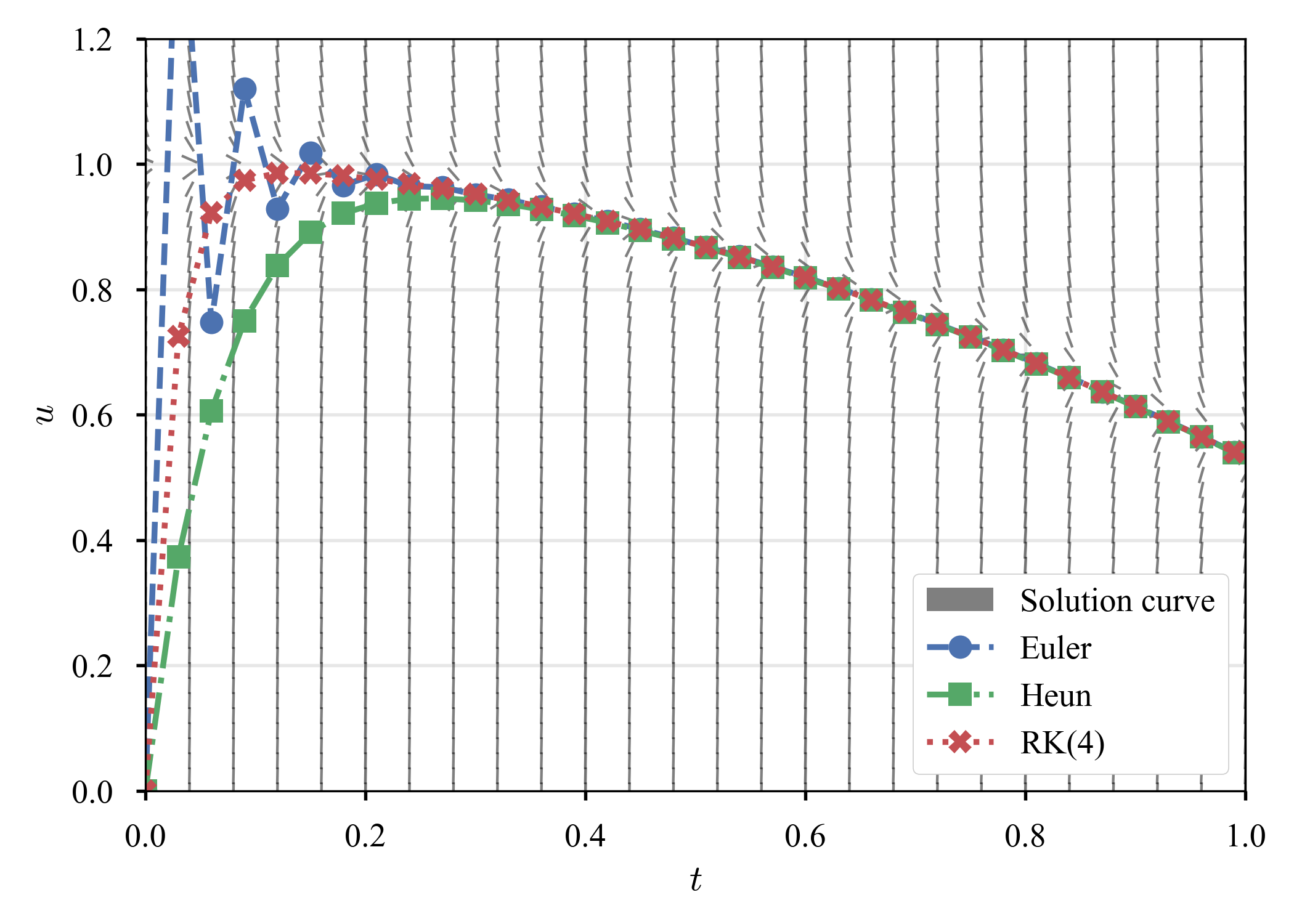 |
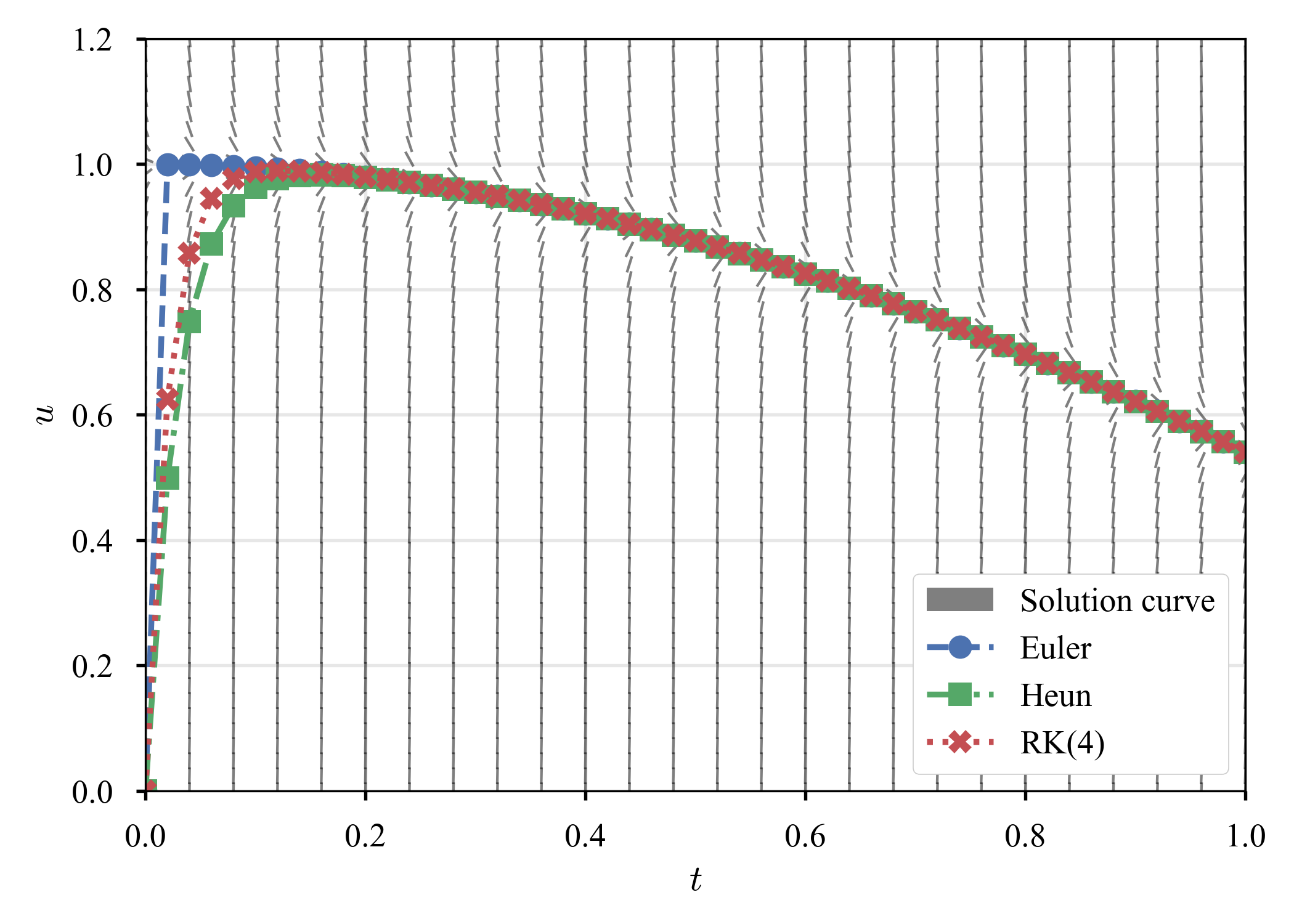 |
勾配場(解曲線)を見ると,ある滑らかな解($u \simeq \cos (t)$)があるようだが,その他のあらゆる解は急速な過渡期を経て,その解に近づいている.このような現象は,硬い方程式によく見られる($\dot{u} = - 15 u$でも見た).ただし,過渡期の存在は,その方程式がstiffであるための十分条件でも,必要条件でもないことに注意しなければならない.実際,初期値に$u \left( 0 \right) = 2500 / 2501 \simeq 1$を選べば,このような振動は発生しない(元の方程式は安定).
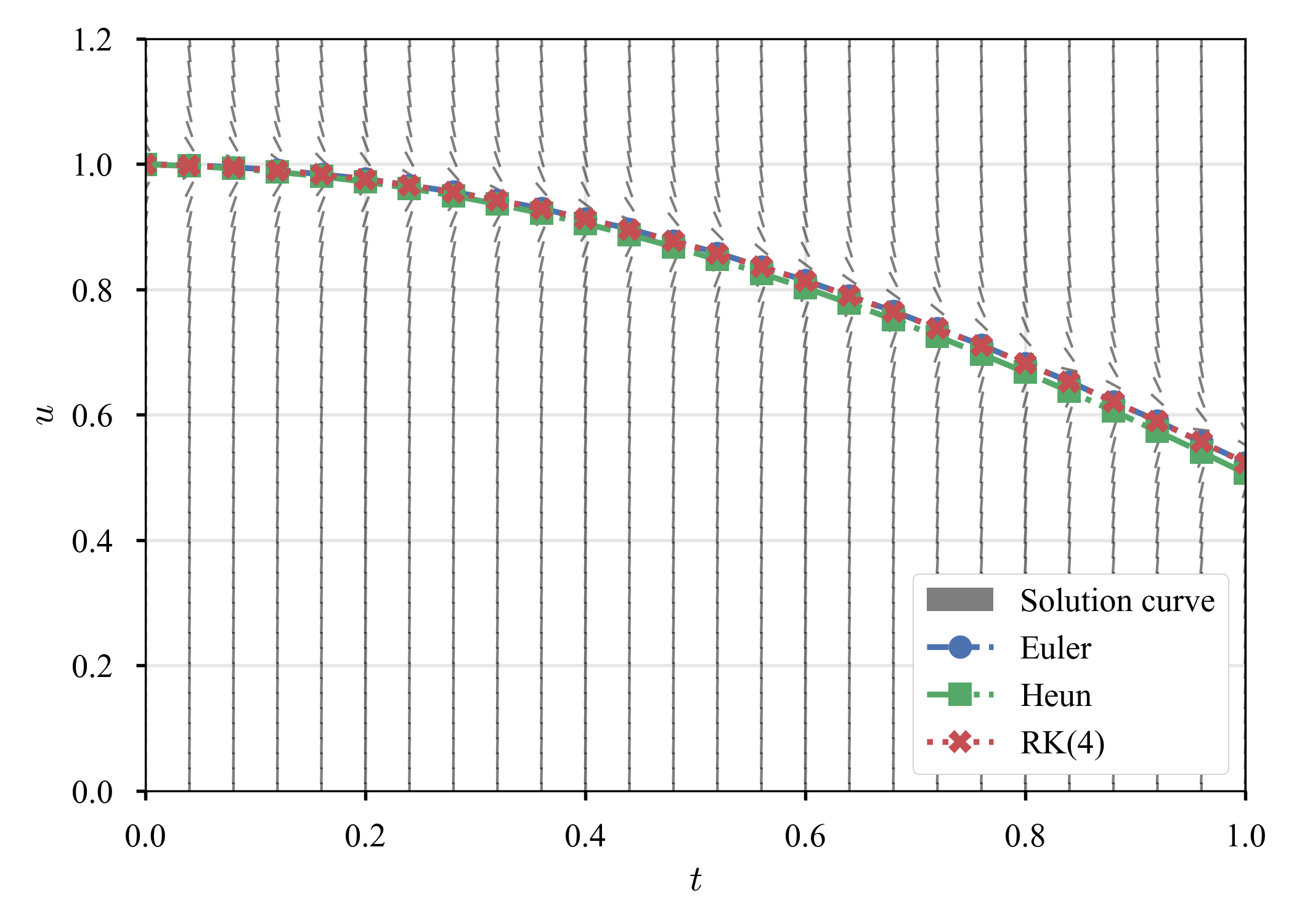
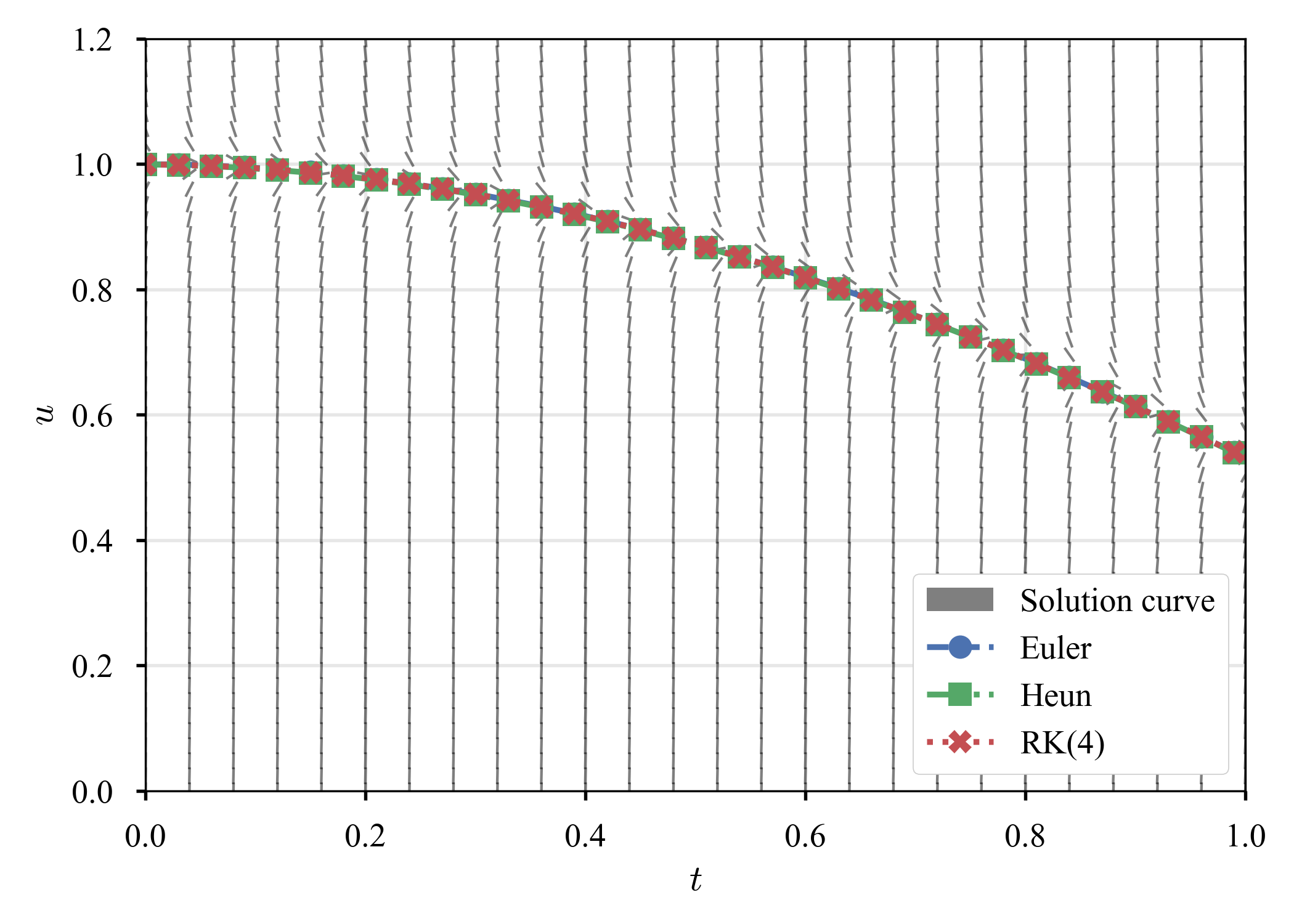
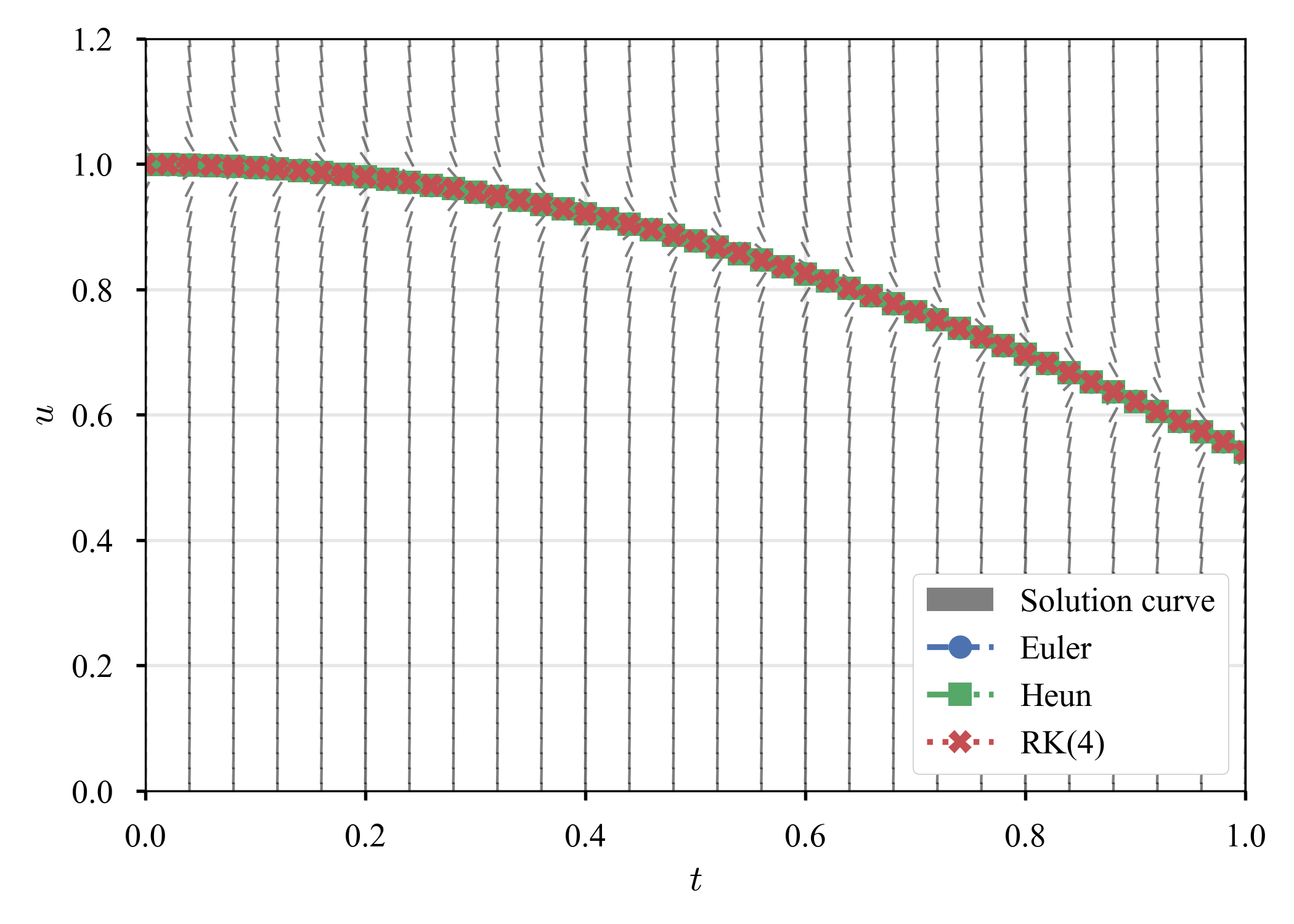
| 勾配場 | $\tau = 0.04$ | $\tau = 0.03$ | $\tau = 0.02$ |
|---|---|---|---|
 |
 |
 |
 |
これ以上は深淵にハマりそうなので,解曲線を7年ぶりに描いて満足したし,足を洗っておく.取り敢えず,stiffnessというものに触れたのがtakeawayである.
熱放射
RK(2, 2)系の方法について,彼らのコードが正しく書けたか確認するため,こちらを参考に,
\begin{align}
\frac{du}{dt}
&= - 2.2067 \times 10^{-12}
\left(
u^{4} - 8.1 \times 10^{9}
\right) \\
u
&= 1.2 \times 10^{3}
\end{align}
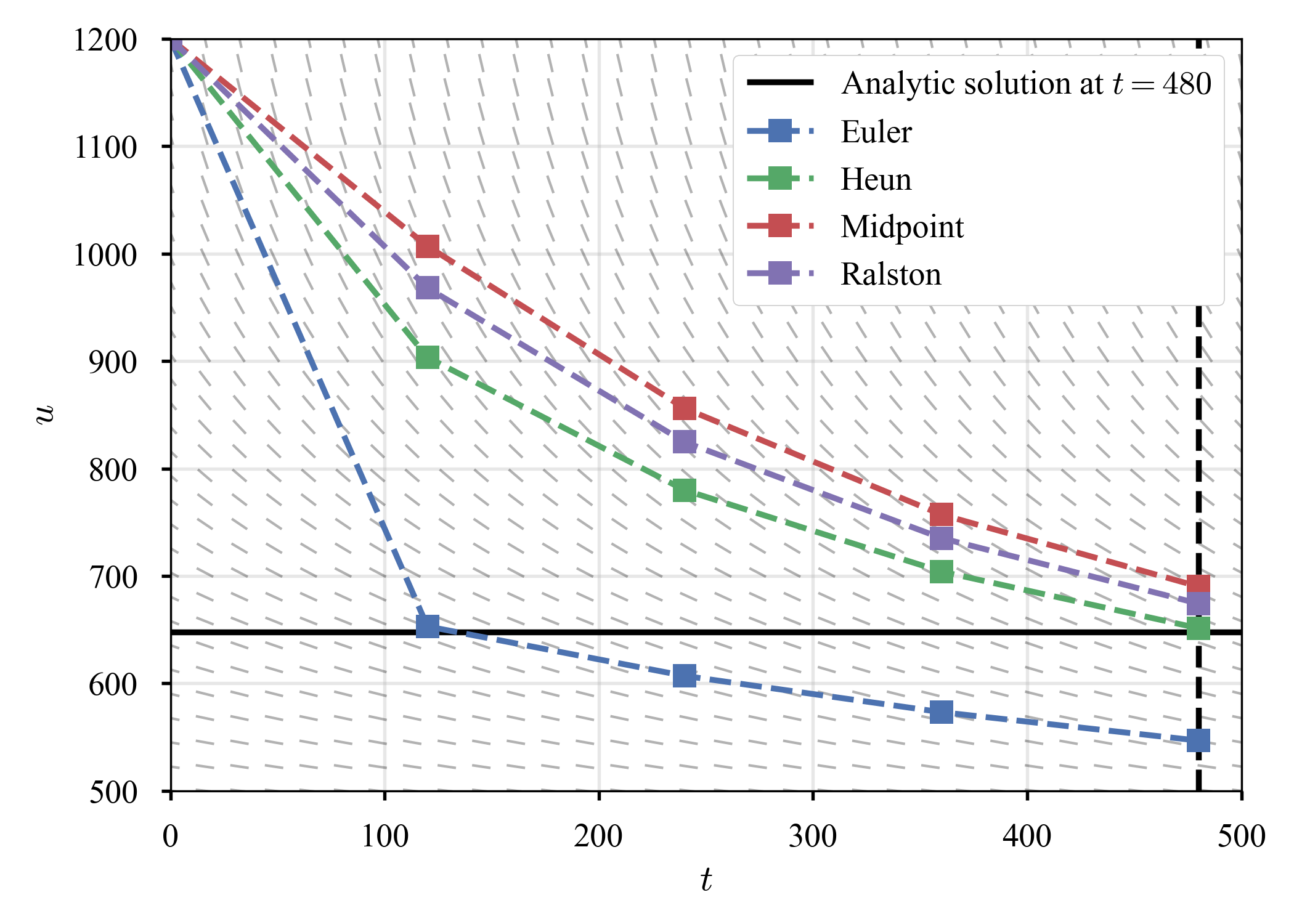
を考える.$1,200 [\mathrm{K}]$に熱された質点が外気に晒され,クールダウンする(Newtonの冷却の法則かと思いきや,少し違う).厳密解は$u (t = 480) = 647.57 [\mathrm{K}]$(厳密解をどうやって得るか良く理解できないので,取り敢えず,この時刻だけ見る.).
| 比較 | 誤差(1) | 誤差(2) |
|---|---|---|
 |
 |
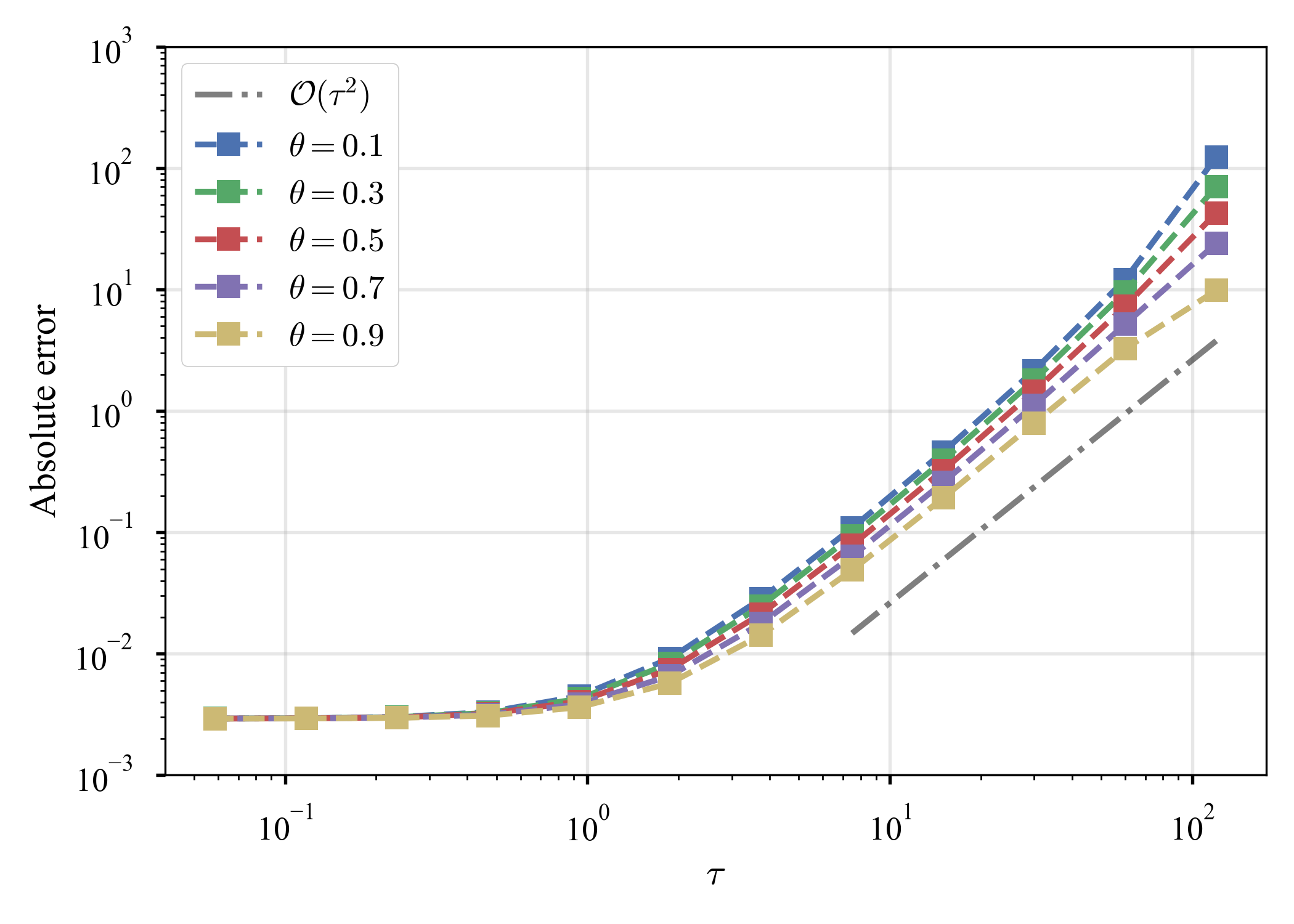 |
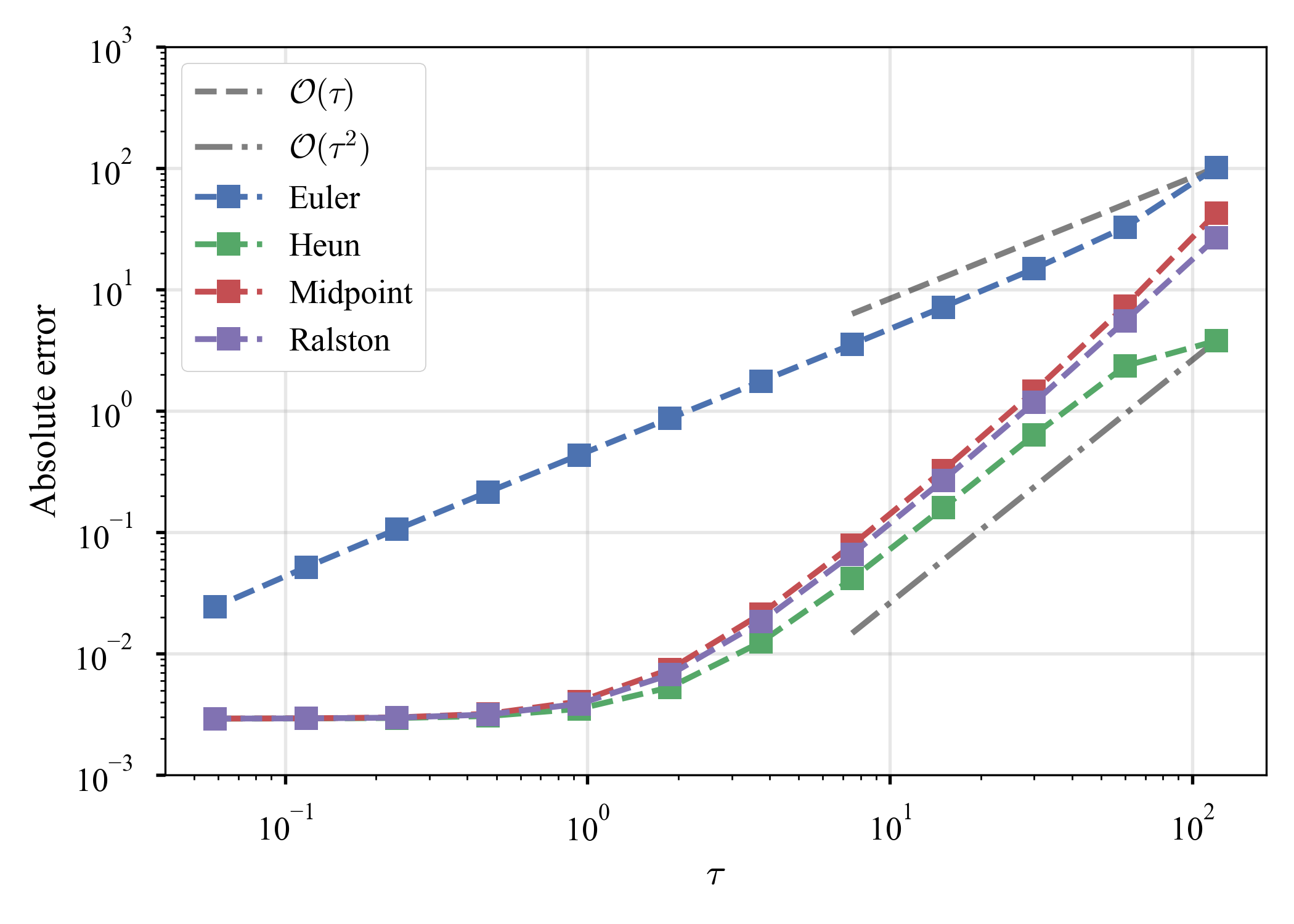
比較の図が,参考にしたサイトと凡そ合致するので,正しくコードが書けたと思う.また,誤差(1)の図から,Heun法,中点法,Ralston法が2次の速度を持っていることが分かる.誤差(2)の図から,$\theta$を適当に動かしても2次の速度が出るようだが,そんな変なことをする論文は見たことが無いね.
成長曲線
Logistic curve
ある生物の個体数がcarrying capに到達するまで増加する5.
\begin{align}
\frac{dP}{dt}
&= r P \left( 1 - \frac{P}{K} \right)
\end{align}
ここで,$P$は生物の個体数(population),$r$は増加率,$K$はcarrying capacityである.成長に制限がないとき($K \to \infty$),Malthusの指数増加モデルに一致する.
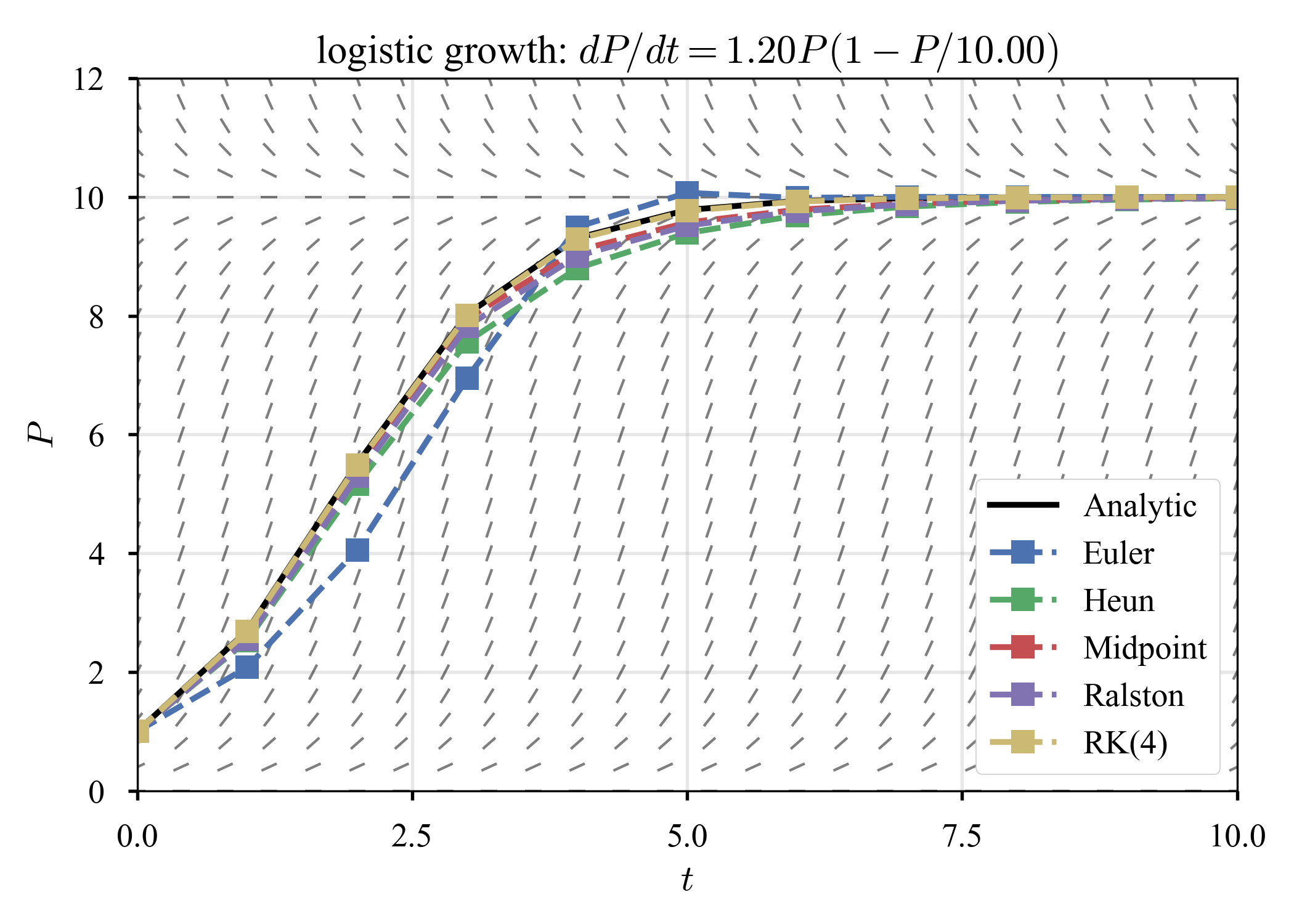
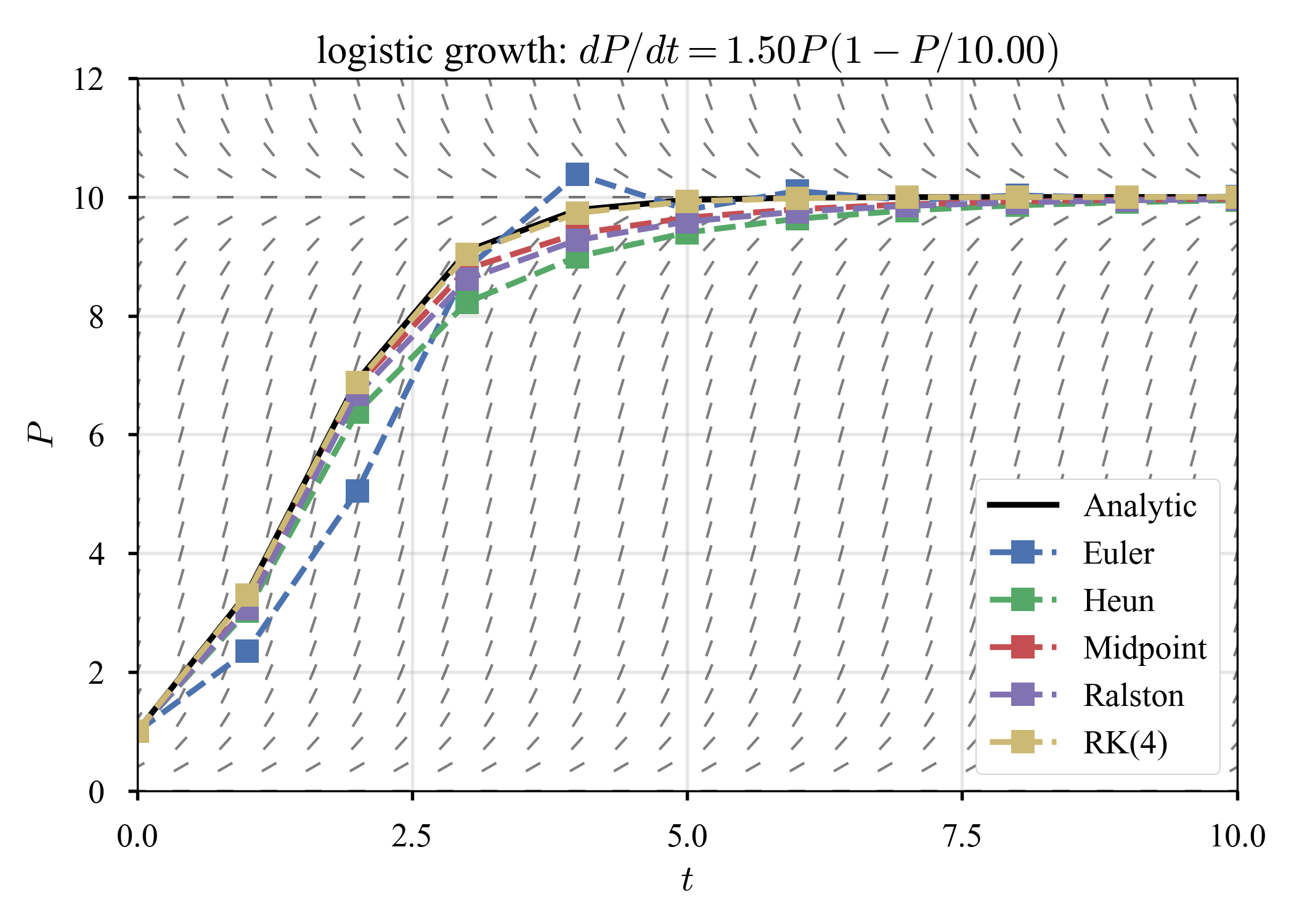
$K = 10, \tau = 1, T = 10$に固定して,成長率だけ変化させる.
| $r = 1.2$ | $r = 1.5$ | $r = 1.8$ |
|---|---|---|
 |
 |
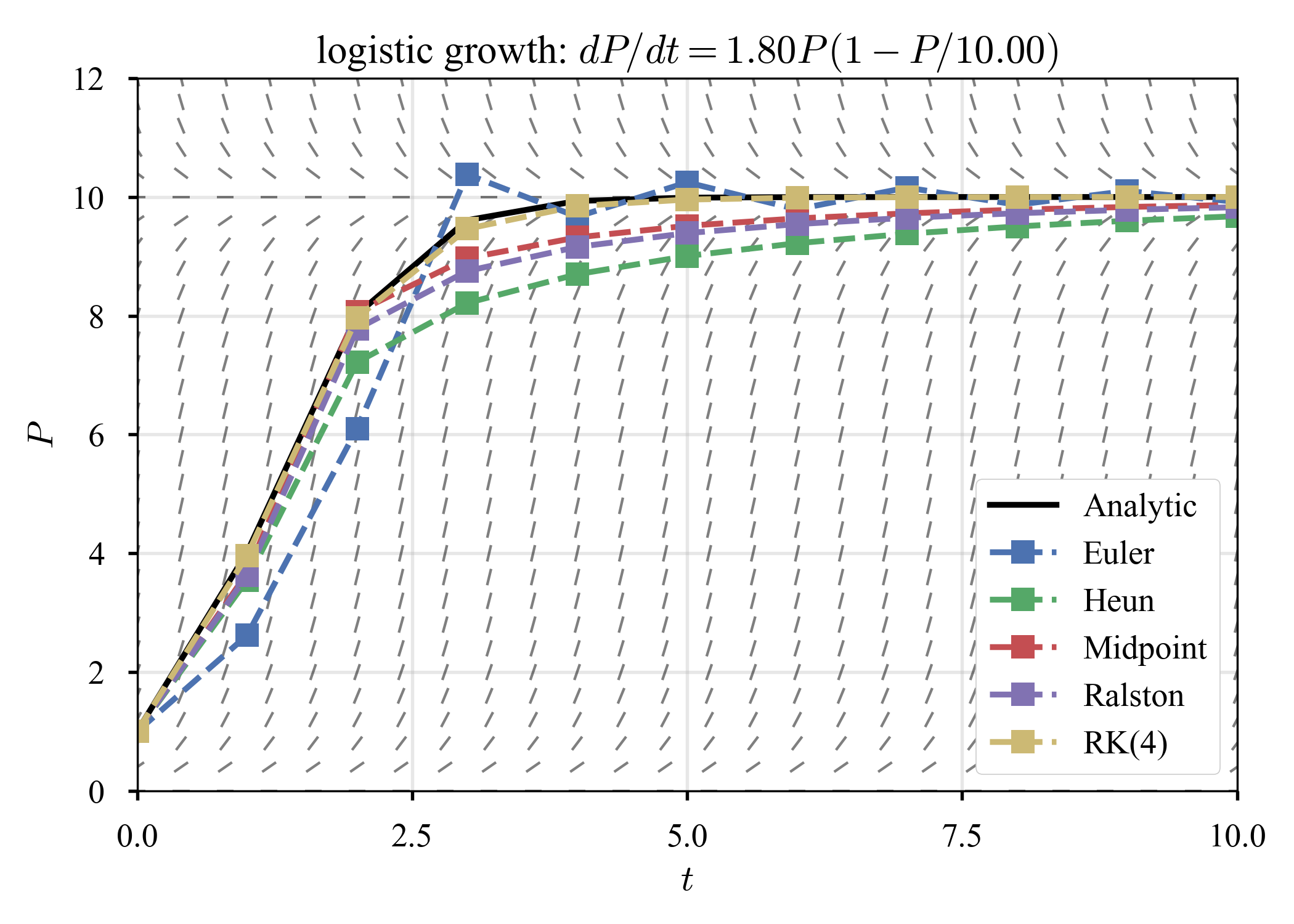 |
$K$から離れた場所からスタートすると,$r$の増加に伴い,系は硬い?(少なくとも,素早い過渡期の存在).
Gompertz curve
成長曲線の一つ6.
\begin{align}
\frac{dP}{dt}
&= r P \ln \left( \frac{K}{P} \right)
\end{align}
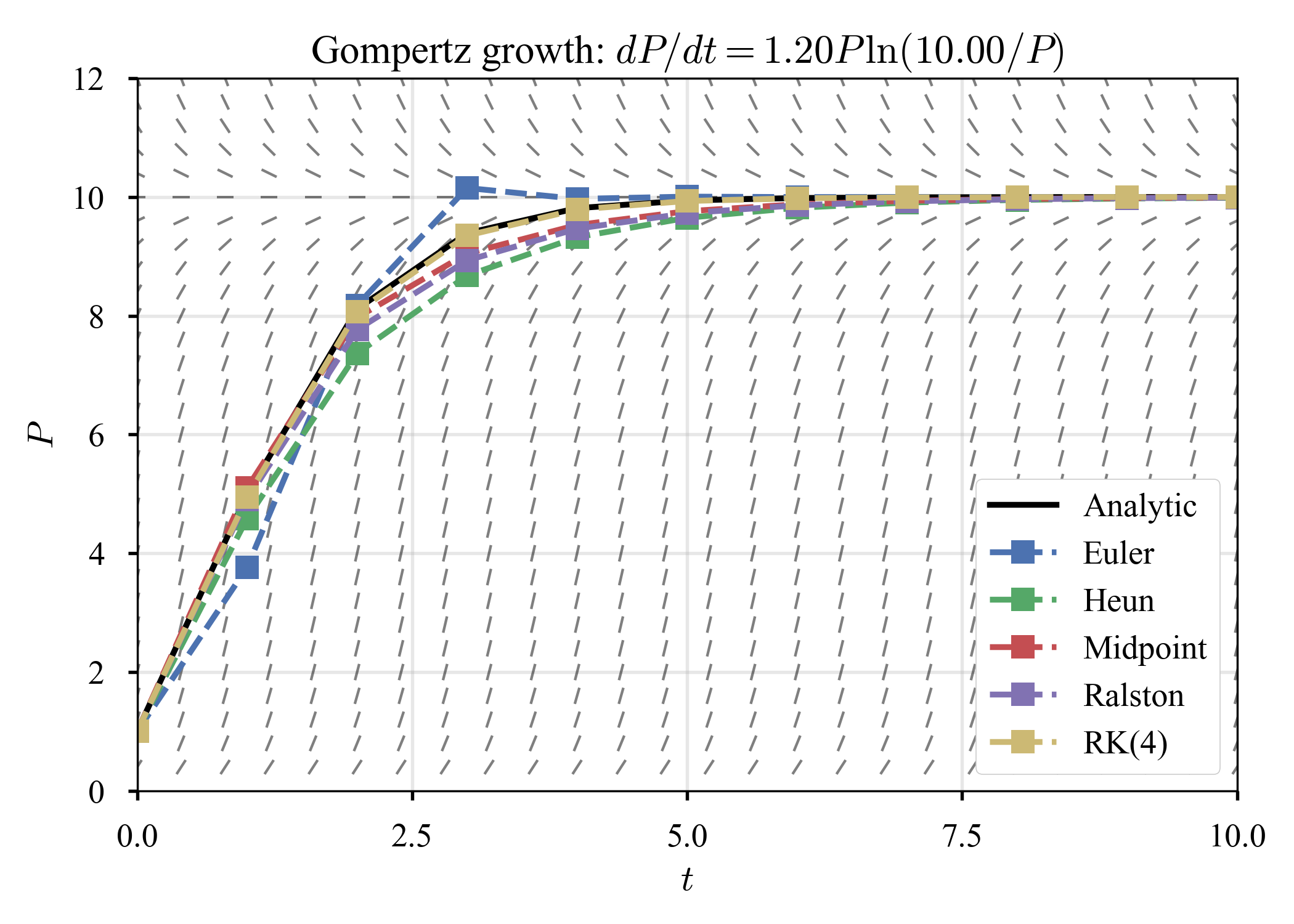
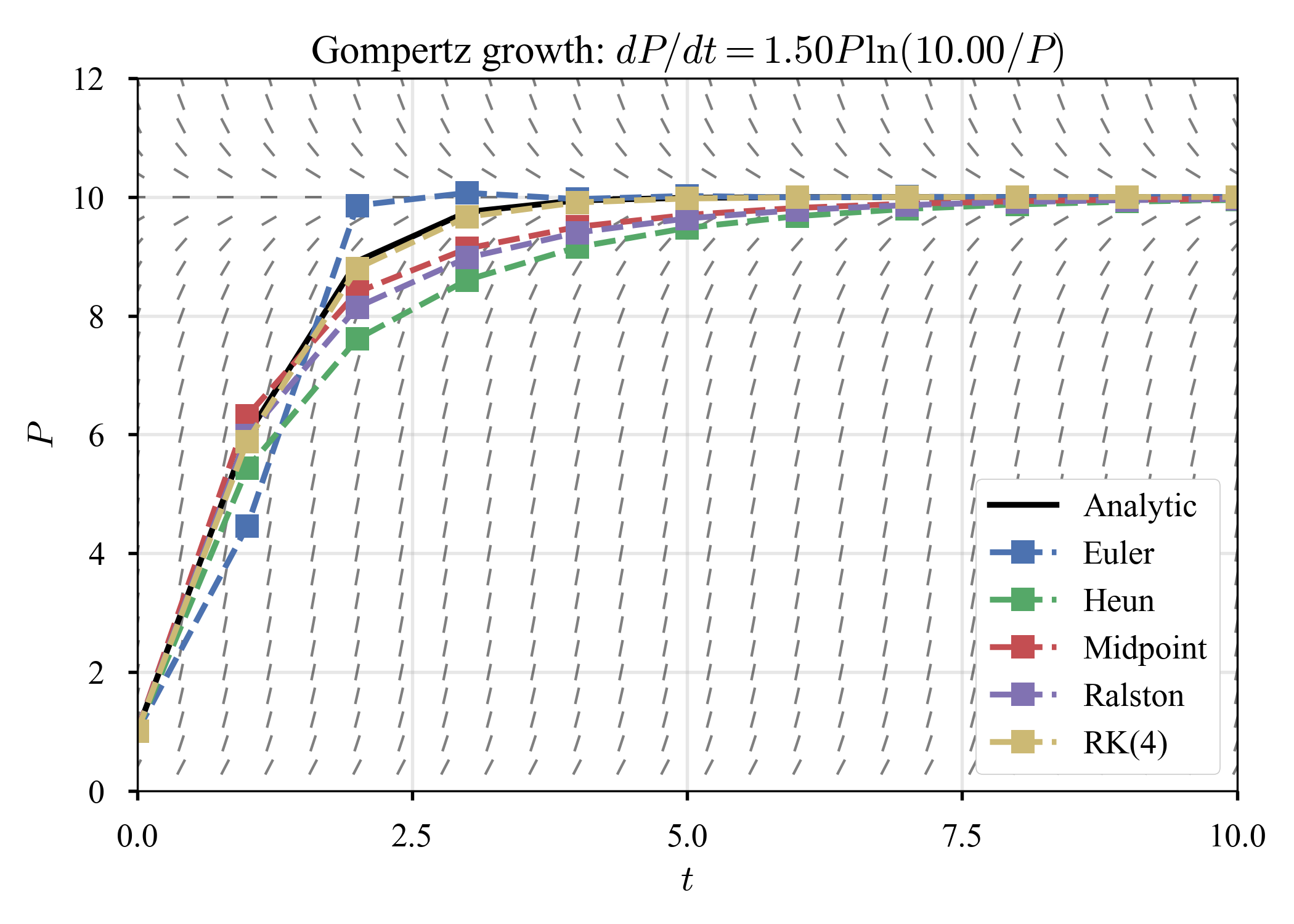
$K = 10, \tau = 1, T = 10$に固定して,成長率だけ変化させる.
| $r = 1.2$ | $r = 1.5$ | $r = 1.8$ |
|---|---|---|
 |
 |
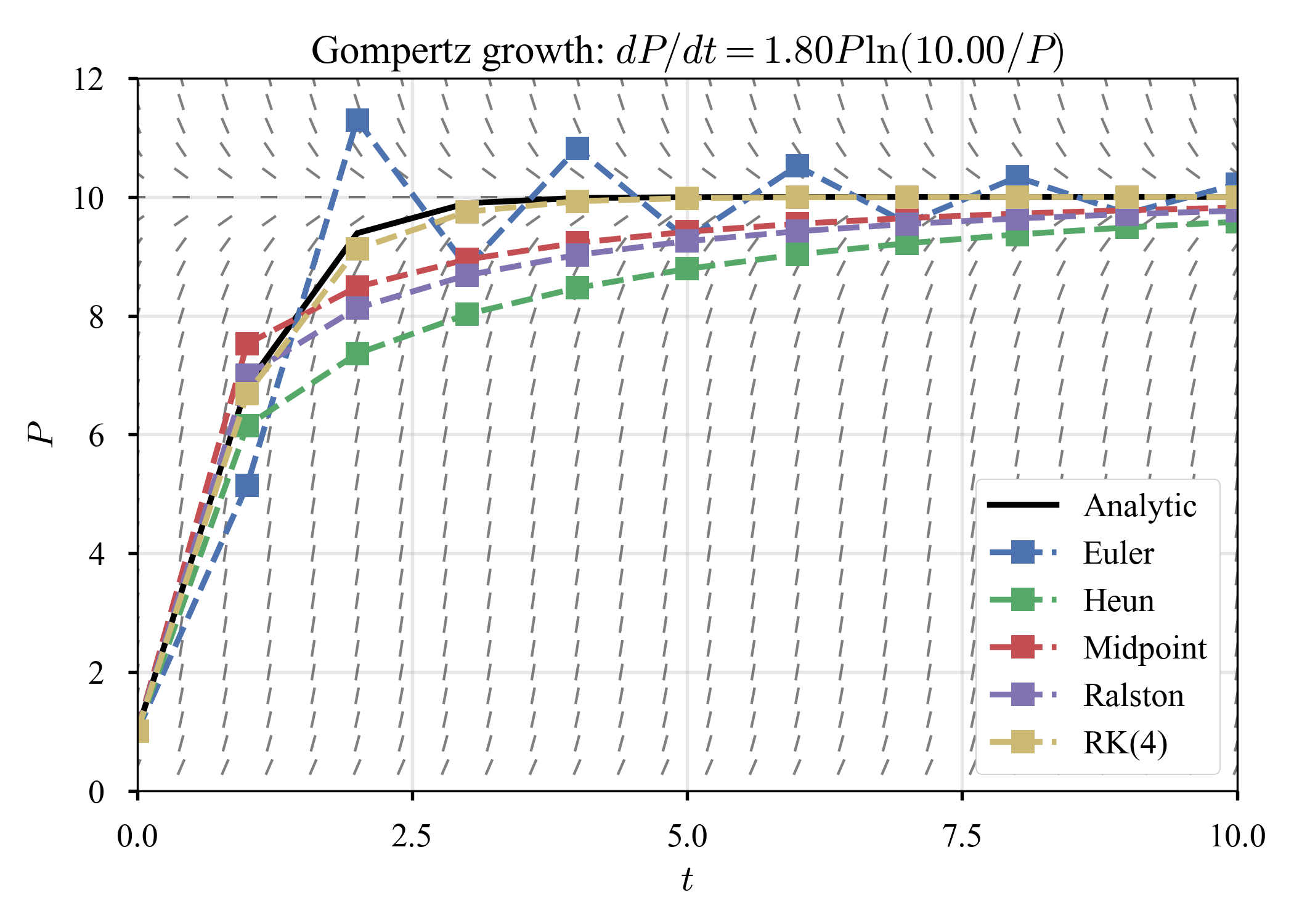 |
開発上のバグの個数を数えていき,Gompertz curveに当てはめ,頭打ちになるところを推定すれば,プログラム中に残されているバグの個数が見積もれるらしい(cf. こちら).
Lotka–Volterra system
捕食者(predator)と被食者(prey)の個体数の推移を記述する.
\begin{align}
&\begin{cases}
\dot{p}_1
= \alpha p_1 - \beta p_1 p_2 \\
\dot{p}_2
= \delta p_1 p_2 - \gamma p_2 \\
\end{cases} \\
\end{align}
$p_1$は被食者(prey)の個体数密度,$p_2$は捕食者(predator)の個体数密度.パラメータと初期値を
- Case 1: $\left( \alpha, \beta, \delta, \gamma \right) = \left( 2/3, 4/3, 1, 1 \right)$,$\left( p_1 (t=0), p_2 (t=0) \right) = \left( 1, 1 \right)$
- Case 2: $\left( \alpha, \beta, \delta, \gamma \right) = \left( 1.5, 1, 1, 3 \right)$,$\left( p_1 (t=0), p_2 (t=0) \right) = \left( 10, 5 \right)$
- Case 2: $\left( \alpha, \beta, \delta, \gamma \right) = \left( 2, 1, 1, 1 \right)$,$\left( p_1 (t=0), p_2 (t=0) \right) = \left( 2, 2 \right)$
に定めて解いてみる($\tau = 10^{-2}$).
| # | Population | Phase |
|---|---|---|
| 1 | 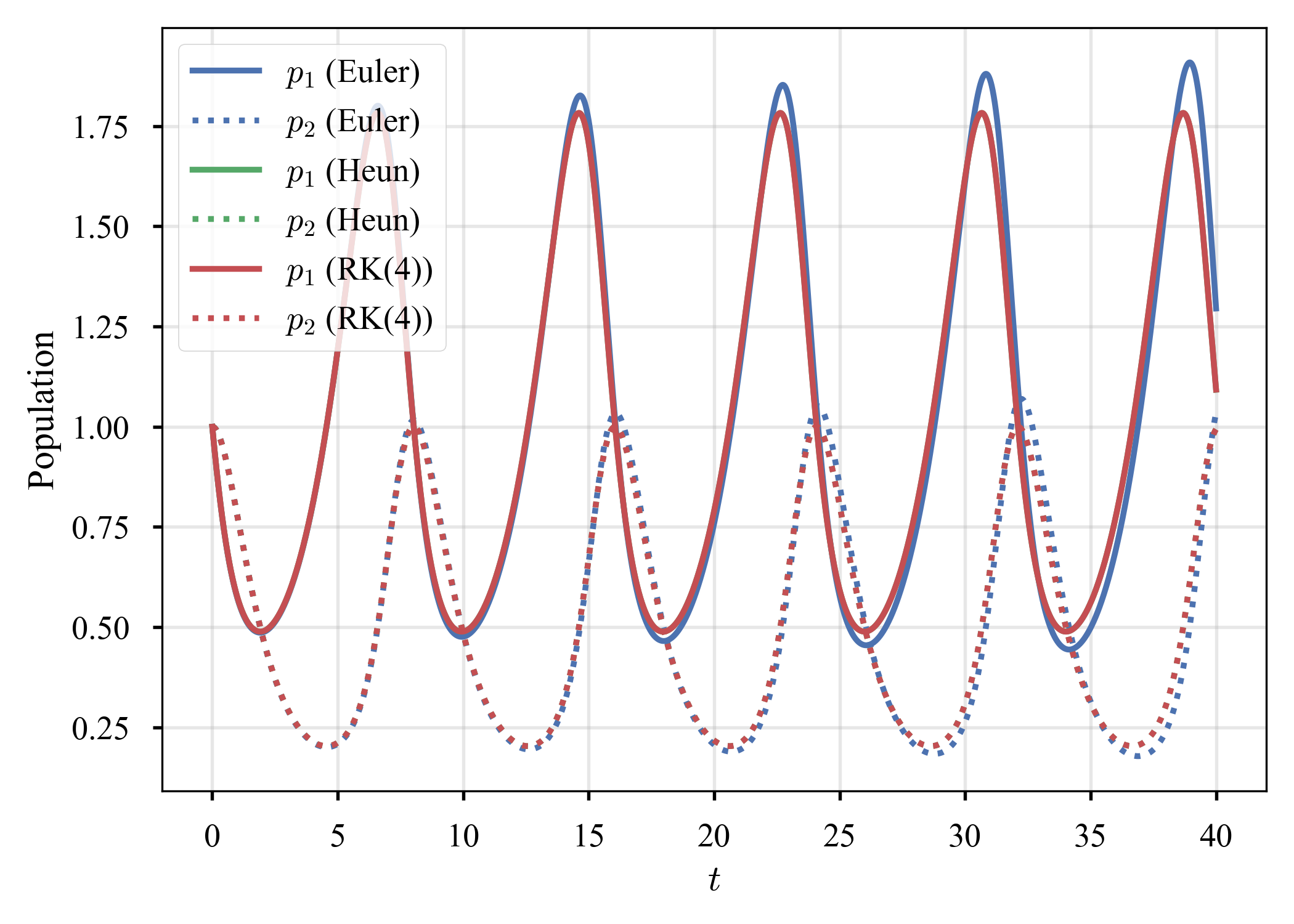 |
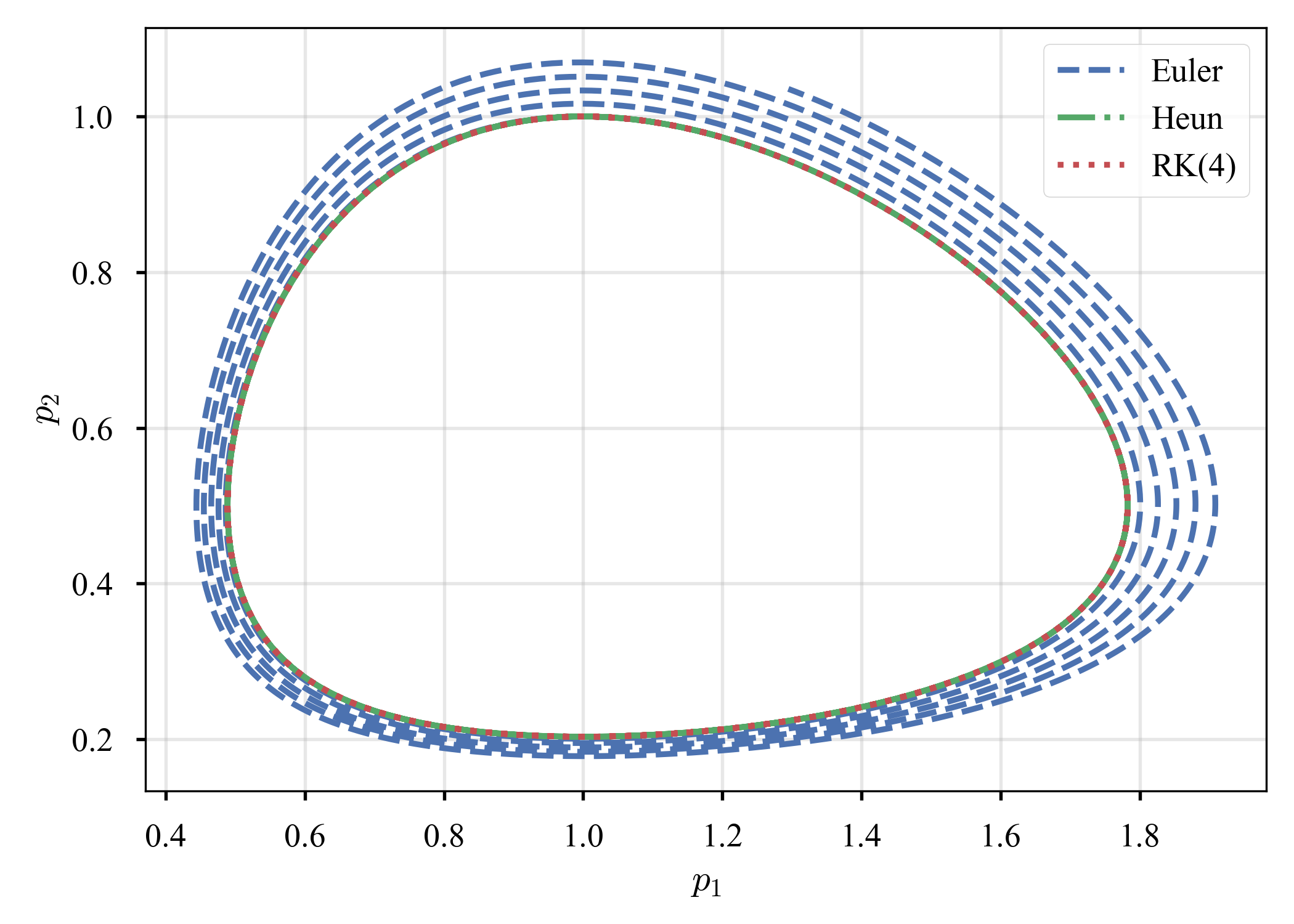 |
| 2 | 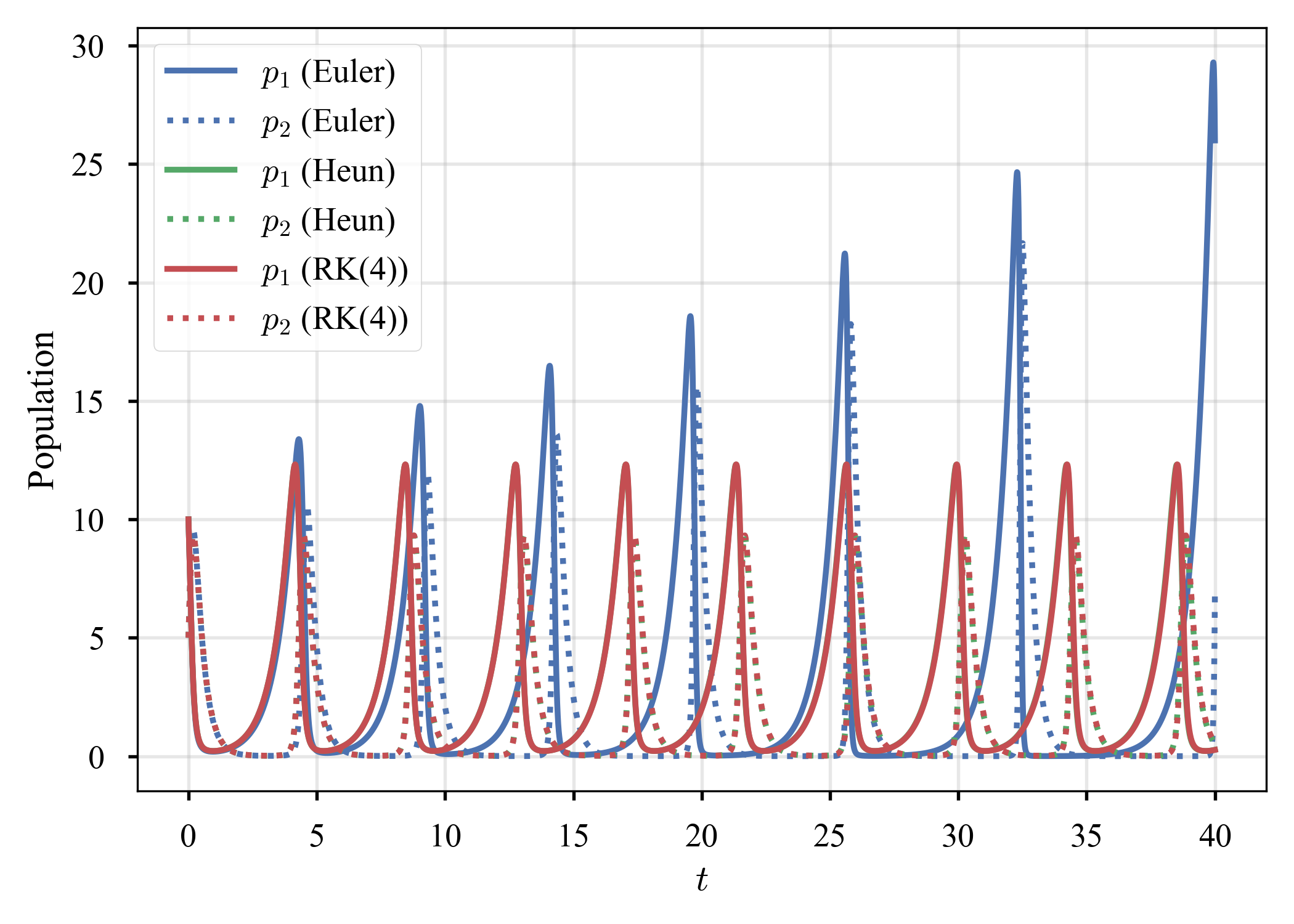 |
 |
| 3 | 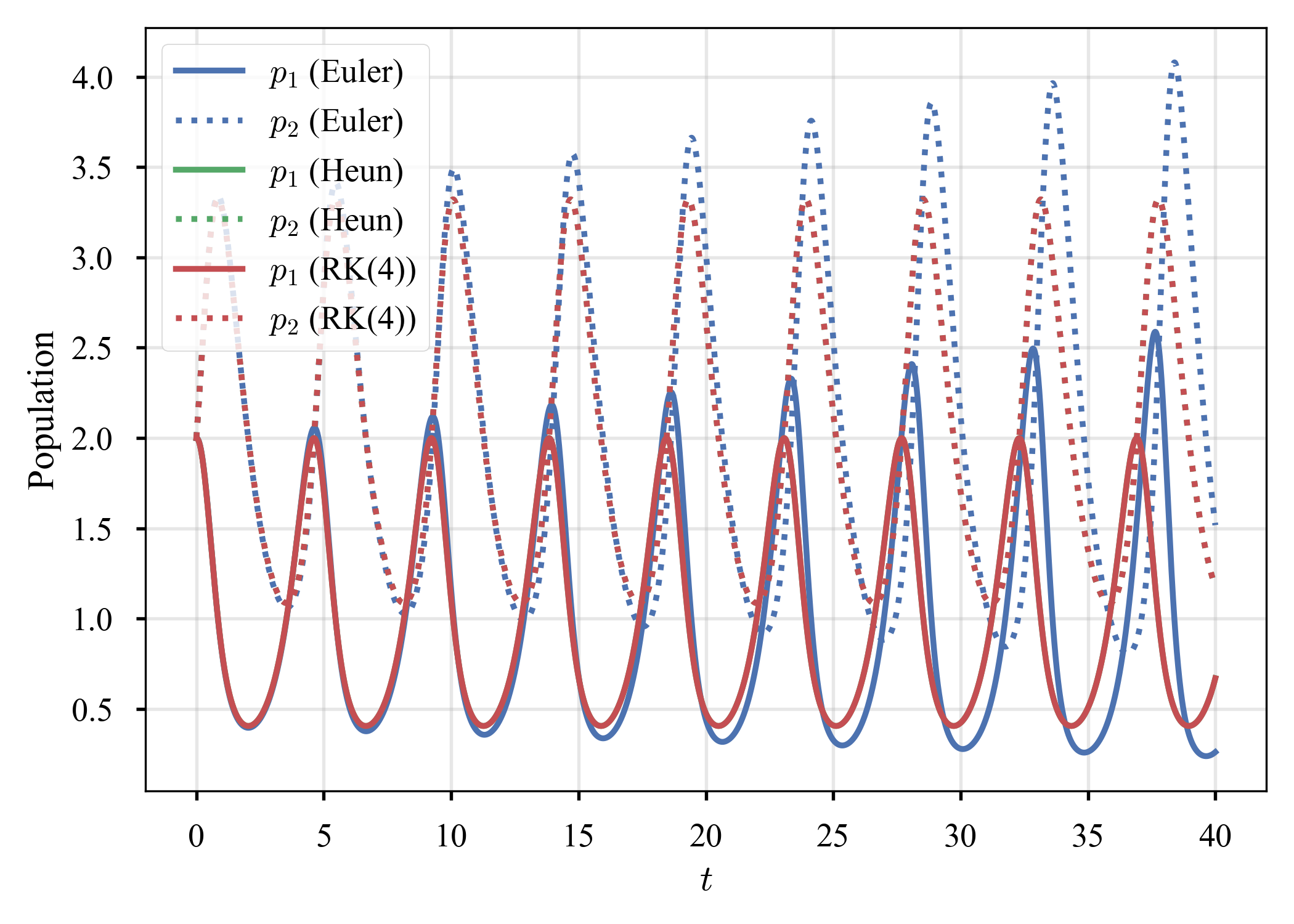 |
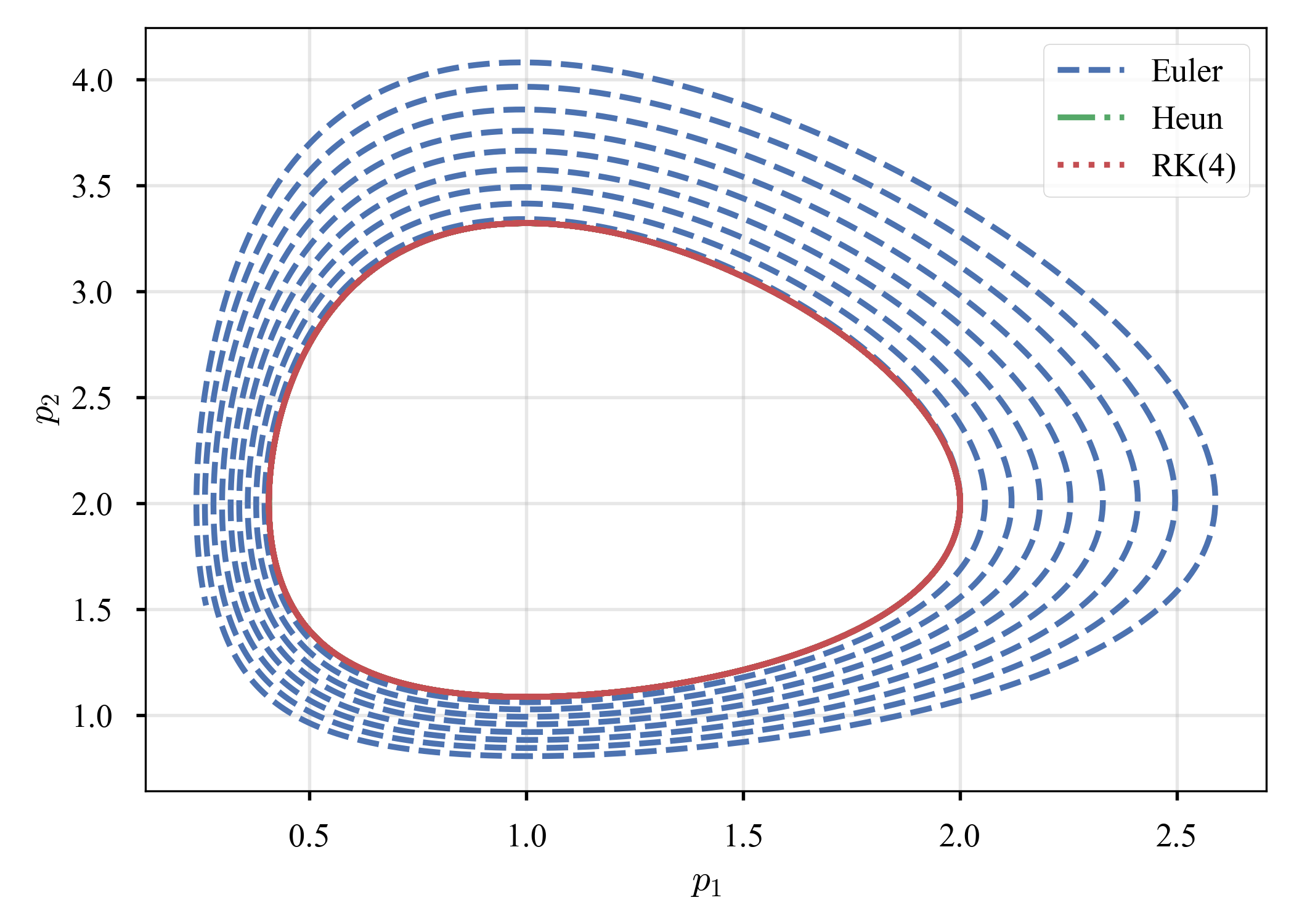 |
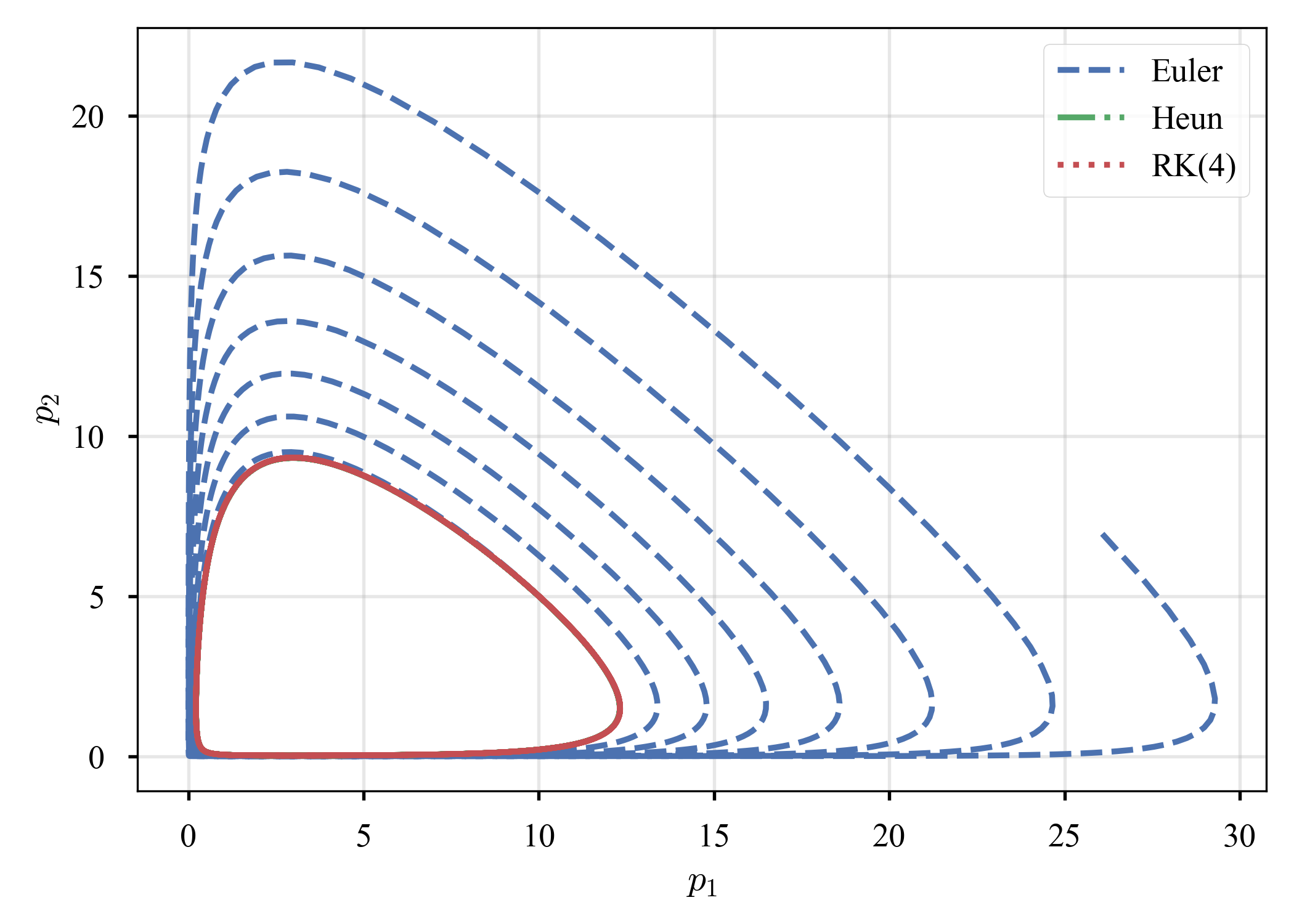
Euler法だけ,上下のピークが増大し,phaseが閉じていない(Euler法では閉じないのが正解か? cf. ここやここ).相空間から,何らかの形でシンプレクティックな方法との関連を感じるが,未だ良く分かっていない.シンプレクティック法の勉強をしてから振り返ってみようと思う(宿題にする).
Lorenz63
余りに有名(Lorenz1963).カオス的振舞いを目にしたいだけという,何とも安直な発想.
\begin{align}
\dot{x}_1
&= \sigma \left( x_2 - x_1 \right) \\
\dot{x}_2
&= x_1 \left( \rho - x_3 \right) - x_2 \\
\dot{x}_3
&= x_1 x_2 - \beta x_3 \\
\end{align}
$\left( \sigma, \beta, \rho \right) = \left( 10, 8/3, 28 \right)$とする.
初期値の精度による振舞いの違い
所謂,初期値鋭敏性.初期値に差分を与え,同じ問題を,同じ積分法でシミュレートする.
気象学では,「凡そこの辺りだろうか」という初期値を設定し,そこからシミュレーションをスタートしてみる,ということは多いらしい?それがデータ同化などが好まれる理由だろうか?
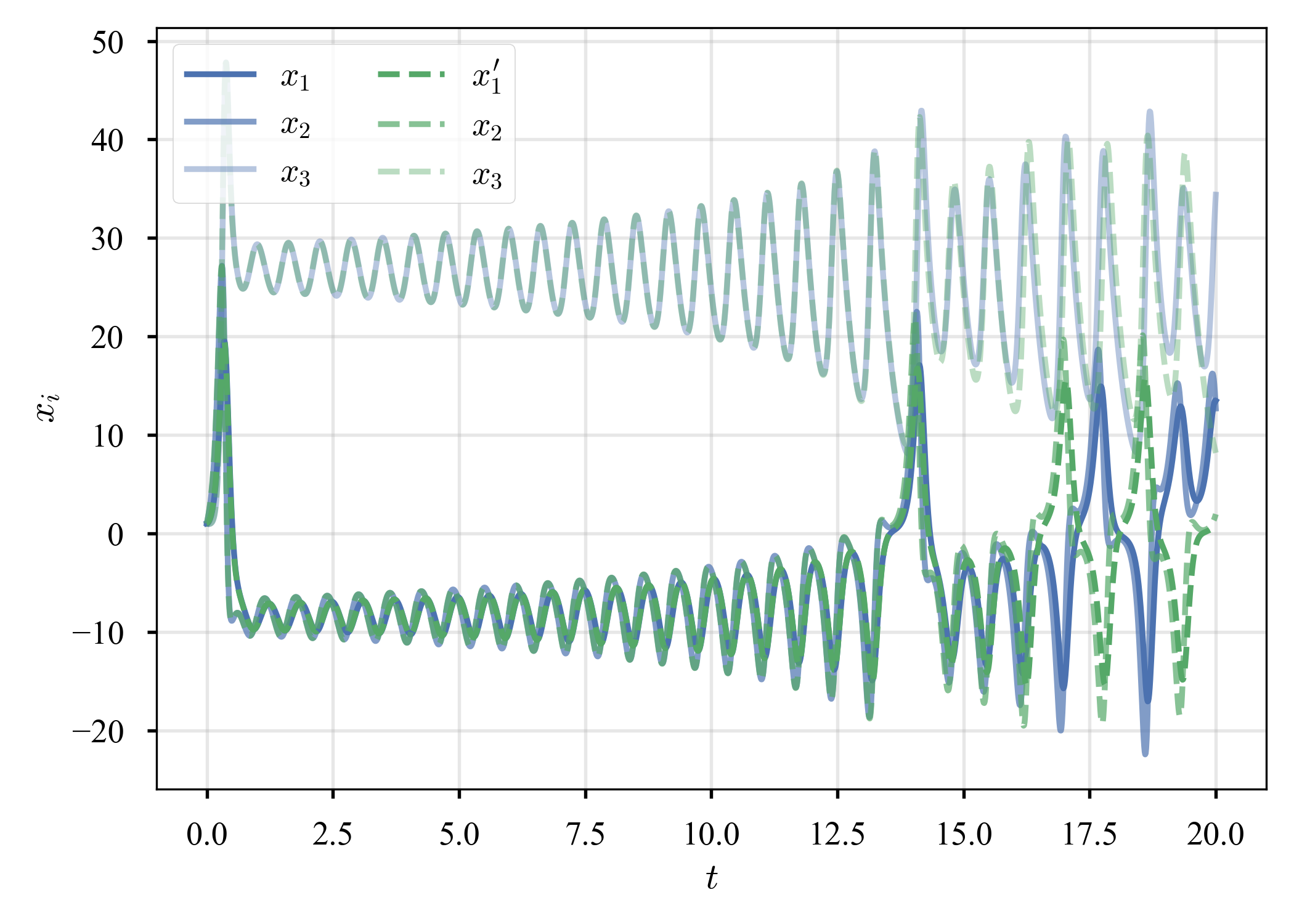
$\left( x_1, x_2, x_3 \right) = \left( 1, 1, 1 \right)$,$\left( x_1, x_2, x_3 \right) = \left( 1.1, 1, 1 \right)$の2つの軌跡を追跡する.
| 2D | 3D |
|---|---|
 |
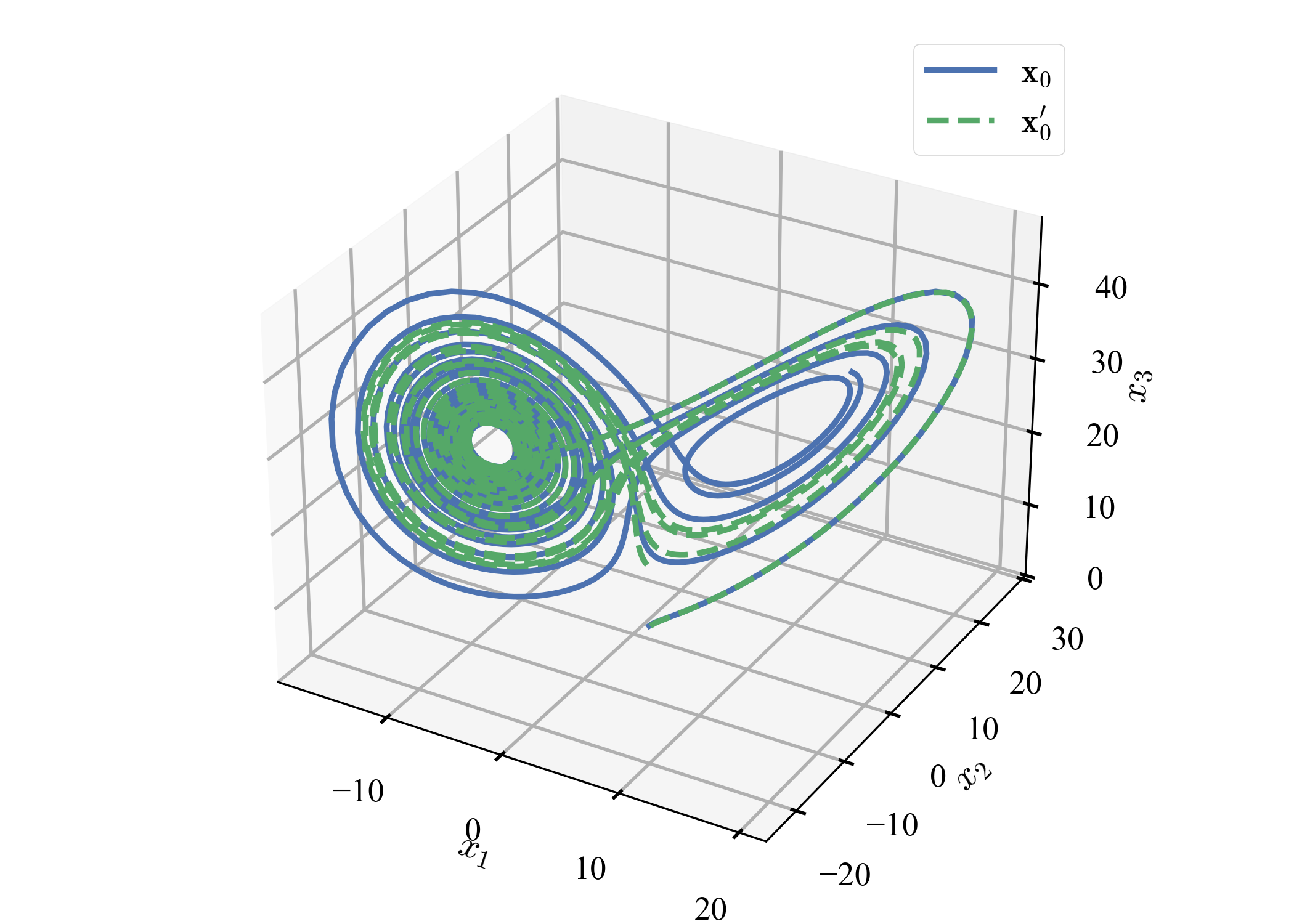 |
15秒くらいから,ズレが顕著になる.
時間増分の違いによる振舞いの違い
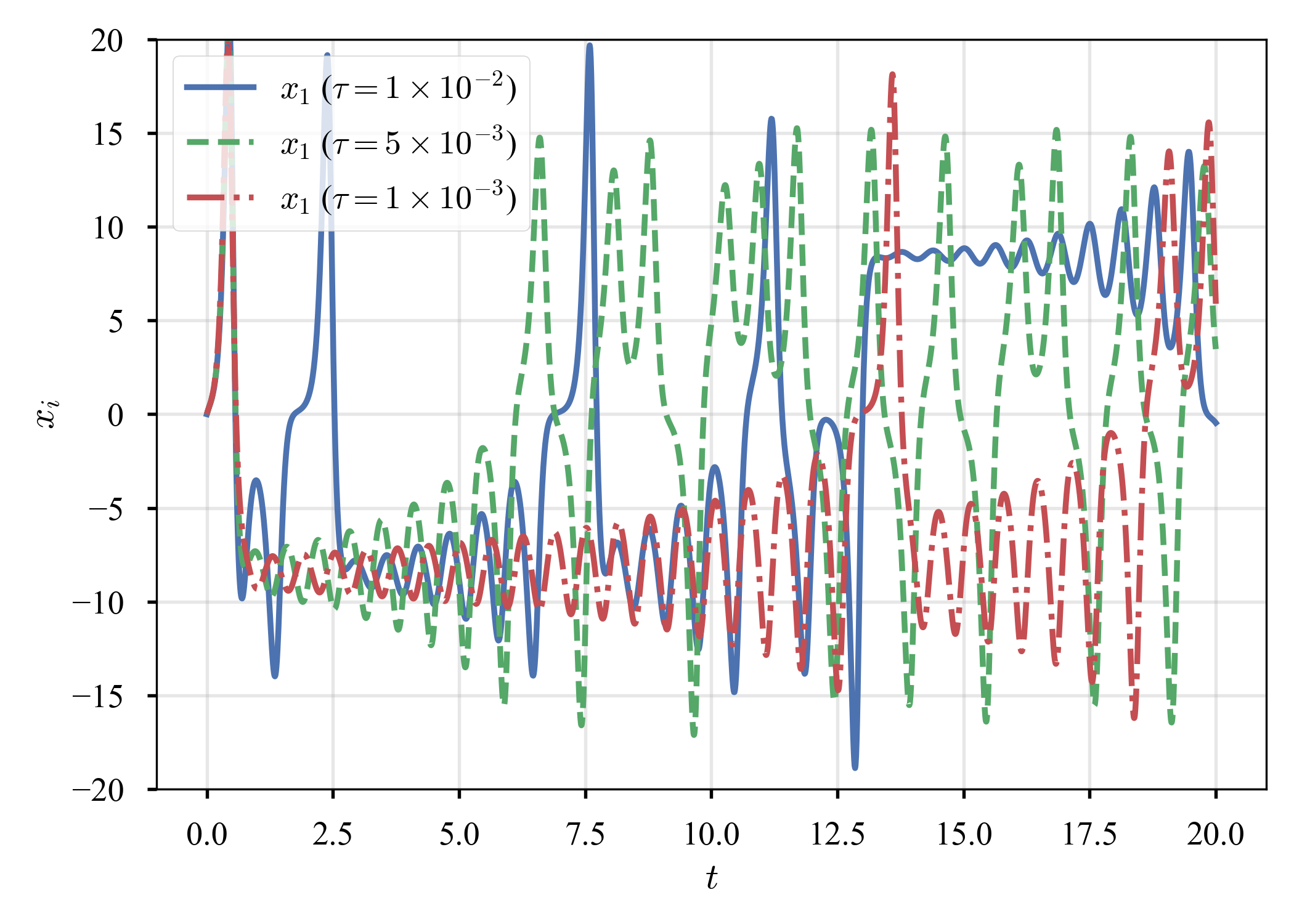
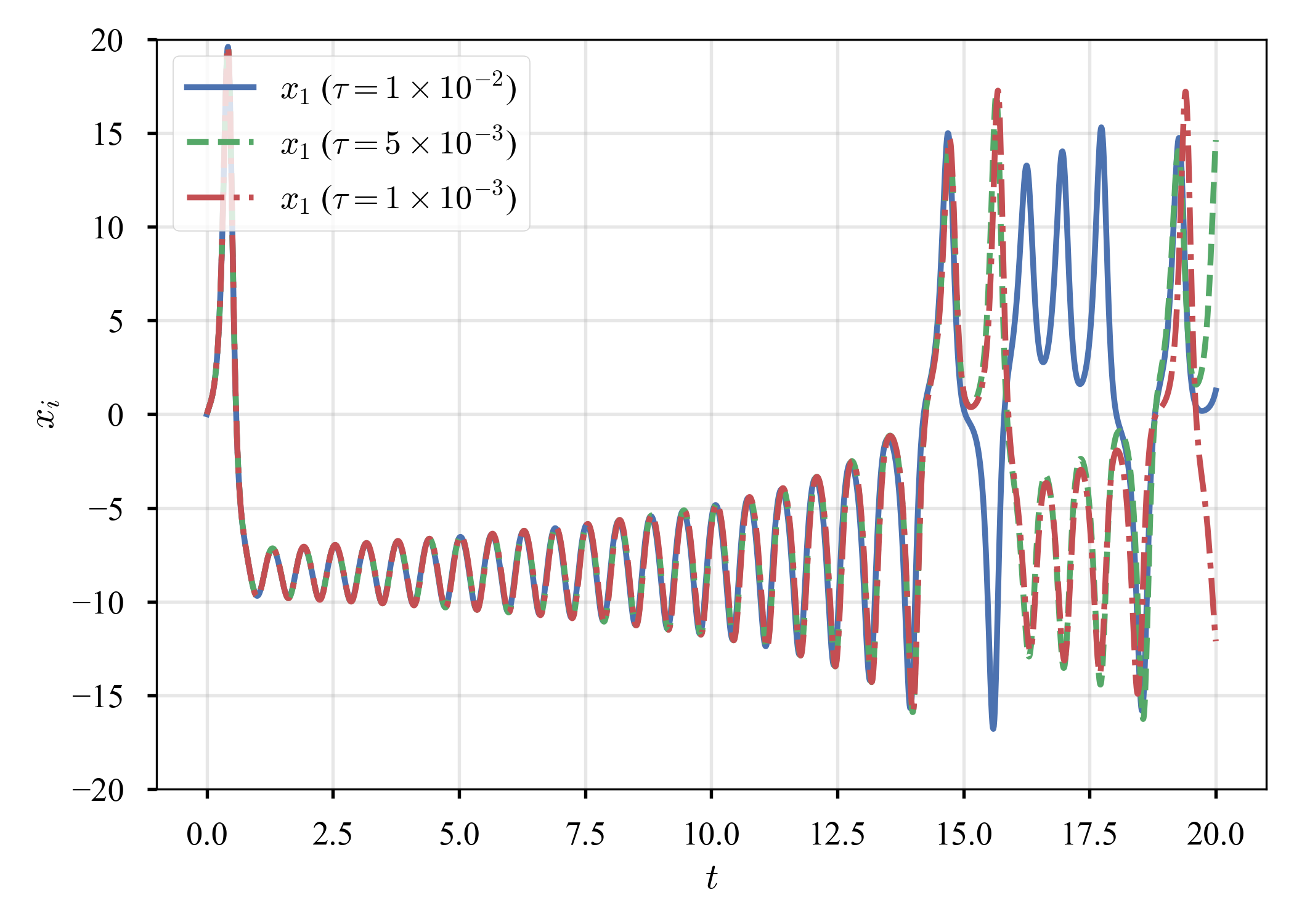
同じ時間積分法でも,時間増分が異なると(時間分解能の差),系の行き着く先は異なるのだろうか.$\left( x_1, x_2, x_3 \right) = (0, 1, 1.05)^{\top}$からスタート.見易さのため,$x_1$のみプロット.
| Euler | Heun | RK(4) |
|---|---|---|
 |
 |
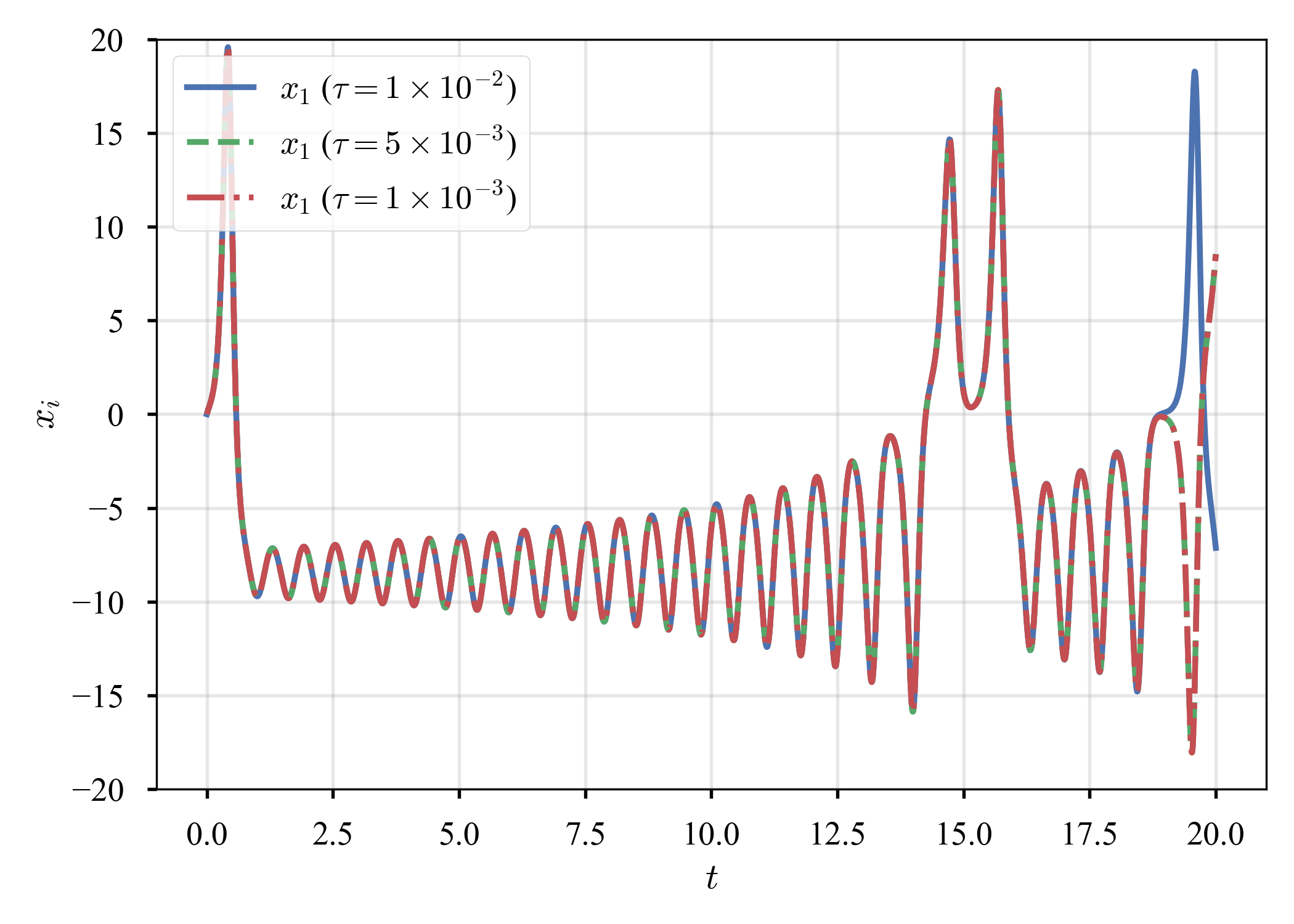 |
いずれの方法でも,長時間経つと異なる挙動を呈する.気になっていたら,若干の議論があった.結論が付いたようには見えないが,scipy.integrate.odeintやscipy.integrate.solve_ivpがデフォルトで使っているのは,この動画で説明されている幅制御のようだ?とだけメモしておく.
終わりに
若干,数値実験の纏まりが悪かったものの,幾つかの重要な事項を勉強できた.7年前,理解は全くであったものの,楽しみながら勉強していた頃を思い出す(今も勿論楽しいが,楽しさのベクトルが違ったように思う).
やり残したことが2つある.
-
本当は,定義を認める形ではなく,統一的にRK($s, p$)を導出したかった.適合条件は教科書から拾ってきたものなので,何故そうなるのか,味わい切れていない(そして間違っているかもしれないという恐怖がある).
-
SSP-RK(Strong Stability Preserving-Runge-Kutta method)だけは,名前の付け方からして,他のRKシリーズと違うのだろうか?これは未だ勉強できていない.SSP-RKシリーズは,1980~90年代に開発されてきたようである(例えば,Shu&Osher19887, Shu1988, Gottlieb&Shu1998, Gottlieb+2001, Gottlieb&Gottlieb2003),ということと,SSP-RK3を不連続Galerkin法に適用した例を見つけた(Kubatko+2014, Yeager+2021, 松本+2024)ということだけ,メモしておく.
区別すべきことが1つある.
Butcher2016の"22. Generalizations of the Euler Method"では,陽解法に関して,
- More computations in a step: multi-stage method
- Greater dependence on preveous values: multi-value method
- Use of higher derivatives: multi-derivative method
の分類を示している(同書p.95のFigure 224(i)が分かり易い).それぞれ,Runge-Kutta methods, Adams methods, Taylor series methodsと分類できる.ずっと私はRunge-Kutta族とAdams族の違いが良く分からなかったのだが,成程,これらの違いがすっきりした.
- Runge-Kutta methods -> single-step multi-stage methods
- Adams methods -> linear multi-step methods
- Adams-Bashforth method -> explicit
- Adams-Moulton methods -> implicit
しかし,考えてみると,Runge-Kutta族とAdams族には,英語ではstage, stepという違う言葉が割り当てられているのに,日本語ではどちらも段という.日本語訳はこういうところで混乱を生むので不便だ.そして残念なことに,stage, step両者に段という日本語を与える風習は浸透してしまっており,修復不可能である(修復しなければならないとは言わないが,私のように混乱する人間は少なからずいるのではないか,という傷の舐め合いのような言い訳だ...).
また,linear multi-step methodsの安定性に関して,それらがA-stableでないことが知られているらしい.Dahlquistの第1の障壁(Dahlquist1956)と第2の障壁(Dahlquist1963)がある.第1の障壁が達成可能な精度に関するもので,第2の障壁が如何なる陽的linear multi-step methodsもA-stableでないことを言っているようであるが,面白そうなのでしっかりと読んでみたい.宿題である.
Appendix
安定性解析
幾つかの教科書が,さらりと,「2段2次の方法の安定性領域はこれである」という話の展開をしている印象がある.しかし,例えば,Heun法と中点法はどちらも2段2次の方法だが,計算法が違うので,全く同じ安定性領域を持っているのか,俄かには信じ難いではないか?確認してみる.
2段2次
2段2次のHeun法:
\begin{align}
f_{1}
&= M u^{(n)} \\
f_{2}
&= M \left( u^{(n)} + \tau M u^{(n)} \right)
= \left( M + \tau M^2 \right) u^{(n)} \\
u^{(n+1)}
&= u^{(n)} + \tau \frac{1}{2}
\left(
M u^{(n)} + \left( M + \tau M^2 \right) u^{(n)}
\right) \\
&= \left( I + \tau M + \frac{\left( \tau M \right)^2}{2} \right) u^{(n)} \\
\end{align}
2段2次の一般形:
\begin{align}
f_{1}
&= M u^{(n)} \\
f_{2}
&= M \left( u^{(n)} + \theta \tau M u^{(n)} \right)
= \left( M + \theta \tau M^2 \right) u^{(n)} \\
u^{(n+1)}
&= u^{(n)} + \tau
\left(
\left( 1 - \frac{1}{2 \theta} \right) M u^{(n)}
+ \frac{1}{2 \theta} \left( M + \theta \tau M^2 \right) u^{(n)}
\right) \\
&= \left( I + \tau M + \frac{\left( \tau M \right)^2}{2} \right) u^{(n)} \\
\end{align}
より,Heun法,中点法,Ralston法が同じ安定性領域を持っていることが分かる.
3段3次
3段3次のHeun法:
\begin{align}
f_{1} &= M u^{(n)} \\
f_{2}
&= M \left( u^{(n)} + \tau \frac{M}{3} u^{(n)} \right)
= \left( M + \tau \frac{M^2}{3} \right) u^{(n)} \\
f_{3}
&= M \left( u^{(n)} + \tau \frac{2}{3} \left( M + \tau \frac{M^2}{3} \right) u^{(n)} \right)
= \left( M + \frac{2}{3} \tau M^2 + \frac{2}{9} \tau^2 M^3 \right) u^{(n)}
\\
u^{(n+1)}
&= u^{(n)} + \tau \left( \frac{1}{4} M u^{(n)} + \frac{3}{4} \left( M + \frac{2}{3} \tau M^2 + \frac{2}{9} \tau^2 M^3 \right) u^{(n)} \right) \\
&= \left( I + \tau M + \frac{\left( \tau M \right)^2}{2} + \frac{\left( \tau M \right)^3}{6} \right) u^{(n)} \\
\end{align}
Butcher tableauより:
\begin{align}
f_{1}
&= M u^{(n)} \\
f_{2}
&= M \left( u^{(n)} + \tau a_{21} M u^{(n)} \right) \\
&= \left( M + \tau a_{21} M^2 \right) u^{(n)} \\
f_{3}
&= M \left(
u^{(n)} + \tau \left(
a_{31} M u^{(n)} + a_{32} \left( M + \tau a_{21} M^2 \right) u^{(n)}
\right)
\right) \\
&= M \left(
I + \tau \left(
a_{31} M + a_{32} \left( M + \tau a_{21} M^2 \right)
\right)
\right) u^{(n)} \\
&= \left(
M + \tau \left(
a_{31} + a_{32} \right) M^2 + \tau^2 a_{32} a_{21} M^3
\right) u^{(n)} \\
u^{(n+1)}
&= u^{(n)}
+ \tau \left(
b_{1} f_{1}
+ b_{2} f_{2}
+ b_{3} f_{3}
\right) \\
&= u^{(n)}
+ \tau \left(
\left( b_{1} + b_{2} \right) M u^{(n)}
+ \tau \left(
a_{21} b_{2}
+ \left( a_{31} + a_{32} \right) b_{3}
\right) M^2 u^{(n)}
+ \tau^2 \left(
a_{32} a_{21} b_{3}
\right) M^3 u^{(n)}
\right) \\
&= \left(
I
+ \tau \left(
\left( b_{1} + b_{2} \right) M
+ \tau \left(
a_{21} b_{2}
+ \left( a_{31} + a_{32} \right) b_{3}
\right) M^2
+ \tau^2 \left(
a_{32} a_{21} b_{3}
\right) M^3
\right)
\right) u^{(n)} \\
\end{align}
本文で列挙した手法はいずれも,
\begin{align}
b_{1} + b_{2}
&= 1 \\
a_{21} b_{2} + \left( a_{31} + a_{32} \right) b_{3}
&= \frac{1}{2} \\
a_{32} a_{21} b_{3}
&= \frac{1}{6}
\end{align}
を満たす(というか,こちらが適合条件か?分からなくなってきた...).すなわち,3段3次の方法はいずれもが同一の安定性領域を持っている.
-
"Butcher tableau"の名前から,RungeやKuttaなどと同時期の先生かと思っていたが,ご存命だ.NZにいらっしゃるらしい. ↩
-
周辺の教科書,文献を幾つか読んだところ,$dy / dx = f \left( x, y (x) \right)$と書くことが一般的なようだ.しかし個人的な感覚として,$x, y$は空間の広がりをイメージしてしまうので,解を$u$と書くことにし,時間発展を意識して独立変数を$t$と書くことにした.これに伴い,刻み幅を$\tau$と書くことにした(刻み幅を$h$と書くのが慣例のようだが,これもやはり空間方向への離散化パラメータをイメージしてしまう). ↩
-
RK(4)とか古典的Runge-Kutta法などと呼ぶ場合もある(寧ろ,その方が多い気がする). ↩
-
Heun法のことを改良Euler法(improved Euler method),中点法のことを修正Euler法(modified Euler method)と呼ぶ場合もあるようだが,混乱が多いので,この名前の付け方は個人的に好まない.色々と調べ,色々な人の文章を読んだが,皆が混乱しているようだ.だから,ここに書いた "Heun法が改良Euler法で,中点法が修正Euler法" というのも,本当は彼辺此辺かもしれない. ↩
-
ああ,なんと懐かしいのだろう!学士課程2年目に受講したODEの講義に登場したことを今でも覚えている.当時,ODEを担当してくださった先生にKhan Academyを紹介してもらい,良く見ていた. ↩
-
学士課程3年次の留学中に学んだ.交通工学の授業だったが,その中のProjectと呼ばれる自由課題で,Gompertz curveを用いて交通流の増加をモデリングしたことを記憶している. ↩
-
因みに,OsherはLSM(Level-Set Method, Dervieux&Thomasset1980, Osher&Sethian1988)を作り上げてきた人の一人. ↩