硬い微分方程式を解く

この記事では硬い線形項が存在する非線形な常微分方程式を数値的に解く方法を解説し、Rustのライブラリであるeomを使用して乱流の自己再帰的なカスケードのモデルであるGOYシェルモデルを数値的に解いてみます。

硬い微分方程式とは

数学において硬い方程式（英: stiff equation）は、近似解を計算するためのある数値的方法が、刻み幅を極めて小さくしない限り、数値的不安定になる微分方程式である。
硬い方程式 - Wikipedia

特に時間一階の微分の初期値問題
$$
\frac{dx}{dt} = f(x(t), t), x(0) = x_0
$$

において「硬い」とは時間方向に1step進める際の増分を十分小さくとるために差分$\Delta t$を非常に小さくとる必要がある問題の事です。簡単のためにオイラー法で考えてみましょう：
$$
x(t+ \Delta t) = x(t) + \Delta t f(x(t), t)
$$
方程式が硬くなる例として$f(x) = -10^5x$の場合を考えてみましょう。これはちょうど物体が非常に強い摩擦力が働いている場合の運動方程式ですね（$x$が速度)。強い摩擦で瞬く間に物体は静止してしまうはずです。この場合にどのように$\Delta t$を決めれば良いでしょうか？

$\Delta t = 10^{-3}$程度では右辺第2項の絶対値は$10^2 x$となり全然小さくない量になってしまいます。最初に$x=+1$の速度で右に移動していた物体が次のステップで摩擦力によって逆の方向$x=-99$に加速されたことになってしまいます！
これを回避するためには$\Delta t$をもっと小さく$\Delta = 10^{-8}$くらいにしないといけません。しかしそれではシミュレーションは全く進みません。これは困りました(´・ω・｀)

でもちょっと待ってください、我々は線形の微分方程式なら解析的に解くことができたはずです。一般に$f(x) = Ax$とすると、初期値問題の解は
$$ x(t) = e^{At} x(0) $$
で与えられます。これを使えば
$$ x(t+\Delta t) = e^{A \Delta t} x(t) $$
ですが、実際に$A \Delta t = -10^2$を入れてみると$\exp(A \Delta t) = 3.7 \times 10^{-44}$となり、それはもう一瞬で止まることが分かります。

※ここでは$\exp(At)$を上手く扱うために$A$が対角行列の場合を考えます。これは一般に$A$が対角化可能であれば座標変換で達成できるのでそこまで強い仮定ではありません。

非線形な場合

線形の場合には解析解を利用することで上手くいことが分かりました。では非線形な場合にはどうでしょう？もちろん現実的な問題では線形な微分方程式ばかりではないので線形な場合にしか使えない手法ではどうしようもありません。しかし一般の非線形な場合を考える前に次のような場合を考えましょう：
$$
\frac{dx}{dt} = g(x) + Ax
$$
$g(x)$が「硬くない」非線形項、$Ax$が硬い線形項の場合です。一番「硬い項」が線形で入ることはよくあり、例えば流体系において粘性に由来する硬い方程式系は基本的にこの形になります（$g(x)$が移流に対応する)。界面がある場合や、化学反応に由来する場合は非線形項の側が硬くなることもあります。今回はこの場合は扱いません　( TДT)ｺﾞﾒﾝﾖｰ

さて上で見た通り、線形項$Ax$が硬いという事はその絶対値が硬くない$g(x)$より非常に大きいという事です。つまりこの方程式の右辺はほとんど$Ax$という事になります。という事はこの方程式の解は$x(t) = e^{At} x(0)$に近くなると予想されますが、追加項の分だけずれるはずなので、それを含めて新しい変数$y(t)$を導入しましょう：
$$x(t) = e^{At}y(t)$$
$t=0$で$x(0) = y(0)$を満たすように作っています。積の微分公式より、
$$
\frac{dx}{dt} = e^{At}\frac{dy}{dt} + Ae^{At}y(t) = e^{At}\frac{dy}{dt} + Ax
$$
元の式と合わせて
$$
e^{At}\frac{dy}{dt} = g(e^{At}y)
$$
となります。これが線形部分の効果だけによる解$e^{At}$からの”ずれ”の方程式です。この右辺の項は硬くないので、この形で離散化してみましょう：
$$
e^{A(t+\Delta t)}\frac{y(t+\Delta t) - y(t)}{\Delta t} = g(e^{At}y(t))
$$
元の変数に戻すと、
$$
x(t+\Delta t) = e^{A \Delta t} [x(t) + \Delta t g(x(t)) ]
$$
これが硬い方程式用のオイラー法の離散化となります。

GOY shell model

さて理論はこのくらいにして数値計算をしてみましょう。

硬い常微分方程式の例として乱流のカスケードのモデルであるGOYシェルモデルを考えましょう：
$$
\left(\frac{d}{dt} + \nu k_n^2\right) u_n = g(u) + f\delta_{n, 4}
$$
$n = 0,...,26$, $u_n$は複素数($u_n^*$が複素共役)。$k_n = k_0 2^n$, $k_0 = 0.0625$。27次元の複素数の常微分方程式です（非線形項$g(x)$はややこしいから略、論文かeomの実装を読んでね）。左辺に移項してある$\nu k_n^2$が線形項$A$で、$k_{26}^2 = k_0^2 2^{52}$なことから非常に硬い方程式になります。

乱流は様々な大きさの渦が共存し、それらが非線形に相互作用を繰り返す系として知られていますが、各スケール($k_n$)の速度場の”大きさ”($u_n$)をモデル化したものがこの方程式になります（実際にはNavier-Stokes方程式をFourier変換して、移流と圧力の効果を近似すると得られる）。このように計算するべき時間スケールに対して短いスケールの運動が系に含まれるとき、一般に運動方程式は硬くなります。

eom crate

ここでは私の運動方程式(Equation of Motion, EOM)のソルバーを使います：

https://github.com/termoshtt/eom
Configurable ODE/PDE solver

eomではこのように対角化してある行列の対角成分を与える関数diagと非線形項$g(x)$を与える関数nlinをSemiImplicit trait経由で実装することで時間発展のコードを生成することができます。"semi-implicit"というのは方程式の一部を陰的に(implicit)解くための手法の総称です。今回の例では非線形項$g(x)$を陽的に、粘性項を陰的に（実際は解析的に）解いていることに対応します。

impl SemiImplicit for GoyShell {
    fn nlin<'a, S>(&mut self, v: &'a mut ArrayBase<S, Ix1>) -> &'a mut ArrayBase<S, Ix1>
    where
        S: DataMut<Elem = c64>,
    {
        let mut am2 = c64::zero();
        let mut am1 = c64::zero();
        let mut a_0 = v[0].conj();
        let mut ap1 = v[1].conj();
        let mut ap2 = v[2].conj();

        let a = 1.0;
        let b = -self.e;
        let c = -(1.0 - self.e);

        for i in 0..self.size {
            v[i] = self.k(i) * (a * ap1 * ap2 + 0.5 * b * ap1 * am1 + 0.25 * c * am1 * am2);
            am2 = am1;
            am1 = a_0;
            a_0 = ap1;
            ap1 = ap2;
            if i + 3 < self.size {
                ap2 = v[i + 3].conj();
            } else {
                ap2 = c64::zero();
            }
        }

        v[self.f_idx] = v[self.f_idx] + c64::new(self.f, 0.0);
        v
    }

    fn diag(&self) -> Array<c64, Ix1> {
        (0..self.size)
            .map(|n| self.nu * self.k(n) * self.k(n))
            .collect()
    }
}

このGoyShellはサンプルとしてsrc/ode/goy_shell.rsに実装されています。これは以下のように使えます：

let dt = 1e-5;
let eom = ode::GoyShell::default();
let mut teo = semi_implicit::DiagRK4::new(eom, dt);

DiagRK4構造体は上の硬い方程式用のオイラー法の代わりに古典的Runge-Kuttaに置き換えたものです。これはSemiImplicitを実装している任意の構造体を受け取れます。DiagRK4はTimeSeries traitを実装してるのでシミュレーションの時系列をIteratorとして得ることができる:

let ts = eom::adaptor::time_series(x0, &mut teo);

iteratorに出来たので、これは前回のasinkを用いてストレージに流し込める

for (t, v) in ts.take(setting.duration).enumerate() {
    if t % setting.skip == 0 {
        let doc = Doc {
            time: t as f64 * setting.dt,
            data: v.to_vec(),
        };
        sender.send(doc).expect("Failed to send doc");
    }
}

$u_4, u_8, u_{16}, u_{26}$の実部の時系列をプロットしたものが下図になります。

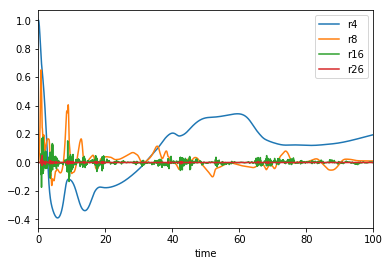
このようにゆっくりしたダイナミクス$u_4$と非常に早いダイナミクス$u_{16}, u_{26}$が共存したシステムになります。

最後に

硬い方程式の簡単な解説から、eomによる実装まで駆け足な記事になってしまいました。マルチスケールなダイナミクスのシミュレーションの参考になれば幸いです。