導入
「Flipによるドロネー三角形分割」を利用したボロノイ図描画のアルゴリズムを一部改良してJavaで実装しました。まずは前置きをしておきましょう。
ボロノイ図とは？
Wikipediaより引用
ボロノイ図（Voronoi diagram）は、ある距離空間上の任意の位置に配置された複数個の点（母点）に対して、同一距離空間上の他の点がどの母点に近いかによって領域分けされた図のことである。特に二次元ユークリッド平面の場合、領域の境界線は、各々の母点の二等分線の一部になる。
つまり、ある点に最も近い母点を探したいときに大変便利な図表と言えます。この図（＝境界線をなす線分の集合）を計算することを目標にします。
ボロノイ図とドロネー図
ボロノイ図と関係の深い図としてドロネー図（Delaunay diagram）と呼ばれるものがあります。ドロネー図（もしくはドロネー三角分割）とは空間上の母点の集合（緑の点）に対しある規則に従い点と点を結んで空間を三角形分割したものです（赤線）。そして分割された三角形の外接円の中心（黄色の点）を結ぶボロノイ図（青線）が現れます。詳細は[Qiita]ボロノイ図を作るが参考になります。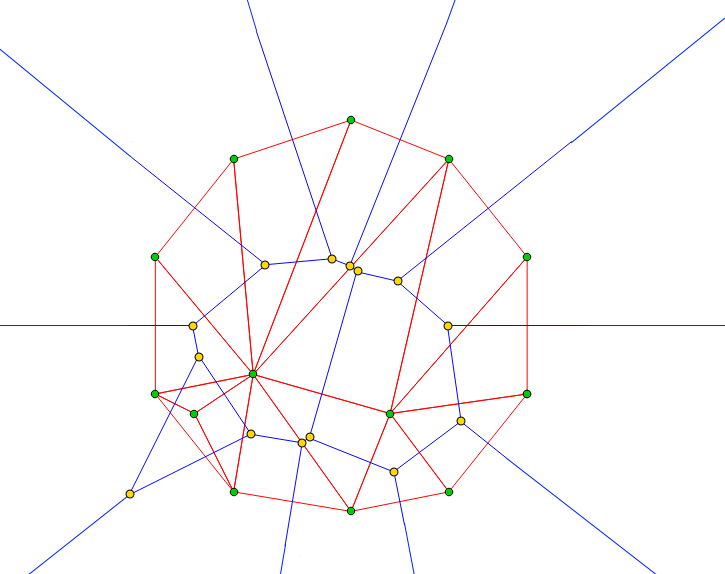
図は[Qiita]ボロノイ図を作るから引用、一部改変
アルゴリズム
ドロネー図からボロノイ図が簡単に計算できることが分かったのでドロネー図の計算方法が分かれば十分です。アルゴリズムを紹介する文献は沢山あるのでここでは詳細を省略します。
今回は実装が簡単という理由で「Flipによるドロネー三角形分割」を採用します。アルゴリズムの流れは以下の通りです。
\begin{align}
&P_A \equiv \{母点P \in \mathbb{R}^2の集合\} \\
&\triangle{T_A} \leftarrow (\forall P \in P_A を内部に含む三角形) \\
&Q \leftarrow P_A \quad 待ち行列 \\
&T \leftarrow \{\triangle{T_A}\} \quad 分割された三角形の集合\\
&\mathrm{while} \;(\;Q \ne \varnothing\;)\\
&\quad Q \;\verb|>|\verb|>|\; P \in P_A \quad 母点Pをポップ \\
&\quad \exists \triangle{ABC} \in T \; st. \; 母点Pは三角形ABCの内部に含まれる \\
&\quad T \leftarrow T \,\verb|\|\{\triangle{ABC}\} \quad 三角形ABCを取り除く\\
&\quad T \leftarrow T\cup \{\triangle{ABP},\triangle{BCP},\triangle{CAP}\} 三角形ABCを点Pで分割して追加\\
&\quad S \leftarrow \{AB,BC,CA\} \quad 各辺をスタックに積む\\
&\quad \mathrm{while}\;(\;S\ne \varnothing\;) \\
&\quad\quad S \;\verb|>|\verb|>|\; AB \quad 辺ABをポップする\\
&\quad\quad \exists\triangle{ABC},\triangle{ABD} \in T \quad 辺ABを持つ三角形を探す\\
&\quad\quad \mathrm{if}\;(\;\triangle{ABC}の外接円に点Dが含まれる\;)\\
&\quad\quad\quad 辺ABを\mathrm{Flip}する\\
&\quad\quad\quad S \;\verb|<|\verb|<|\;AC,AD,BC,BD \quad スタックに辺を追加\\
&T \leftarrow \{\triangle{t} \in T \;\verb|||\;\triangle{t}は\triangle{T_A} と頂点を共有しない\}
\end{align}
こうして得られたドロネー三角分割の隣り合う２つ三角形の外心を結んでいけば目的のボロノイ図が得られます。ただし、一番外側に位置する三角形に関しては外心から隣り合う三角形がない方向へ直線を引いてやる必要があります（上の図で画面外側へはみ出ている直線に相当）。そうすれば平面全体が分割されます。
困った…
先人の知恵を借りてさぁ実装！してみたのですが少々困った問題に遭遇しました。
使用したデータ
日本の鉄道駅のデータを駅データ.jpから利用。9000くらい存在する駅の位置座標を使います。
注意 以降の実験では簡単のため経度・緯度をユークリッド平面のXY座標に読み替えています。よく目にするメルカトル図法の地図上で直線を引く感じなので、実際の球面上の直線（測地線）とは一致しません。また経度・緯度でユークリッド距離を計算するというヤバイ実装なので高緯度では東西方向の距離が実際の値より誇張されるのに留意してください。
三角形の辺上に点が追加されると失敗する
前述の「Flipによるドロネー三角形分割」では母点を逐次的に追加していくのですが、そのとき追加する点を内包する三角形を探す処理があります。しかし今回用いた駅のデータセットだと追加順序によっては三角形の辺上に追加される場合がありました。すると一直線上の３点から三角形を定義しようとして以降の処理が破綻します。
外周部のボロノイ図が何かおかしい
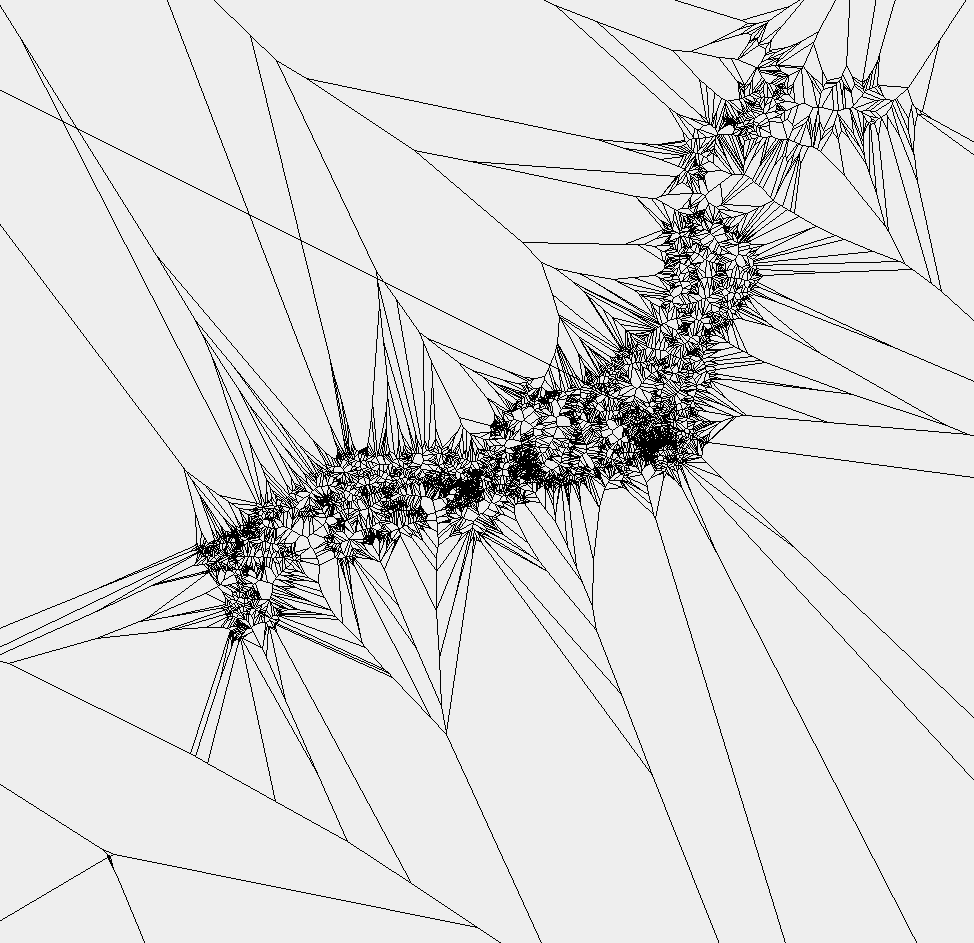
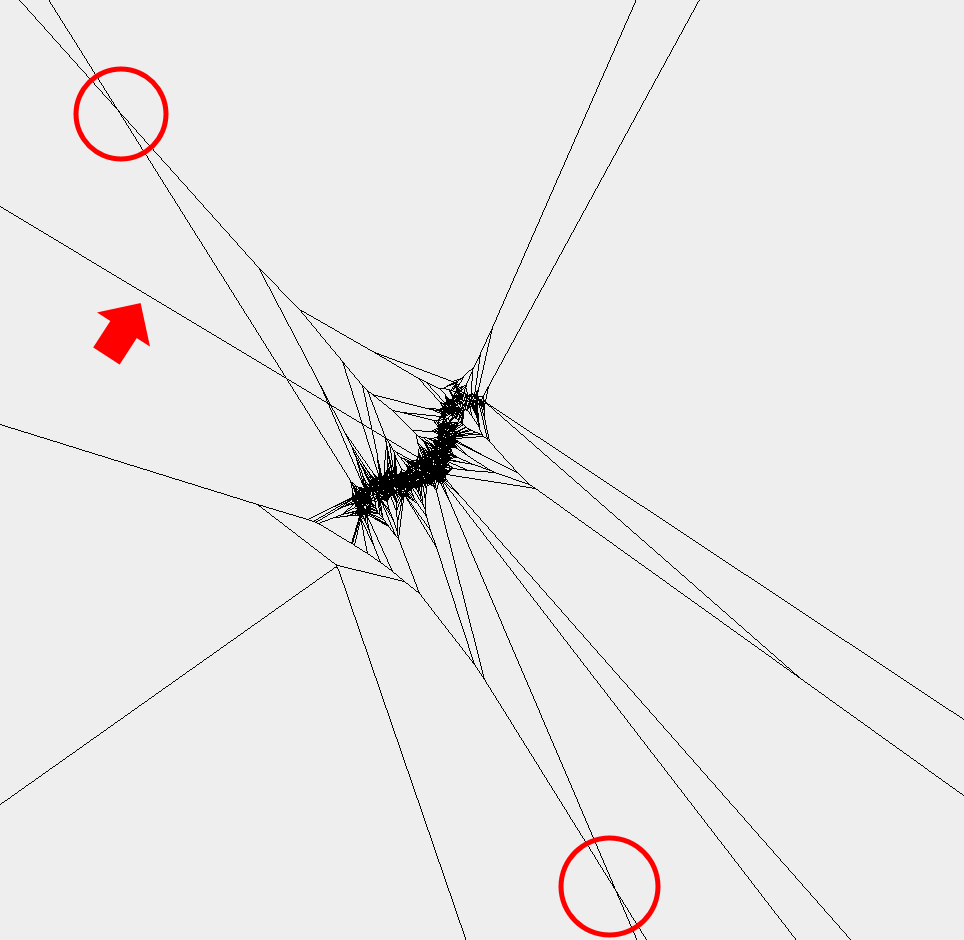
「ある点に最も近い母点を探したい」という問題解決を想定しているので、平面全体をボロノイ図で分割したいという欲求がありました。そこでドロネー図から変換する際に「一番外側に位置する三角形に関しては外心から隣り合う三角形がない方向へ直線を引く」処理を付加したのですが、ここで問題発生。下に駅のデータで実際にボロノイ図を計算して描画したものを示します。
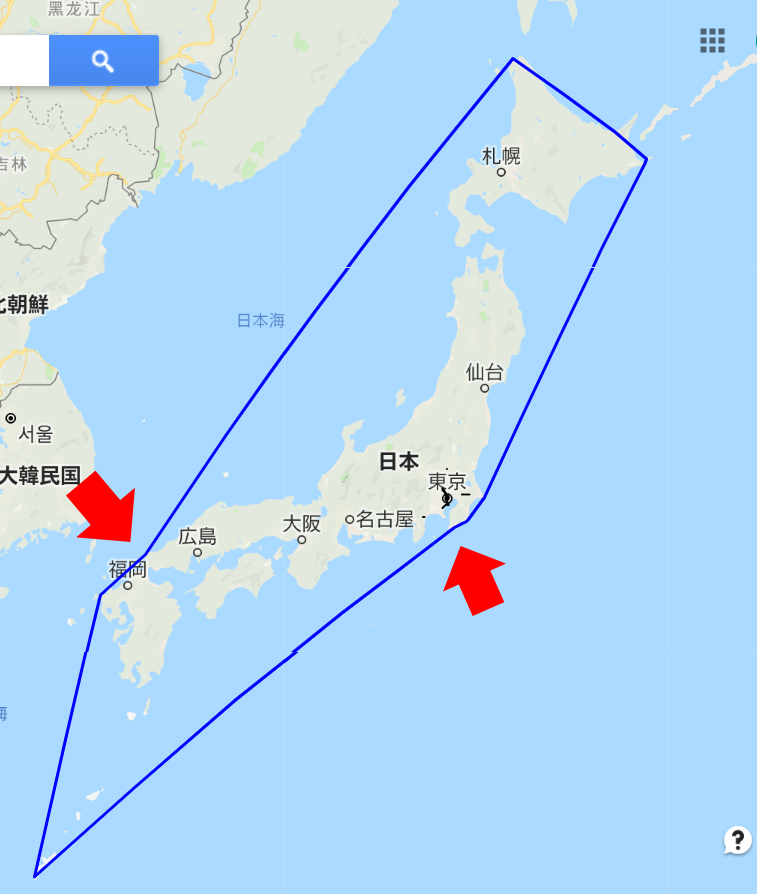上の図は「Flipによるドロネー三角形分割」の最後の過程で「一番外側に設定した適当な入れ物の三角形と頂点を共有する三角形を除去」した後に外郭を成すポリラインを描画したものです。何か凹の部分があような…？！先ほどの変な交点 ＞ そこに外心をもつ三角形が実は別に存在する ＞ その三角形とは外郭の凹んでいる部分？とビック仮定をおいて改良を試みます。
解決すべき問題
- そんな三角形tは存在しないから母点を追加できない
対象処理： $\exists \triangle{t} \in T ; st. ; 母点Pは三角形tの内部に含まれる$ - ドロネー図の外郭の多角形が凸でない
対象処理：あらたな処理の追加が必要
改良
まずは三角形の辺上に母点が追加される場合の対応から。
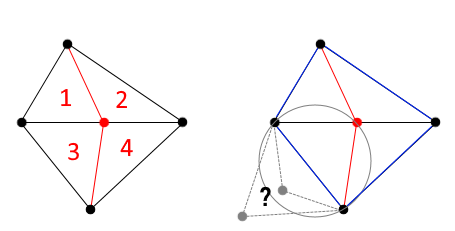
アルゴリズムの原則として母点（赤い点）をどんどん追加しながら三角形分割するので、とりあえず左の図のように４つの三角形に分割します。この新たな分割により生じた外接円特性を満たさない可能性のある隣接する三角形の組が右図のように４つ考えられます。ですから三角形の組が共有する辺（青い線分）をスタックに積み同様のFlip操作を行っていきます。
次に外郭が凸でない問題に対処します。
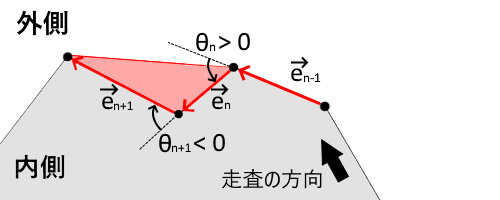
まずは従来通り処理して外郭を頂点のリストとして取得します。そしてリストを走査しながら凹の部分を発見次第あらたな三角形で埋めて全体を凸にします（図参照）。以降角度の正方向と走査の方向を左回りとします。隣接する辺について走査方向のベクトル$\vec{e_n}$と$\vec{e_{n+1}}$のなす角が外角$\theta_{n+1} = \tan^{-1}\left(\frac{\vec{e_n} \times \vec{e_{n+1}}}{\vec{e_n}\cdot ;\vec{e_{n+1}}}\right)$になります（ただし$-\pi/2 < \theta_{n+1} < \pi/2$を仮定）。この値が負なら凹んでいるのが分かります。実装では追加された三角形で外接円特性が満たされなくなる場合も考慮しました（そんな場合があるのかは不明）。
改良後のアルゴリズム
以上の改良を踏まえたドロネー図のアルゴリズムを整理
\begin{align}
&P_A \equiv \{母点P \in \mathbb{R}^2の集合\} \\
&\exists \triangle{T_A} \;st.\; \forall P \in P_A \;\mathrm{inside}\; \triangle{T_A} \\
&Q \leftarrow P_A \\
&T \leftarrow \{\triangle{T_A}\}\\
&\mathrm{while} \;(\;Q \ne \varnothing\;)\\
&\quad Q \;\verb|>|\verb|>|\; P \in P_A \\
&\quad \mathrm{if} \;(\;\exists \triangle{ABC} \in T \; st. P \;\mathrm{inside}\; \triangle{ABC}\;) \\
&\quad\quad T \leftarrow T \,\verb|\|\{\triangle{ABC}\} \\
&\quad\quad T \leftarrow T\cup \{\triangle{ABP},\triangle{BCP},\triangle{CAP}\} \\
&\quad\quad S \leftarrow \{AB,BC,CA\} \\
&\quad \mathrm{else\; if}\;(\exists \triangle{ABC},\triangle{ABD} \in T \; st. P \;\mathrm{on}\; AB\;)\\
&\quad\quad T \leftarrow T \,\verb|\|\{\triangle{ABC},\triangle{ABD}\} \\
&\quad\quad T \leftarrow T\cup \{\triangle{PAC},\triangle{PAD},\triangle{PBC},\triangle{PBD}\} \\
&\quad\quad S \leftarrow \{AC,AD,BC,BD\} \\
&\quad \mathrm{while}\;(\;S\ne \varnothing\;) \\
&\quad\quad S \;\verb|>|\verb|>|\; AB\\
&\quad\quad \exists\triangle{ABC},\triangle{ABD} \in T \\
&\quad\quad \mathrm{if}\;(\;\triangle{ABC}の外接円に点Dが含まれる\;)\\
&\quad\quad\quad 辺ABを\mathrm{Flip}する\\
&\quad\quad\quad S \;\verb|<|\verb|<|\;AC,AD,BC,BD \\
&T \leftarrow \{\triangle{t} \in T \;\verb|||\;\triangle{t}は\triangle{T_A} と頂点を共有しない\}\\
&T \leftarrow T \;\cup\; \{Tの外郭が凹んでいる部分の三角形\}
\end{align}
実装
今回はJavaで実装し実験しました。アルゴリズムをプログラムに落とし込む際の技術的な話は一切していませんが、ソースコードはこちらで公開しているので適宜参照してください。
結果
うまくいった。まずドロネー三角分割から
問題だった一番外側を囲む多角形が凸になっています。高緯度とは言え北海道スカスカですわ。次は肝心のボロノイ図です
