GoogleMap の座標系を理解する

疑問

GoogleMapsAPIを利用するとき、

• GoogleMap で表示される1ピクセルは何メートル？
• 目的の領域を GoogleMap で表示するのに最適な zoom_levelは？

などなど。

現在使用されている主要な測地系では地球を回転楕円体として扱いますが、ここでは簡単のため、地球は半径 $\rm{R}=6.3781 \times 10^6 ~\rm{m}$ の完全な球体と仮定して話ます。
[日本測地学会] 地球の形をどのように記載するか
[Wikipedia] 地球半径

メルカトル図法

丸い地球を平らな地図上で表現するためには、地球上の各位置（緯度,経度）を地図上のxy座標に変換する必要があります。これが投影法であり、GoogleMapsAPI など多くの地図ではメルカトル図法が用いられています。まず、座標の変数を次のように定めます（角度はラジアン）。

\begin{array}
\mbox{地球上の座標} \ &\left\{
\begin{array}{l}
\mbox{緯度}\ \phi &(-\cfrac{\pi}{2} \le \phi \le \cfrac{\pi}{2})\\
\mbox{経度}\ \lambda &(-\pi \le \lambda \le \pi)\\
\end{array}
\right. \\
\mbox{平面上の座標} \ &\left\{
\begin{array}{l}
\mbox{緯線方向}\ x &(-{\rm R} \pi \le x \le {\rm R} \pi)\\
\mbox{経線方向}\ y &(-{\rm R} \pi \le y \le {\rm R} \pi)\\
\end{array}
\right. \\
\end{array}

赤道上の長さが保存されるように投影する変換式は

\left\{
\begin{array}{l}
x = {\rm R}\ \phi \\
y = {\rm R}\ \ln \left({\rm tan}\left(\cfrac{\pi}{4} + \cfrac{\phi}{2} \right)\right) 
\end{array}
\right.

経線はy軸平行な直線に、緯線はx軸平行な直線にそれぞれ写されます。

図は [Wikipedia] 投影法 (地図)、地図投影法学習のための地図画像素材集 より引用、一部改変

変換式によれば $y$ の範囲は $-\infty \le y \le +\infty$ となりますが、面積が有限の地図で無限は表現できないため、地図全体が正方形になるように $-{\rm R} \pi \le y \le {\rm R} \pi$ の範囲で切り取るのが通例です。緯度に換算すると大体±85度になり、極は表示されません。とりあえず微分して、

\begin{array}{l}
\cfrac{\mathrm{d} \lambda}{\mathrm{d} x} = \cfrac{1}{\rm R} \\
\cfrac{\mathrm{d} \phi}{\mathrm{d} y} = \cfrac{1}{\rm R}\ {\cos\phi}
\end{array}

緯線上では、$x$ と経度 $\lambda$ の比率は一定で各経線は等間隔で並びます。一方で経線上では、$y$ と緯度$\phi$ の比率は $\cos\phi$ に依存し、各緯線の間隔は高緯度ほど広がります。

メルカトル図法については別記事で詳説しています

GoogleMap の座標系

GoogleMaps API でも緯度・経度との変換にメルカトル図法の投影を用いています。詳細は公式ドキュメントを読むのが早いです。

Tile（タイル）

GoogleMaps ではタイルと呼ばれる256x256サイズの画像をつなぎ合わせて地図を表現しています。ズームレベル $z$（縮尺）や場所に応じて適当なタイルを取得してきて貼り合わせるイメージです。

World coordinates（ワールド座標）

全世界（緯度＜85度）を1枚のタイルで表現したとき、画像中のピクセルの位置で指定したのがワールド座標です。また、このときをズームレベル $z=0$ と定義します。

ワールド座標 $(x_{\rm w}, y_{\rm w})$ は整数に限らず実数値をとり、その範囲は

0 \le x_{\rm w}, y_{\rm w} \le 256

先ほどの $(x,y)$ からの変換式は、

\left\{
\begin{array}{l}
x_{\rm w} = 128 \left( \cfrac{x}{{\rm R}\pi} + 1 \right) \\
y_{\rm w} = 128 \left( 1 - \cfrac{y}{{\rm R}\pi}\right) 
\end{array}
\right.

Pixel coordinates（ピクセル座標）

ズームレベル $z$ が1増えるごとに2倍拡大されて、世界を表すタイルが縦横 $2^z$ 枚ずつの計 $ 2^{2z}$ 枚になります。タイル全体のサイズは $256\times2^z$ px に増えます。図は $z=2$ のときの様子です。

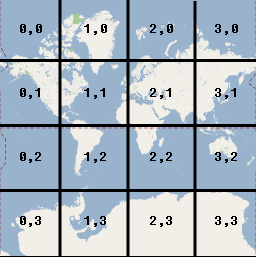
このとき、タイル全体中のピクセルの位置で指定したのがピクセル座標 $(x_{\rm p},y_{\rm p})$ であり、ワールド座標から次のように変換されます。

\left(\begin{array}{c}
 x_{\rm p} \\ y_{\rm p}
\end{array}\right) = 2^z
\left(\begin{array}{c}
 x_{\rm w} \\ y_{\rm w}
\end{array}\right)
\in \left[\,0, 256\times 2^z\,\right]^2

ズームレベル $z$ は整数に限らず0以上の実数に拡張され、$z=0$ のときはワールド座標と一致します。このピクセル座標こそが Google Map 上の任意の点と緯度・経度を1対1に対応させる要になります。

ピクセル座標における長さはWeb表示上の仮想ピクセルに相当します

ディスプレイの画素密度によっては物理ピクセル（キャプチャしたスクリーンショットのピクセル単位）とは異なる場合があります。

Maps JavaScript API での例

zoom_level = 0

ピクセル座標とワールド座標が一致するため全世界は$(x_{\rm p}, y_{\rm p}) = (x_{\rm w}, y_{\rm w}) \in [0,256]^2$の範囲に収まります。
図のように 256x256 px の大きさに全世界がちょうど表示されています。

zoom_level = 1

2倍拡大されて計4枚のタイルで全世界が表現されます。ピクセル座標の範囲は $(x_{\rm p}, y_{\rm p}) \in [0,512]^2$ となります。図のように赤道1周は 512 px になります。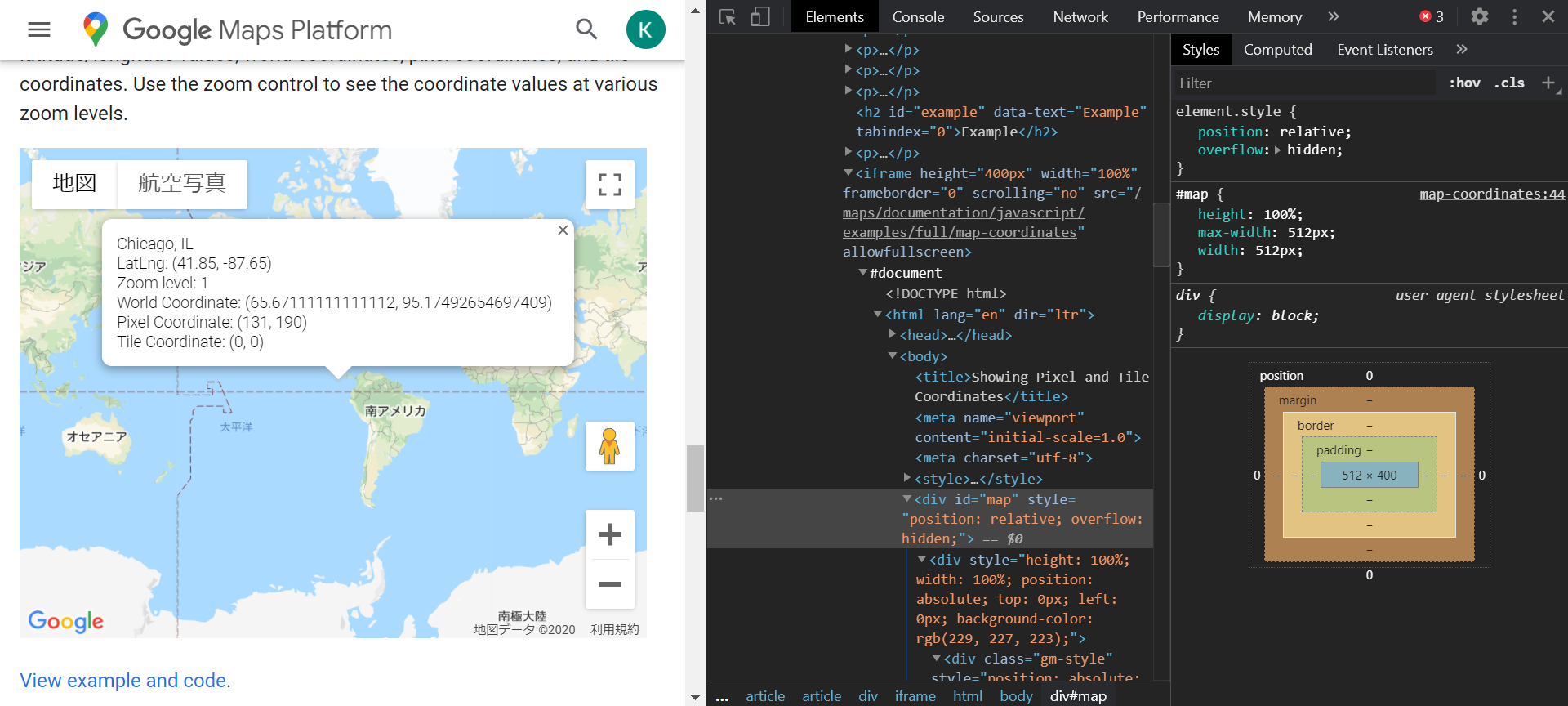

活用

これら知識を用いて最初の疑問に答えてみます。

1ピクセルは何メートル？

緯線

メルカトル図法では緯線が水平な直線になります。図のような経線上の1ピクセルの距離は？

• ズームレベル $z=14.75$
• 緯度 $\phi = 35.67483 \ [{\rm deg}]$

まずはピクセル座標 $x_{\rm p}$ と経度 $\lambda$ の関係を調べると、

\cfrac{\mathrm{d} \lambda}{\mathrm{d} x_{\rm p}} = \cfrac{\mathrm{d} \lambda}{dx}\cfrac{\mathrm{d} x}{\mathrm{d} x_{\rm w}}\cfrac{\mathrm{d} x_{\rm w}}{\mathrm{d} x_{\rm p}} = \cfrac{1}{\rm R}\ \cfrac{{\rm R}\pi}{128} \ 2^{-z} = \cfrac{\pi}{128 \times 2^z}

緯度 $\phi$ の緯線上の長さ $l_{\lambda}$ の変化量は $\Delta l_{\lambda} = {\rm R}\ \cos\phi \ \Delta \lambda$ だから、

\cfrac{\mathrm{d} l_{\lambda}}{\mathrm{d} x_{\rm p}} = \cfrac{\pi{\rm R}}{128 \times 2^z} \ \cos\phi

具体的な値を計算すると $\Delta l_{\lambda} = 493.81047\ldots~$ となり大体 500 m に一致します

経線

同様にして、経線上の長さ $l_{\phi}$ の変化量は $\Delta l_{\phi} = {\rm R} \ \Delta \phi$ だから、

\cfrac{\mathrm{d} \phi}{\mathrm{d} y_{\rm p}} = \cfrac{\pi}{128\times 2^z} \ \cos\phi \ ,\ \ \
\cfrac{\mathrm{d} l_{\phi}}{\mathrm{d} y_{\rm p}} = \cfrac{\pi {\rm R}}{128 \times 2^z} \ \cos\phi

$\cfrac{\mathrm{d} l_{\lambda}}{\mathrm{d} x_{\rm p}} = \cfrac{\mathrm{d} l_{\phi}}{\mathrm{d} y_{\rm p}} $ より、メルカトル図法では局所的に緯線・経線方向を問わず縮尺が同じと分かります。さらに詳しく考えるとメルカトル図法の等角性より投影前後で図形の形が保存される（相似形になる）性質が分かりますが、本記事の範囲外のため省略します。

最適な zoom_level は？

緯度経度 $\phi_{\rm north},\phi_{\rm south}, \lambda_{\rm east}, \lambda_{\rm west}$ で定められる矩形範囲を考えます。表示の中心は矩形範囲の中心に合わせるとして、ちょうどのズームレベル $z$ は？

ピクセル座標と緯度・経度の関係式を使います。

\cfrac{\mathrm{d} x_{\rm p}}{\mathrm{d} \lambda} = \cfrac{128 \times 2^z}{\pi}, \ \cfrac{\mathrm{d} y_{\rm p}}{\mathrm{d} \phi} = \cfrac{128 \times 2^z}{\pi\ \cos\phi}

$\cos\phi$ の値に関しては、$\cos\left(\cfrac{\phi_{\rm north} + \phi_{\rm south}}{2} \right)$ で一定と見なせる程度に矩形範囲は十分狭いと仮定します。いま $W,H~[{\rm px}]$ の大きさ内部で地図を表示するなら、

\left\{
\begin{array}{l}
\cfrac{\mathrm{d} x_{\rm p}}{\mathrm{d} \lambda}\ \left( \lambda_{\rm east} - \lambda_{\rm west} \right) &\le& W \\
\cfrac{\mathrm{d} y_{\rm p}}{\mathrm{d} \phi} \left( \phi_{\rm north} - \phi_{\rm south}\right) &\le& H
\end{array}
\right.

を満たす最大のズームレベル $z$ を計算して、

z = \log_2 \left( \frac{\pi}{128}~\min \left\{ \cfrac{W}{\lambda_{\rm east} - \lambda_{\rm west}} , \frac{H~ \cos \left(\cfrac{\phi_{\rm north} + \phi_{\rm south}}{2} \right)}{\phi_{\rm north} - \phi_{\rm south}}\right\}\right) 

Maps JavaScript API を例に記述すれば、角度をオイラー角に直して、

map.ts

function moveToRect(
  rect: {south: number, north: number, west: number, east: number},
  element: HTMLElement,
  map: google.maps.Map,
){
  const bounds = element.getBoundingClientRect();
  const center = {
    lat: (rect.north + rect.south)/2,
    lng: (rect.east + rect.west)/2
  };
  const zoom_level = Math.floor(
    Math.log2( 
      360 / 256 * Math.min(
        bounds.width / (rect.north - rect.south), 
        bounds.height / (rect.east - rect.west) * Math.cos(center.lat * Math.PI / 180)
      )
    )
  );
  map.panTo(center);
  map.setZoom(zoom_level);
}  

zoom_level は整数値しか設定できないので、床関数で整数値に調整しています。