EAGLYSアドベントカレンダー19日目の記事です。
この記事は?
紛失通信の基本とモチベーションとその応用について解説した記事です!紛失通信は多人数での秘密計算(マルチパーティ計算)で頻出する道具でこれなしにマルチパーティ計算を語るのは不可能というくらいです!
紛失通信(Oblivious Transfer)とは?
Rabinによって考案された暗号技術の一つです。不思議な性質を持った通信で、以下の特徴を持ちます。
- 送信者は送った情報のうち、どれが届いたのか分からない
- 受信者は送られてきた情報のうち、一つの情報以外は得られない
この紛失通信は一見すると欠陥のあるプロトコルなのですが、複数人で通信するときに情報の非対称性を生み出すために利用されます。秘密情報(秘密鍵)を知っているかどうかで暗号文を解読できるかどうかが決まるので、複数人の通信で能動的に情報の非対称性を生み出せるのは強みといえるでしょう。
Exchange Of Secret(EOS)問題
Michael O. Rabin-How to Exchange Secrets with Oblivious Transfer May 20, 1981の論文
How to Exchange Secrets with Oblivious Transfer
を参考にOblivious Transferが必要な一例であるEOS問題を紹介します。ボブとアリスがある情報$S _ A$、$S _ B$を同時に交換したいとしましょう。
-
$S_A$はアリスの持っている秘密で、ボブの暗号化されたファイルを読むためのパスワード
-
$S_B$はボブの持っている秘密で、アリスの暗号化されたファイルを読むためのパスワード
-
暗号化されたファイルに間違ったパスワードを使うとファイルが破損するようになっている
この交換を愚直にやろうとするといくつか問題があります。
-
アリスがボブに$S_A$を渡した後にボブがアリスに送り返さずに逃げるかもしれない。
-
アリスがボブに誤った情報(例えば別データ$S$を$S_A$だと取り繕って)を送るかもしれない。
この問題を解決するためには、ボブもアリスもどちらも通信において優位に立てないようにする必要があります。これを第三者なしにやることは可能でしょうか?
EOSプロトコルの構成
そこでOblivious Transferが活躍します。このOblivious Transferの仕組みはRabin暗号を見るとわかりやすいと思います。
大きな素数$p,q$の積$n$は素因数分解が難しいものとします。暗号理論において、難しいということはできないのと同じ意味を持ちます。これを素因数分解仮定といいます。このプロトコルではパスワードを間違えると破損するので、パスワードを入手したことが確実なときだけアリスとボブはファイルを読もうとすることにします。
1 アリスは大きな素数$p_A$、$q_A$を選んで以下を計算して、それをボブに送る。
$$
n_A=p_A q_A
$$
同様にボブは以下を計算しアリスに送る。
$$
n_B=p_B q_B
$$
素因数分解仮定により、 $n_A$と$n_B$をそれぞれ素因数分解するのは難しい。
2 ボブは$n_A$以下の$x$をランダムに選び、以下を計算して$c$をアリスに送る。
$$
c=x^{2}\mod n _ {A}
$$
アリスは以下を計算して$x_1$を入手し、ボブに送る。
$$
x^{2} _ {1} =c\mod n_A\
$$
3 ボブはアリスから来た$n_A$,$x_1$と自分で作った$x$をもとに以下を計算する。
$$
gcd(x- x_1 ,n_A)=d
$$
このとき、ボブは2分の1の確率で$d=p_A$または$d=q_A$を入手し、xを素因数分解できる。アリスはボブのxを知らないし、ボブが素因数分解できたのかも分からない。
$$
v_B=\begin{cases}
0 & (success) \
1 & (otherwise)
\end{cases}
$$
ボブは$v_B$を定義する。この値はボブが素因数分解できた時に0になり、そうでない場合1になるような値である。$v_A$はボブをアリスとした場合の値である。以下を計算してこれをアリスに送る。
$$
\epsilon_B=S_B \oplus v_B
$$
アリスからはボブが素因数分解できたか分からず、$v_B$が0か1か分からないので$\epsilon_B$から$S_B$の情報は漏れない。
4 ここまでの処理をOblivious Transferと呼ぶ。これをアリスとボブを逆にして行う。
5 アリスはボブに対し、$E_{n_A}(m_A)=C=d_A$を送る。この$d_A$を復号するには、素因数$p_A,q_A$を知らないといけない。これをボブも$E_{n_B}(m_B)=d_B$を計算しに繰り返す。
EOS問題を解決できている?
5では$d_A$と$d_B$送り合っています。もしボブが$v_B=0$、つまり素因数分解できていたならボブは$d_A$から$S_A$と$m_A$が読めたことになるが、同時にアリス側では$v_B=0$であることになるので
$$
\epsilon_B=S_B \oplus 0 = S_B\
$$
となり$S_B$がアリスも$S_B$を入手した状態になる。
もし、ボブが素因数分解できていなかったなら
$$
\epsilon_B=S_B \oplus 1 \ne S_B\
$$
となり、アリスも$S_B$を持っていません。つまり、ボブが読めたら、アリスも読める状態になる。どちらもファイルを同時に読めるようになり、有利不利がないということになります。
なお、アリスに送られた$\epsilon_B$は3/4の確率で$\epsilon_B=S_B$です($\epsilon _ B=S _ B$じゃないのは$\epsilon _ B=0 \oplus 1 = 1$のときだけ)。しかし、前提条件より確実に$\epsilon_B=S_B$ではないのでアリスはファイルを読もうとしません。ボブがファイルを読んだという事実を知るか(ボブが通信中に逃げた場合)、$d_B$から$S_B$を読むまで(ボブが通信中に逃げなかった場合)ファイルを読みません。
このプロトコルはどちらも素因数分解成功、どちらかが失敗、どちらも失敗のパターンがありますが、どちらも失敗すると秘密が交換できません。この確率は1/4です。
1-out-of-2 紛失通信
スキーム
ここまでRabinの紛失通信を紹介しました。しかし、実際には紛失通信はk-out-of-nの形で用いられることが多いです。この紛失通信は
- ボブが$n$個の入力のうちどの$k$個を受信したか、アリスは分からない
- アリスが送った$n$個のうち、ボブは$k$個の情報しか分からない
ここでは岡本、山本先生による現代暗号を参考に1-out-of-2の例を一つ示します。(n=2,k=1)
- アリスは秘密鍵$sk$と公開鍵$pk$のペアを生成して、$pk$だけ送る。
- アリスは乱数$r_0,r_1\in_R Z_n$をボブに送る。
- ボブは$b\in_R\{0,1\}$と$x\in_R Z_n$を選ぶ。
- ボブは$q=Enc_{pk}(x)+r_b\bmod N$をアリスに送る。
- アリスは$y_i=Dec_{sk}(q-r_i \mod N)(b\in\{0,1\})$を計算する。
- アリスは以下の$c_0,c_1$を計算してボブに送る。
- ボブは$m_b=c_b-x\bmod n$を得る。
\begin{align*}
c_0&=m_0+y_0\\
c_1&=m_1+y_1
\end{align*}
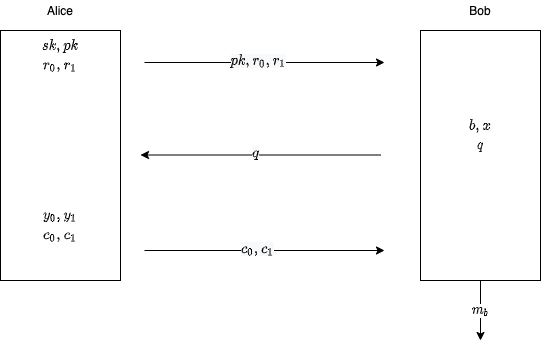
図に表すとこのような感じです。
$m_0$と$m_1$のうちどれかを得ています。これが2つのうち1つだけを手に入れる1-out-of-2です。
安全性
紛失通信が要件を満たしていて安全であることを確認します。満たすべき要件は以下の二つでした。(nとkには具体的な値を入れています)
- ボブが$2$個の入力のうちどの$1$個を受信したか、アリスは分からない
- アリスが送った$2$個のうち、ボブは$1$個の情報しか分からない
では安全か確認しましょう。選ばなかった$b$を$b\oplus 1$と表現します。アリスは本当に$m_0$と$m_1$のうち、どちらを選んだのかわからないのでしょうか?
まず、$q$の定義は
q = Enc_{pk}(x)+r_b \\
となります。$y_b$の定義は
y_b = Dec_{sk}(q-r_b\mod N)=Dec_{sk}(Enc_{pk}(x) + r_b - r_b\mod N)=x
より、ボブが選んだ$b$のときは、$y_b=x$ですが、$y_{b\oplus 1}$はただの乱数になります。しかし、アリスは$x$を知らないのでアリスからはどちらも乱数にしか見えず、見分けが付きません。アリスにはボブがどちらを選んだのかわからないということになります。
ボブは本当に$m_0$と$m_1$のうち、片方しか知ることができないのでしょうか?ボブは$c_b$と$x$を持っているので$m_b$を計算できますが、選ばなかった方の$b$は
c_{b\oplus 1}=m_{b\oplus 1} + y_{b\oplus 1}
の式と$y_{b\oplus 1}$がただの乱数であることから、$c_{b\oplus 1}$がただの乱数になることがわかります。では、ボブが$y_{b\oplus 1}$を計算して、
c_{b\oplus 1}-y_{b\oplus 1}=m_{b\oplus 1} + y_{b\oplus 1}-y_{b\oplus 1}
としたらどうでしょうか?これが成功すれば、$m_{b\oplus 1}$をボブが読めてしまいます。しかし、$y_{b\oplus 1}$を計算できません。なぜなら、計算するためには
y_{b\oplus 1}=Dec_{sk}(q-r_{b\oplus 1}\mod N)
を計算する必要があります。$q+r_{b\oplus 1}$はボブが知っている情報ですが、秘密鍵$sk$はボブが知らない情報です。ボブは公開鍵の一方向性により、$sk$なしに暗号文$q-r_{b\oplus 1}$から、それに対応する平文$y_{b\oplus 1}$を計算できません。
結局$m_{b\oplus1}$がただの乱数になってしまい、ボブはアリスが送った情報のうち一つしかわからないことになります。
紛失通信の応用
紛失通信を応用した手法について解説します。ここは応用的な内容になので、読み飛ばしていただいても構いません。
Oblivious Polynomial Evaluation
Oblivious Polynomial Evaluation(以下OPE)はOTを応用した手法で、
-
アリスとボブは多項式$P$を知っている。
-
$a$はアリスしか知らない
という状況でボブが$P(a)$を得るが$a$はわからないようなプロトコルです。私のブログの記事で解説しています。
Garbled Circuit
Garbled Circuitは1982年にYaoが提案した2者間の秘密計算プロトコルで、複数人での秘密計算の手法のなかでも重要な手法のひとつです。紛失通信を利用して、入力を秘密にしつつ関数を評価することを可能にしています。こちらも私のブログの記事で詳しく解説しています。
MASCOT
MASCOTは秘密計算プロトコルのひとつで、SPDZと同様に不正者が過半数以上でも安全であることを保証した手法です。SPDZとオンラインフェーズは同じなのですが、プリプロセスフェーズで紛失通信を活用して高速化することに成功しています。
まとめ
紛失通信は複数人間での秘密計算において重要な役割を果たしている技術なのですが、日本語では書籍が揃っていないように感じます。興味を持った方はぜひ原論文や参考文献にある本を読んでみてください!
参考文献
-
Oblivious Transfer How to Exchange Secrets with Oblivious Transfer
-
Garbled Circuit Protocols for Secure Computations,Andrew C. Yao,1982
-
岡本龍明、山本博資 現代暗号 (シリーズ・情報科学の数学) 1997 (筆者が知る限り、紛失通信が書かれている唯一の和書です)