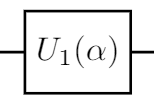今まで大学院で数学のトポロジーを学んできた者です．結び目理論に関する量子アルゴリズムや組みひも理論のアイデアが量子コンピュータに使われていることを学んだことがきっかけで，量子情報の分野に興味を持ち始めました．本記事ではIBM のPython ソフトウェア開発キットであるQISKit のシミュレータを使ってJones 多項式の量子アルゴリズムを簡単な具体例で実装することを試みます．初めての投稿で，量子情報については勉強し始めたばかりのため，誤り等ありましたら，ご指摘いただけると幸いです．
#目標
本記事の目標はQISKit を使って８の字結び目のJones 多項式の虚数単位$i = \sqrt{-1}$と$1$の原始5乗根$e^{\frac{2 \pi i}{5}}$での近似値を求めることです．Jones 多項式は結び目を分類するのに役立ったり，場の量子論との関係が見つかったりしたことから，大変興味深い研究対象になっています．特にJones 多項式の$1$の累乗根$e^{\frac{2 \pi i}{n}}$（$n$は自然数）での値は体積予想とよばれる長年の結び目理論の予想とも関連しています．Jones 多項式そのものを求める方法は色々と知られています．特にJones 多項式の$e^{\frac{2 \pi i}{n}}$（$n = 4, 5, 6, \cdots$）での値を直接求める方法として，量子計算を行う方法があります．以下８の字結び目の場合を例として，求め方を簡単に説明します．
８の字結び目は以下のように一本のひもを絡ませ両端をつなげた形で表わせます：
$\hspace{5.0cm}$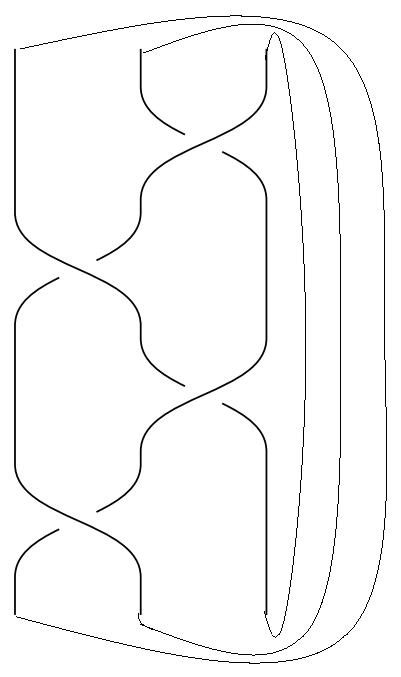
ここで交わり方を以下のように記号で表わすことにします：
$\hspace{5.0cm}$$\sigma_1 :=$
, $\hspace{1.0cm}$$\sigma_2 :=$
,
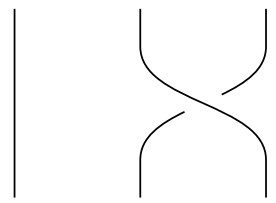また，上下を入れ替えた交わり方をそれぞれ$\sigma_1^{-1}$, $\sigma_2^{-1}$で表わすことにします：
$\hspace{4.5cm}$ $\begin{align} \sigma_1^{-1} := \end{align}$
, $\hspace{1.0cm}$ $\begin{align} \sigma_2^{-1} := \end{align}$
すると，８の字結び目は交わり方を上から下に順に見ることにより，$\sigma_2^{-1} \sigma_1 \sigma_2^{-1} \sigma_1$と表わすことができます．
次に$\sigma_1$, $\sigma_2$に対し，以下のようにユニタリ行列を対応させます：
$$\begin{align}
\sigma_1 &\mapsto
A_1 :=
e^{\frac{\pi i}{8}}
\begin{pmatrix}
1 & 0 \ \\
0 & -i
\end{pmatrix}, \\
\sigma_2 &\mapsto
A_2 :=
\frac{1}{\sqrt{2}} \begin{pmatrix}
e^{-\frac{\pi i}{8}} & e^{\frac{3 \pi i}{8}} \\
e^{\frac{3 \pi i}{8}} & e^{-\frac{\pi i}{8}}
\end{pmatrix}.
\end{align}$$
$\sigma_1^{-1}$, $\sigma_2^{-1}$に対してはそれぞれの逆行列，すなわち随伴行列$A_1^{\dagger}$, $A_2^{\dagger}$を対応させます．すると，$\sigma_2^{-1} \sigma_1 \sigma_2^{-1} \sigma_1$に対応する行列の積$A_2^{\dagger} A_1 A_2^{\dagger} A_1$のトレース，つまり$(1,1)$-成分と$(2,2)$-成分の和の値が８の字結び目のJones多項式の$i$での値$-1$になります$^{*1}$．
また，$\eta := 2 \cos\frac{\pi}{5} =\frac{1 + \sqrt{5}}{2}$とおくと，$\sigma_1$, $\sigma_2$に対し，
$$\begin{align}
\sigma_1 &\mapsto
B_1 :=
\begin{pmatrix}
e^{-\frac{4 \pi i}{5}} & 0 & 0\ \\
0 & e^{\frac{3 \pi i}{5}} & 0\ \
0 & 0 & e^{\frac{3 \pi i}{5}}
\end{pmatrix}, \\
\sigma_2 &\mapsto
B_2 :=
\begin{pmatrix}
\eta^{-1} e^{\frac{4 \pi i}{5}} & \eta^{-\frac{1}{2}} e^{-\frac{3 \pi i}{5}} & 0\ \\
\eta^{-\frac{1}{2}} e^{-\frac{3 \pi i}{5}} & -\eta^{-1} & 0\ \
0 & 0 & e^{\frac{3 \pi i}{5}}
\end{pmatrix}
\end{align}$$とユニタリ行列を対応させることを考えます．$\sigma_2^{-1} \sigma_1 \sigma_2^{-1} \sigma_1$に対応する行列の積$B_2^{\dagger} B_1 B_2^{\dagger} B_1$の$(i,j)$-成分を$b_{ij}$とおくと，
$$\begin{align} \eta^2 \cdot \frac{1}{\sin\frac{2 \pi}{5} + \sin\frac{2 \pi}{5} + \sin\frac{4 \pi}{5}} \cdot \left( \sin\frac{2 \pi}{5} \cdot b_{11} + \sin\frac{2 \pi}{5} \cdot b_{22} + \sin\frac{4 \pi}{5} \cdot b_{33} \right) \end{align}
$$の値が８の字結び目のJones多項式の$e^{\frac{2 \pi i}{5}}$での値$-\sqrt{5} + 1$になります$^{*1}$．
以上より，ユニタリ行列の積の対角成分が分かれば，Jones 多項式の$i$と$e^{\frac{2 \pi i}{5}}$での値を求めることができます．もちろん行列の積を直接計算すれば対角成分を求めることができますが，本記事ではHadamard テストとよばれる量子アルゴリズムを使って求めることを考えます．
$\ast 1$
８の字結び目のJones 多項式$J(q)$は$\begin{align} q^2 - q + 1 - q^{-1} + q^{-2} \end{align}$で与えられます．$q$に$i$と$\begin{align} e^{\frac{2 \pi i}{5}} \end{align}$を代入した値はそれぞれ以下のようになります： $$\begin{align} J(i) &= (- 1) - i + 1 - (-i) + (- 1) = -1 \\\ J\left(e^{\frac{2 \pi i}{5}} \right) &= \left(e^{\frac{4 \pi i}{5}} + e^{-\frac{4 \pi i}{5}} \right) + \left(e^{\frac{2 \pi i}{5}} + e^{-\frac{2 \pi i}{5}} \right) + 1 \\\ &= 2\cos\frac{4 \pi}{5} - 2\cos\frac{2 \pi}{5} + 1 \\\ &= 2 \cdot \left(-\frac{\sqrt{5} + 1}{4} \right) - 2 \cdot \frac{\sqrt{5} - 1}{4} + 1 \\\ &= -\sqrt{5} + 1. \end{align}$$#量子計算の準備
まず本記事で必要な量子計算の基礎について列挙します．
本記事では代表的なベクトルを以下のようにブラケット記法で定めます：
| ブラケット記法 | ベクトル |
|---|---|
| $\mid 0 \rangle$ | $\begin{pmatrix}1 \\ 0 \end{pmatrix}$ |
| $\mid 1 \rangle$ | $\begin{pmatrix}0 \\ 1 \end{pmatrix}$ |
| $\langle 0 \mid$ | $\begin{pmatrix} 1 & 0 \end{pmatrix}$ |
| $\langle 1 \mid$ | $\begin{pmatrix} 0 & 1 \end{pmatrix}$ |
$| \psi \rangle := \alpha | 0 \rangle + \beta | 1 \rangle = \begin{pmatrix}\alpha \\ \beta \end{pmatrix}$（$\alpha$, $\beta$は複素数）とおくと，$|\alpha|^2 + |\beta|^2 = 1$（$| \cdot |$は複素数の絶対値）を満たすとき，$| \psi \rangle$を量子ビットといいます．
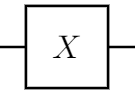
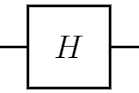
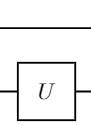
本記事で扱う一つの量子ビットに対する代表的な量子ゲートとして以下があります（$\alpha$は実数）：
| 量子ゲート | ユニタリ行列 | ブラケット記法 |
|---|---|---|
 |
$$\begin{pmatrix}0 & 1\\ 1 & 0 \end{pmatrix}$$ | $$\mid 1 \rangle \langle 0 \mid + \mid 0 \rangle \langle 1 \mid$$ |
 |
$$\begin{pmatrix} \frac{1}{\sqrt{2}} &\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}}\end{pmatrix}$$ | $$\frac{\mid 0 \rangle + \mid 1 \rangle}{\sqrt{2}}\langle 0 \mid + \frac{\mid 0 \rangle - \mid 1 \rangle}{\sqrt{2}}\langle 1 \mid$$ |
 |
$$\begin{pmatrix}1 & 0\\ 0 & i \end{pmatrix}^{\dagger} = \begin{pmatrix}1 & 0\\ 0 & -i \end{pmatrix}$$ | $$\mid 0 \rangle \langle 0 \mid - i \mid 1 \rangle \langle 1 \mid$$ |
 |
$$\begin{pmatrix}1 & 0\\ 0 & e^{i \alpha} \end{pmatrix}$$ | $$\mid 0 \rangle \langle 0 \mid + e^{i \alpha} \mid 1 \rangle \langle 1 \mid$$ |
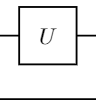
次に$U := \begin{pmatrix}a & b\\ c & d \end{pmatrix}$をユニタリ行列，$I := \begin{pmatrix}1 & 0\\ 0 & 1 \end{pmatrix}$を単位行列とします．二つの量子ビットに対する量子ゲートを行列ではテンソル積$\otimes$を使って表わします：
| 量子ゲート | ユニタリ行列 |
|---|---|
 |
$I \otimes U = \begin{pmatrix}a & b & 0 & 0 \\ c & d & 0 & 0 \\ 0 & 0 & a & b \\0 & 0 & c & d \end{pmatrix}$ |
 |
$U \otimes I = \begin{pmatrix}a & 0 & b & 0 \\ 0 & a & 0 & b \\ c & 0 & d & 0 \\0 & c & 0 & d \end{pmatrix}$ |
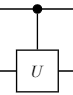
また，二つの量子ビットに対する代表的な量子ゲートとして以下の制御ゲートがあります．
| 量子ゲート | ユニタリ行列 | ブラケット記法 |
|---|---|---|
 $${\rm controlled}\text{-}U$$ |
$$\begin{pmatrix}I & O\\ O & U \end{pmatrix} = \begin{pmatrix}1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & a & b \\0 & 0 & c & d \end{pmatrix}$$ | $$\mid 0 \rangle \langle 0 \mid \otimes I + \mid 1 \rangle \langle 1 \mid \otimes U$$ |
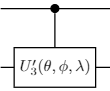
実はどんな${\rm controlled}\text{-}U$ も$U_1(\alpha)$ と以下の制御ゲート${\rm c}U_3(\theta, \phi, \lambda)$で表わすことができます．本記事では説明を見やすくするために，ユニタリ行列$\begin{pmatrix}
e^{i (-\frac{\phi + \lambda}{2})} \cos\frac{\theta}{2} & -e^{i (-\frac{\phi - \lambda}{2})} \sin\frac{\theta}{2} \
e^{i \cdot \frac{\phi - \lambda}{2}} \sin\frac{\theta}{2} & e^{i \cdot \frac{\phi + \lambda}{2}} \cos\frac{\theta}{2}
\end{pmatrix}$を$U_{3}^{\prime}(\theta, \phi, \lambda)$とおくことにします$^{\ast 2}$．
| 量子ゲート | ユニタリ行列 |
|---|---|
 $${\rm c}U_3(\theta, \phi, \lambda)$$ |
$$\begin{pmatrix}I & O\\ O & U_3^{\prime}(\theta, \phi, \lambda) \end{pmatrix} = \begin{pmatrix}1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & e^{i (-\frac{\phi + \lambda}{2})} \cos\frac{\theta}{2} & -e^{i (-\frac{\phi - \lambda}{2})} \sin\frac{\theta}{2} \\0 & 0 & e^{i \cdot \frac{\phi - \lambda}{2}} \sin\frac{\theta}{2} & e^{i \cdot \frac{\phi + \lambda}{2}} \cos\frac{\theta}{2} \end{pmatrix}$$ |
どんなユニタリ行列も，四つの実数$\alpha$, $\theta$, $\phi$, $\lambda$を使って，
$$\begin{align}
e^{i \alpha} \cdot U_{3}^{\prime}(\theta, \phi, \lambda) =
\begin{pmatrix}
e^{i \alpha} & 0 \
0 & e^{i \alpha}
\end{pmatrix}
U_{3}^{\prime}(\theta, \phi, \lambda)
\end{align}$$
と表わすことができます$^{\ast 3}$．よって，
$$\begin{align}
{\rm controlled}\text{-}\begin{pmatrix}
e^{i \alpha} & 0 \
0 & e^{i \alpha}
\end{pmatrix} = \begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & e^{i \alpha} & 0 \
0 & 0 & 0 & e^{i \alpha}
\end{pmatrix} = \begin{pmatrix}
1 \cdot I & 0 \
0 & e^{i \alpha} \cdot I
\end{pmatrix} = U_1(\alpha) \otimes I
\end{align}$$
より，以下の等式を得ることができます$^{\ast 4}$：
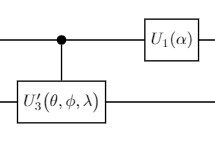
$$\begin{align} {\rm controlled}\text{-}U = (U_1(\alpha) \otimes I) \cdot {\rm c}U_3(\theta, \phi, \lambda). \end{align}$$
$\hspace{5cm}$ ${\Huge =}$ 
$\ast 2$
QISKit やIBM Q Experience で準備されている$U_3(\theta, \phi, \lambda) := \begin{pmatrix} \cos\frac{\theta}{2} & -e^{i \lambda} \sin\frac{\theta}{2}\\\e^{i \phi} \sin\frac{\theta}{2} & e^{i \cdot (\phi + \lambda)} \cos\frac{\theta}{2} \end{pmatrix}$とは一般には異なります．$U_{3}^{\prime}(\theta, \phi, \lambda) = e^{i (-\frac{\phi + \lambda}{2})} \cdot U_3(\theta, \phi, \lambda)$です．${\rm c}U_3(\theta, \phi, \lambda) = {\rm controlled}\text{-}U_3^{\prime}(\theta, \phi, \lambda)$と${\rm controlled}\text{-}U_3(\theta, \phi, \lambda)$も一般には異なります．$\ast 3$
$U = \begin{pmatrix} a & b \\\ c & d \end{pmatrix}$とおくと，$| \det(U) | = 1$, $U U^{\dagger} = I$より，$$\begin{align} a d - b c &= e^{i \alpha^{\prime}} \ (\alpha^{\prime} は実数) \tag{1} \\\ a \overline{c} + b \overline{d} &= 0 \tag{2} \\\ | c | + | d | &= 1 \tag{3} \end{align}$$が成り立ちます（$^{-}$は複素共役）．$(1) \times \overline{d} + (2) \times c$より， $$a(| c | + | d |) = \overline{d} e^{i \alpha^{\prime}}, $$$(1) \times \overline{c} + (2) \times d$より， $$-b(| c | + | d |) = \overline{c} e^{i \alpha^{\prime}} $$となるので，$(3)$より，$a = \overline{d} e^{i \alpha^{\prime}}$, $b = -\overline{c} e^{i \alpha^{\prime}}$が得られます．また，$(3)$より，$c = e^{i \varphi_1} \sin \frac{\theta}{2}$, $d = e^{i \varphi_2} \cos \frac{\theta}{2}$（$\varphi_1$, $\varphi_2$, $\theta$は実数）と表わせます．よって，$\alpha^{\prime} = 2 \alpha$, $\varphi_1 = \alpha + \frac{\phi - \lambda}{2}$, $\varphi_2 = \alpha + \frac{\phi + \lambda}{2}$とおくことにより， $$U = \begin{pmatrix} e^{i(\alpha^{\prime} - \varphi_2)} \cos\frac{\theta}{2} & -e^{i (\alpha^{\prime} - \varphi_1)} \sin \frac{\theta}{2} \\\ e^{i \varphi_1} \sin\frac{\theta}{2} & e^{i \varphi_2} \cos\frac{\theta}{2} \end{pmatrix} = e^{i \alpha} \begin{pmatrix} e^{i (-\frac{\phi + \lambda}{2})} \cos\frac{\theta}{2} & -e^{i (-\frac{\phi - \lambda}{2})} \sin\frac{\theta}{2} \\\ e^{i \cdot \frac{\phi - \lambda}{2}} \sin\frac{\theta}{2} & e^{i \cdot \frac{\phi + \lambda}{2}} \cos\frac{\theta}{2} \end{pmatrix} = \begin{pmatrix} e^{i \alpha} & 0 \\\ 0 & e^{i \alpha} \end{pmatrix} U_{3}^{\prime}(\theta, \phi, \lambda) $$と表わせます．$\ast 4$
実は$\begin{pmatrix} e^{i \alpha} & 0 \\\ 0 & e^{i \alpha} \end{pmatrix} U_{3}^{\prime}(\theta, \phi, \lambda) = U_{3}^{\prime}(\theta, \phi, \lambda) \begin{pmatrix} e^{i \alpha} & 0 \\\ 0 & e^{i \alpha} \end{pmatrix}$なので， $\hspace{5cm}$  ${\Huge =}$  とも表わせます．一般には二つのユニタリ行列$U_1$, $U_2$の積$U_1 U_2$を量子ゲートで表わすときは順序に注意する必要があります： $\hspace{5cm}$ ${\Huge =}$ 最後に本記事での測定について説明します．量子ビット$| \psi \rangle = \alpha | 0 \rangle + \beta | 1 \rangle = \begin{pmatrix}\alpha \\ \beta \end{pmatrix}$に対し，測定したとき$| 0 \rangle$が出力される確率を$| \alpha |^2$と定義します．この確率はベクトルの大きさ$| | \cdot | |$と行列$P_0 := | 0 \rangle \langle 0 | = \begin{pmatrix}1 & 0\\ 0 & 0 \end{pmatrix}$を使って，$| | P_0 \cdot | \psi \rangle | |^2$でも計算されます．このことにならって，二つの量子ビット$| \psi_1 \rangle \otimes$ $| \psi_2 \rangle$に対し，一つ目（左）の量子ビットだけを測定したとき$| 0 \rangle$が出力される確率は$| | (P_0 \otimes I) \cdot (| \psi_1 \rangle \otimes | \psi_2 \rangle) | |^2$で計算されます．本記事ではこの測定を
で表わすことにします．
#Hadamard テスト
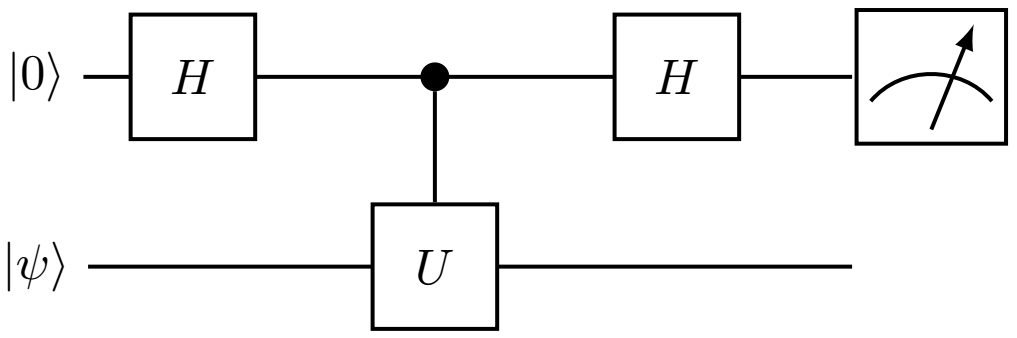
次にHadamard テストについて説明します．Hadamard テストは行列の対角成分の実部・虚部を求める二種類があります．$| \psi \rangle =$ $| 0 \rangle$または$| 1 \rangle$とすると，ユニタリ行列$U$の対角成分の実部を求めるHadamard テストの量子回路は以下のようになります：
$\hspace{5.0cm}$
測定直前の状態を計算すると，$\langle 0| 0 \rangle = 1$, $\langle 0| 1 \rangle = 0$より，
$$
\begin{align}
| 0 \rangle \otimes | \psi \rangle &\stackrel{H \otimes I}{\longmapsto} \frac{| 0 \rangle + | 1 \rangle}{\sqrt{2}} \otimes | \psi \rangle \\
& \hspace{-0.5cm} \stackrel{{\rm controlled}\text{-}U}{\longmapsto} \frac{1}{\sqrt{2}}(| 0 \rangle \otimes | \psi \rangle + | 1 \rangle \otimes U | \psi \rangle) \\
&\stackrel{H \otimes I}{\longmapsto} \frac{1}{2}((| 0 \rangle + | 1 \rangle) \otimes | \psi \rangle + (| 0 \rangle - | 1 \rangle) \otimes U | \psi \rangle) \\
&= \frac{1}{2} (|0 \rangle \otimes (I+U) |\psi \rangle + |1 \rangle \otimes (I-U) |\psi) \rangle )
\end{align}
$$になります．ここで，一つ目（上）の量子ビットを測定したとき測定したとき$| 0 \rangle$を出力する確率を$p_{0, | \psi \rangle, {\rm Re}}$とします．$U$はユニタリ行列より，$(U + U^{\dagger})$の対角成分 $= 2 \cdot$（$U$の対角成分の実部）になることに注意すると，
$$
\begin{align}
p_{0, | \psi \rangle, {\rm Re}} &=
\left| \left| (P_0 \otimes I) \cdot \left( \frac{1}{2} (|0 \rangle \otimes (I+U) |\psi \rangle + |1 \rangle \otimes (I-U) |\psi ) \rangle \right) \right| \right|^2 \\
&= \left| \left| \frac{1}{2} (|0 \rangle \otimes (I+U) |\psi \rangle ) \right| \right|^2 \
&= \left| \left| \frac{1}{2} \begin{pmatrix} 1 \cdot (I+U) |\psi \rangle \\ 0 \cdot (I+U) |\psi \rangle \end{pmatrix}
\right| \right|^2 \
&= \left| \left| \frac{1}{2} (I+U) |\psi \rangle \right| \right|^2 \
&= \frac{1}{4} \langle \psi | (I+U)^{\dagger} (I+U) |\psi \rangle \\
&= \frac{1}{4} \langle \psi | (I+U^{\dagger} ) (I+U) |\psi \rangle \\
&= \frac{1}{4} \langle \psi | (2I+ (U + U^{\dagger})) |\psi \rangle \\
&= \frac{1}{2} \bigl(1 + {\rm Re}(\langle \psi | U | \psi \rangle) \bigr)
\end{align}
$$となるので，${\rm Re}(\langle \psi | U | \psi \rangle) = 2p_{0, | \psi \rangle, {\rm Re}} -1$より，
$\hspace{5.0cm}$ $U$の$(1,1)$-成分の実部$= 2 p_{0, | 0 \rangle, {\rm Re}} -1$,
$\hspace{5.0cm}$ $U$の$(2,2)$-成分の実部$= 2 p_{0, | 1 \rangle, {\rm Re}} -1$
が得られます．
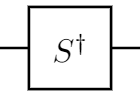
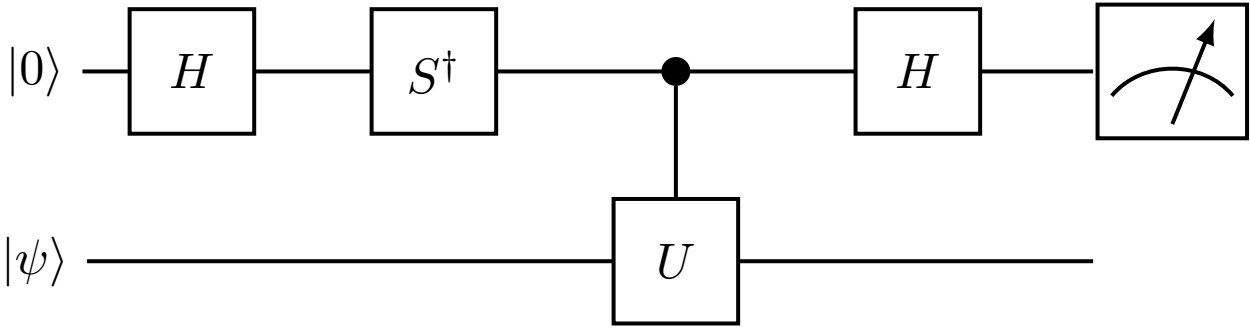
ユニタリ行列$U$の対角成分の虚部を求めるHadamard テストの量子回路は以下のようになります：
$\hspace{4.0cm}$
この場合の一つ目（上）の量子ビットを測定したとき$| 0 \rangle$を出力する確率を$p_{0, | \psi \rangle, {\rm Im}}$とします．同様に計算することによって$^{\ast 5}$，
$\hspace{5.0cm}$ $U$の$(1,1)$-成分の虚部$= 2 p_{0, | 0 \rangle, {\rm Im}} -1$,
$\hspace{5.0cm}$ $U$の$(2,2)$-成分の虚部$= 2 p_{0, | 1 \rangle, {\rm Im}} -1$
が得られます．
$\ast 5$
この場合の測定直前の状態は以下のようになります： $$ \begin{align} | 0 \rangle \otimes | \psi \rangle &\stackrel{H \otimes I}{\longmapsto} \frac{| 0 \rangle + | 1 \rangle}{\sqrt{2}} \otimes | \psi \rangle \\\ &\stackrel{S^{\dagger} \otimes I}{\longmapsto} \frac{| 0 \rangle - i | 1 \rangle}{\sqrt{2}} \otimes | \psi \rangle \\\ & \hspace{-0.5cm} \stackrel{{\rm controlled}\text{-}U}{\longmapsto} \frac{1}{\sqrt{2}}(| 0 \rangle \otimes | \psi \rangle - i | 1 \rangle \otimes U | \psi \rangle) \\\ &\stackrel{H \otimes I}{\longmapsto} \frac{1}{2}((| 0 \rangle + | 1 \rangle) \otimes | \psi \rangle - i (| 0 \rangle - | 1 \rangle) \otimes U | \psi \rangle) \\\ &= \frac{1}{2} (|0 \rangle \otimes (I - iU) |\psi \rangle + |1 \rangle \otimes (I + iU) |\psi \rangle ). \end{align} $$よって，$U$はユニタリ行列より，$(U - U^{\dagger})$の対角成分 $= 2 \cdot (U$の対角成分の虚部$) \cdot i $になることに注意すると， $$ \begin{align} p_{0, | \psi \rangle, {\rm Im}} &= \left| \left| (P_0 \otimes I) \cdot \left( \frac{1}{2} (|0 \rangle \otimes (I - iU) |\psi \rangle + |1 \rangle \otimes (I + iU) |\psi \rangle ) \right) \right| \right|^2 \\\ &= \left| \left| \frac{1}{2} (|0 \rangle \otimes (I - iU) |\psi \rangle ) \right| \right|^2 \\\ &= \left| \left| \frac{1}{2} \begin{pmatrix} 1 \cdot (I - iU) |\psi \rangle \\\ 0 \cdot (I - iU) |\psi \rangle \end{pmatrix} \right| \right|^2 \\\ &= \left| \left| \frac{1}{2} (I-iU) |\psi \rangle \right| \right|^2 \\\ &= \frac{1}{4} \langle \psi | (I-iU)^{\dagger} (I-iU) |\psi \rangle \\\ &= \frac{1}{4} \langle \psi | (I+iU^{\dagger}) (I-iU) |\psi \rangle \\\ &= \frac{1}{4} \langle \psi | (2I - i(U - U^{\dagger})) |\psi \rangle \\\ &= \frac{1}{2}\bigl(1 - i^2 \cdot {\rm Im}(\langle \psi | U | \psi \rangle) \bigr) \\\ &= \frac{1}{2}\bigl(1 + {\rm Im}(\langle \psi | U | \psi \rangle) \bigr) \end{align} $$となるので，${\rm Im}(\langle \psi | U | \psi \rangle) = 2 p_{0, | \psi \rangle, {\rm Im}} -1$が得られます．#８の字結び目のJones 多項式の虚数単位での近似値を求める
以上より準備が整ったので，８の字結び目のJones 多項式の虚数単位$i$での近似値をQISKit のシミュレータを使って求めてみます．
改めて目標を述べると，ユニタリ行列
$$\begin{align}
A_1 :=
e^{\frac{\pi i}{8}}
\begin{pmatrix}
1 & 0 \ \\
0 & -i
\end{pmatrix}, \
A_2 :=
\frac{1}{\sqrt{2}} \begin{pmatrix}
e^{-\frac{\pi i}{8}} & e^{\frac{3 \pi i}{8}} \\
e^{\frac{3 \pi i}{8}} & e^{-\frac{\pi i}{8}}
\end{pmatrix}.
\end{align}$$
に対し，行列の積$A_2^{\dagger} A_1 A_2^{\dagger} A_1$のトレースが$-1$と近似していることを確かめます．
QISKit では$U_1(\alpha)$と${\rm c}U_3(\theta, \phi, \lambda)$がすでに準備されています．そのため，一つのユニタリ行列に対し，四つの実数$\alpha$, $\theta$, $\phi$, $\lambda$を求めればよいことになります．
まず，ユニタリ行列$A_1$と$A_2$は以下のように表わされます：
$$\begin{align}
A_1 &= e^{\frac{\pi i}{8}} \begin{pmatrix}
e^{0 \cdot \pi i} & 0 \\
0 & e^{-\frac{\pi i}{2}}
\end{pmatrix} = e^{-\frac{\pi i}{8}} \begin{pmatrix}
e^{\frac{\pi i}{4}} & 0 \\
0 & e^{-\frac{\pi i}{4}}
\end{pmatrix} = e^{-\frac{\pi i}{8}} \begin{pmatrix}
e^{i \cdot (-\frac{1}{2} (-\frac{\pi}{2} + 0) )} \cos0 & -e^{i \cdot (-\frac{1}{2} (-\frac{\pi}{2} - 0) )} \sin0 \\
e^{i \cdot \frac{1}{2} (-\frac{\pi}{2} - 0) } \sin0 & e^{i \cdot \frac{1}{2} (-\frac{\pi}{2} + 0) } \cos0
\end{pmatrix}, \\
A_2 &= e^{-\frac{\pi i}{8}} \begin{pmatrix}
e^{0 \cdot \pi i} \cdot \frac{1}{\sqrt{2}} & e^{\frac{\pi i}{2}} \cdot \frac{1}{\sqrt{2}} \\
e^{\frac{\pi i}{2}} \cdot \frac{1}{\sqrt{2}} & e^{0 \cdot \pi i} \cdot \frac{1}{\sqrt{2}}
\end{pmatrix} = e^{-\frac{\pi i}{8}} \begin{pmatrix}
e^{i \cdot (-\frac{1}{2} (\frac{\pi}{2} - \frac{\pi}{2}) )} \cos(\frac{1}{2} \cdot \frac{\pi}{2}) & -e^{i \cdot (-\frac{1}{2} (\frac{\pi}{2} + \frac{\pi}{2}) )} \sin(\frac{1}{2} \cdot \frac{\pi}{2}) \\
e^{i \cdot \frac{1}{2} (\frac{\pi}{2} + \frac{\pi}{2}) } \sin(\frac{1}{2} \cdot \frac{\pi}{2}) & e^{i \cdot \frac{1}{2} (\frac{\pi}{2} - \frac{\pi}{2}) } \cos(\frac{1}{2} \cdot \frac{\pi}{2})
\end{pmatrix}.
\end{align}$$
$\overline{e^{i \varphi}} = e^{-i \varphi}$（$\varphi$は実数，$^{-}$は複素共役）より，$A_2^{\dagger}$は以下のように表わされます：
$$\begin{align}
A_2^{\dagger} = e^{\frac{\pi i}{8}} \begin{pmatrix}
e^{i \cdot (-\frac{1}{2} (-\frac{\pi}{2} + \frac{\pi}{2}) )} \cos(\frac{1}{2} \cdot \frac{\pi}{2}) & -e^{i \cdot (-\frac{1}{2} (-\frac{\pi}{2} - \frac{\pi}{2}) )} \sin(\frac{1}{2} \cdot \frac{\pi}{2}) \\
e^{i \cdot \frac{1}{2} (-\frac{\pi}{2} - \frac{\pi}{2}) } \sin(\frac{1}{2} \cdot \frac{\pi}{2}) & e^{i \cdot \frac{1}{2} (-\frac{\pi}{2} + \frac{\pi}{2}) } \cos(\frac{1}{2} \cdot \frac{\pi}{2})
\end{pmatrix}.
\end{align}$$
よって，$A_1$と$A_2^{\dagger}$の制御ゲートは$U_1(\alpha)$と${\rm c}U_3(\theta, \phi, \lambda)$を使って，以下のように表わされます：
$$\begin{align}
{\rm controlled}\text{-}A_1 &= \Bigl(U_1 \Bigl(-\frac{\pi}{8} \Bigr) \otimes I_2 \Bigr) \cdot {\rm c}U_3 \Bigl(0, -\frac{\pi}{2}, 0 \Bigr) \
{\rm controlled}\text{-}A_2^{\dagger} &= \Bigl(U_1 \Bigl(\frac{\pi}{8} \Bigr) \otimes I_2 \Bigr) \cdot {\rm c}U_3 \Bigl(\frac{\pi}{2}, -\frac{\pi}{2}, \frac{\pi}{2} \Bigr)
\end{align}$$
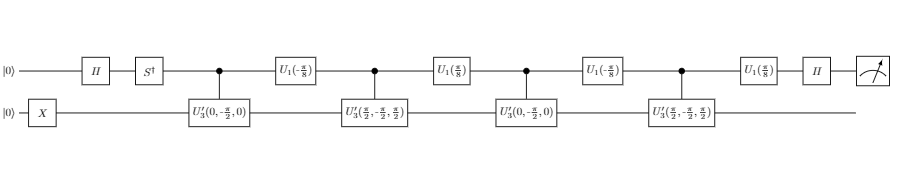
したがって，$A_2^{\dagger} A_1 A_2^{\dagger} A_1$の(1,1)-成分の実部・虚部を求めるHadamard テスト はそれぞれ以下のようになります（順序に注意）：
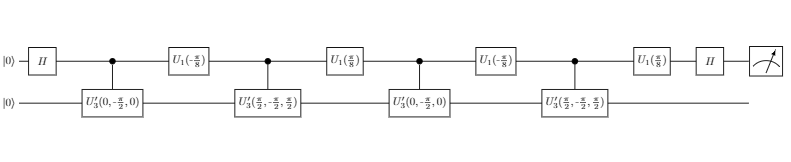
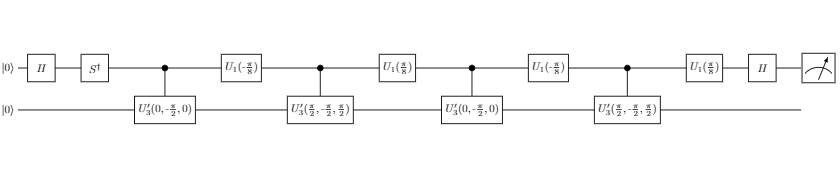
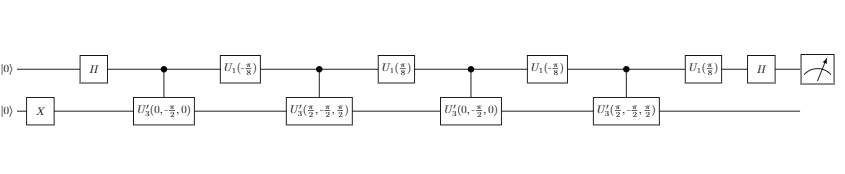
また，$X | 0 \rangle = | 1 \rangle$より, $A_2^{\dagger} A_1 A_2^{\dagger} A_1$の(2,2)-成分の実部・虚部を求めるHadamard テストはそれぞれ以下のように表わせます：
以上をQISKitを使って順番にまとめて書くと以下のようになります（本記事ではショット数（試行数，確率の分母）をデフォルト値の$1024$の場合で考えてみます）：
# numpy ver.1.14.5
# qiskit ver.0.5.7
from numpy import pi
import qiskit
from qiskit.tools.visualization import plot_histogram
alpha = {1: -pi/8, 2: pi/8}
theta = {1: 0, 2: pi/2}
phi = {1: -pi/2, 2: -pi/2}
lam = {1: 0, 2: pi/2}
qr = qiskit.QuantumRegister("qr", 2)
cr = qiskit.ClassicalRegister("cr", 1)
for j in range(4):
qc = qiskit.QuantumCircuit(qr, cr)
if j // 2 == 1:
qc.x(qr[1])
qc.h(qr[0])
if j % 2 == 1:
qc.sdg(qr[0])
qc.cu3(theta[1], phi[1], lam[1], qr[0], qr[1])
qc.u1(alpha[1], qr[0])
qc.cu3(theta[2], phi[2],lam[2], qr[0], qr[1])
qc.u1(alpha[2], qr[0])
qc.cu3(theta[1], phi[1], lam[1], qr[0], qr[1])
qc.u1(alpha[1], qr[0])
qc.cu3(theta[2], phi[2],lam[2], qr[0], qr[1])
qc.u1(alpha[2], qr[0])
qc.h(qr[0])
qc.measure(qr[0], cr[0])
qp = qiskit.QuantumProgram()
qp.add_circuit("Jones_fig8_4th", qc)
sim_result = qp.execute("Jones_fig8_4th", backend="local_qasm_simulator", shots=1024)
print("simulation: ", sim_result)
print(sim_result.get_counts("Jones_fig8_4th"))
plot_histogram(sim_result.get_counts("Jones_fig8_4th"))
```
```:結果
simulation: COMPLETED
{'0': 254, '1': 770}
```
$\hspace{3cm}$ 
```
simulation: COMPLETED
{'0': 785, '1': 239}
```
$\hspace{3cm}$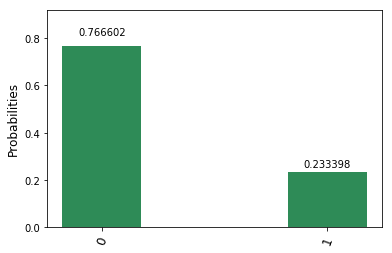 
```
simulation: COMPLETED
{'0': 258, '1': 766}
```
$\hspace{3cm}$ 
```
simulation: COMPLETED
{'0': 265, '1': 759}
```
$\hspace{3cm}$ 
以上の計４回の結果は実行するたびに多少変わります．そのため，本記事では上の操作を$1000$回繰り返し，得られたすべての確率の結果の平均をとることを考えます．すると，$A_2^{\dagger} A_1 A_2^{\dagger} A_1$のトレースの近似値は以下のようにして求まります：
```python:Jones_fig8_4th_1000.py
# numpy ver.1.14.5
# qiskit ver.0.5.7
from numpy import pi, mean
import qiskit
alpha = {1: -pi/8, 2: pi/8}
theta = {1: 0, 2: pi/2}
phi = {1: -pi/2, 2: -pi/2}
lam = {1: 0, 2: pi/2}
qr = qiskit.QuantumRegister("qr", 2)
cr = qiskit.ClassicalRegister("cr", 1)
N = 1000 # number of iterations
p0 = ["p_{0,0,Re}", "p_{0,0,Im}", "p_{0,1,Re}", "p_{0,1,Im}"] # list of probabilities
Re1 = [''] * N # list of Re of (1,1)
Im1 = [''] * N # list of Im of (1,1)
Re2 = [''] * N # list of Re of (2,2)
Im2 = [''] * N # list of Im of (2,2)
for i in range(N):
for j in range(4):
qc = qiskit.QuantumCircuit(qr, cr)
if j // 2 == 1:
qc.x(qr[1])
qc.h(qr[0])
if j % 2 == 1:
qc.sdg(qr[0])
qc.cu3(theta[1], phi[1], lam[1], qr[0], qr[1])
qc.u1(alpha[1], qr[0])
qc.cu3(theta[2], phi[2],lam[2], qr[0], qr[1])
qc.u1(alpha[2], qr[0])
qc.cu3(theta[1], phi[1], lam[1], qr[0], qr[1])
qc.u1(alpha[1], qr[0])
qc.cu3(theta[2], phi[2],lam[2], qr[0], qr[1])
qc.u1(alpha[2], qr[0])
qc.h(qr[0])
qc.measure(qr[0], cr[0])
qp = qiskit.QuantumProgram()
qp.add_circuit("Jones_fig8_4th", qc)
sim_result = qp.execute("Jones_fig8_4th", backend="local_qasm_simulator", shots=1024)
p0[j] = sim_result.get_counts("Jones_fig8_4th")['0'] / 1024
Re1[i] = 2 * p0[0] - 1
Im1[i] = 2 * p0[1] - 1
Re2[i] = 2 * p0[2] - 1
Im2[i] = 2 * p0[3] - 1
m_Re1 = mean(Re1)
m_Im1 = mean(Im1)
m_Re2 = mean(Re2)
m_Im2 = mean(Im2)
print("Re: ", m_Re1 + m_Re2)
print("Im: ", m_Im1 + m_Im2)
```
```:結果
Re: -0.999154296875
Im: -0.0015058593750000293
```
以上より，$A_2^{\dagger} A_1 A_2^{\dagger} A_1$のトレースは８の字結び目のJones多項式の$i$での値$-1 + 0 \cdot i$に近い値を得られることが確認できました．
#８の字結び目のJones 多項式の1の原始5乗根での近似値を求めることを試みる
最後に８の字結び目のJones 多項式の1の原始5乗根$e^{\frac{2 \pi i}{5}}$での近似値を前節と同様の方法で求めることを試みます．$\begin{align} \eta := 2 \cos\frac{\pi}{5}= \frac{1 + \sqrt{5}}{2} \end{align}$とおくと，目標は
$$\begin{align}
B_1 :=
\begin{pmatrix}
e^{-\frac{4 \pi i}{5}} & 0 & 0\ \\\
0 & e^{\frac{3 \pi i}{5}} & 0\ \\\
0 & 0 & e^{\frac{3 \pi i}{5}}
\end{pmatrix}, \
B_2 :=
\begin{pmatrix}
\eta^{-1} e^{\frac{4 \pi i}{5}} & \eta^{-\frac{1}{2}} e^{-\frac{3 \pi i}{5}} & 0\ \\\
\eta^{-\frac{1}{2}} e^{-\frac{3 \pi i}{5}} & -\eta^{-1} & 0\ \\\
0 & 0 & e^{\frac{3 \pi i}{5}}
\end{pmatrix}
\end{align}$$に対し，行列の積$B_2^{\dagger} B_1 B_2^{\dagger} B_1$の対角成分$b_{ii}$で表わされる値
$$\begin{align} \eta^2 \cdot \frac{1}{\sin\frac{2 \pi}{5} + \sin\frac{2 \pi}{5} + \sin\frac{4 \pi}{5}} \cdot \left( \sin\frac{2 \pi}{5} \cdot b_{11} + \sin\frac{2 \pi}{5} \cdot b_{22} + \sin\frac{4 \pi}{5} \cdot b_{33} \right) \end{align}
$$を求めることです．
まず$B_2^{\dagger} B_1 B_2^{\dagger} B_1$の$(3,3)$-成分$b_{33}$については直接計算することにより，$\begin{align} \overline{e^{\frac{3 \pi i}{5}}} \cdot e^{\frac{3 \pi i}{5}} \cdot \overline{e^{\frac{3 \pi i}{5}}} \cdot e^{\frac{3 \pi i}{5}} = e^{-\frac{3 \pi i}{5}} \cdot e^{\frac{3 \pi i}{5}} \cdot e^{-\frac{3 \pi i}{5}} \cdot e^{\frac{3 \pi i}{5}} = 1 \end{align}$になることが分かります．残りの$(1,1)$-成分$b_{11}$，$(2,2)$-成分$b_{22}$を求めるためには，$B_1$，$B_2$から第3行と第3列を取り除いた以下の二つの2行2列のユニタリ行列を考えます：
$$\begin{align}
B_1^{\prime} :=
\begin{pmatrix}
e^{-\frac{4 \pi i}{5}} & 0\ \\\
0 & e^{\frac{3 \pi i}{5}}
\end{pmatrix}, \
B_2^{\prime} :=
\begin{pmatrix}
\eta^{-1} e^{\frac{4 \pi i}{5}} & \eta^{-\frac{1}{2}} e^{-\frac{3 \pi i}{5}}\ \\\
\eta^{-\frac{1}{2}} e^{-\frac{3 \pi i}{5}} & -\eta^{-1}
\end{pmatrix}.
\end{align}
$$
行列の積${B_2^{\prime}}^{\dagger} B_1^{\prime} {B_2^{\prime}}^{\dagger} B_1^{\prime}$の$(1,1)$-成分，$(2,2)$-成分がそれぞれ$b_{11}$，$b_{22}$になります．よって，$B_1^{\prime}$と$B_2^{\prime}$に対する四つの実数$\alpha$, $\theta$, $\phi$, $\lambda$を求めます（$-\frac{3 \pi}{2} = \frac{\pi}{2} \ {\rm mod} \ 2 \pi$に注意）：
$$\begin{align}
B_1^{\prime} &= e^{-\frac{\pi i}{10}} \begin{pmatrix}
e^{-\frac{7 \pi i}{10}} & 0 \\\
0 & e^{\frac{7 \pi i}{10}}
\end{pmatrix} = e^{-\frac{\pi i}{10}} \begin{pmatrix}
e^{i \cdot (-\frac{1}{2} (\frac{7 \pi}{5} + 0) )} \cos0 & -e^{i \cdot (-\frac{1}{2} (\frac{7 \pi}{5} - 0) )} \sin0 \\\
e^{i \cdot \frac{1}{2} (\frac{7 \pi}{5} - 0) } \sin0 & e^{i \cdot \frac{1}{2} (\frac{7 \pi}{5} + 0) } \cos0
\end{pmatrix} \\\
B_2^{\prime} &= e^{\frac{9 \pi i}{10}} \begin{pmatrix}
e^{-\frac{\pi i}{10}} \cdot \eta^{-1} & e^{-\frac{3 \pi i}{2}} \cdot \eta^{-\frac{1}{2}} \\\
e^{-\frac{3 \pi i}{2}} \cdot \eta^{-\frac{1}{2}} & e^{\frac{\pi i}{10}} \cdot \eta^{-1}
\end{pmatrix} = e^{\frac{9 \pi i}{10}} \begin{pmatrix}
e^{i \cdot (-\frac{1}{2} (\frac{3 \pi}{5} - \frac{2 \pi}{5})) } \cdot \eta^{-1} & -e^{i \cdot (-\frac{1}{2} (\frac{3 \pi}{5} + \frac{2 \pi}{5}) )} \cdot \eta^{-\frac{1}{2}} \\\
e^{i \cdot \frac{1}{2} (\frac{3 \pi}{5} + \frac{2 \pi}{5}) } \cdot \eta^{-\frac{1}{2}} & e^{i \cdot \frac{1}{2} (\frac{3 \pi}{5} - \frac{2 \pi}{5}) } \cdot \eta^{-1}
\end{pmatrix}.
\end{align}$$
ここでは，$\eta^{-1} = \frac{\sqrt{5} - 1}{2} = 0.618 \cdots \approx \cos 51.8^{\circ} = \cos\left(\frac{1}{2} \cdot \frac{103.6 \pi}{180}\right)$と$\eta^{-\frac{1}{2}} \approx \sin 51.8^{\circ} = \sin\left(\frac{1}{2} \cdot \frac{103.6 \pi}{180}\right)$の近似値を使うことにします．すると，$B_1^{\prime}$と$B_2^{\prime}$の制御ゲートはそれぞれ以下のように表わされます：
$$\begin{align}
{\rm controlled}\text{-}B_1^{\prime} &= \left(U_1 \left(-\frac{\pi}{10} \right) \otimes I_2 \right) \cdot {\rm c}U_3 \left(0, \frac{7}{5}\pi, 0 \right)，\\\
{\rm controlled}\text{-}B_2^{\prime} &\approx \left(U_1 \left(\frac{9 \pi}{10} \right) \otimes I_2 \right) \cdot {\rm c}U_3 \left( \frac{103.6 \pi}{180}, \frac{3 \pi}{5}, -\frac{2 \pi}{5} \right)．
\end{align}
$$
実は量子ゲートの合成と逆行列に対する量子ゲートもQISKit を使って書くことができます．以上より，目標をまとめて書くと以下のようになります：
```python:Jones_fig8_5th_1000.py
# numpy ver.1.14.5
# qiskit ver.0.5.7
from numpy import pi, mean, sin, cos
import qiskit
from qiskit.extensions.standard.cu3 import Cu3Gate
from qiskit.extensions.standard.u1 import U1Gate
alpha = {1: -pi/10, 2: -9*pi/10}
theta = {1: 0, 2: 103.6*pi/180}
phi = {1: 7*pi/5, 2: -3*pi/5}
lam = {1: 0, 2: 2*pi/5}
qr = qiskit.QuantumRegister("qr", 2)
cr = qiskit.ClassicalRegister("cr", 1)
Cb = {1: "Controlled-b_1", 2: "Controlled-b_2"}
Cbdg = {1: "Controlled-b_1^dg", 2: "Controlled-b_2^dg"}
for k in range(1,3):
Cb[k] = qiskit.CompositeGate('', [], [qr[0], qr[1]])
Cb[k]._attach(Cu3Gate(theta[k], phi[k], lam[k], qr[0], qr[1]))
Cb[k]._attach(U1Gate(alpha[k], qr[0]))
Cbdg[k] = Cb[k].inverse()
N = 1000 # number of iterations
p0 = ["p_{0,0,Re}", "p_{0,0,Im}", "p_{0,1,Re}", "p_{0,1,Im}"] # list of probabilities
Re1 = [''] * N # list of Re of (1,1)
Im1 = [''] * N # list of Im of (1,1)
Re2 = [''] * N # list of Re of (2,2)
Im2 = [''] * N # list of Im of (2,2)
for i in range(N):
for j in range(4):
qc = qiskit.QuantumCircuit(qr, cr)
if j // 2 == 1:
qc.x(qr[1])
qc.h(qr[0])
if j % 2 == 1:
qc.sdg(qr[0])
qc._attach(Cb[1])
qc._attach(Cbdg[2])
qc._attach(Cb[1])
qc._attach(Cbdg[2])
qc.h(qr[0])
qc.measure(qr[0], cr[0])
qp = qiskit.QuantumProgram()
qp.add_circuit("Jones_fig8_5th", qc)
sim_result = qp.execute("Jones_fig8_5th", backend="local_qasm_simulator", shots=1024)
p0[j] = sim_result.get_counts("Jones_fig8_5th")['0'] / 1024
Re1[i] = 2 * p0[0] - 1
Im1[i] = 2 * p0[1] - 1
Re2[i] = 2 * p0[2] - 1
Im2[i] = 2 * p0[3] - 1
m_Re1 = mean(Re1)
m_Im1 = mean(Im1)
m_Re2 = mean(Re2)
m_Im2 = mean(Im2)
eta = 2 * cos(pi/5)
s2 = sin(2*pi/5)
s4 = sin(4*pi/5)
print("Re: ", eta ** 2 * 1/(s2 + s2 + s4) * (s2 * m_Re1 + s2 * m_Re2 + s4 * 1))
print("Im: ", eta ** 2 * 1/(s2 + s2 + s4) * (s2 * m_Im1 + s2 * m_Im2))
```
```:結果
Re: -1.2362804643751049
Im: 0.001255859375000018
```
以上より，８の字結び目のJones 多項式の$e^{\frac{2 \pi i}{5}}$での値$\begin{align} -\sqrt{5} + 1 + 0 \cdot i = -1.23606 \cdots \end{align}$と近い値を得ることができました．
####参考文献
・D. Aharonov, V. Jones, and Z. Landau, A polynomial quantum algorithm for approximating the Jones polynomial, arXiv:quant-ph/0511096v2.
・B. Field and T. Simula, Introduction to topological quantum computation with non-Abelian anyons, arXiv:quant-ph/1802.06176v2.
・M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information: 10th Anniversary Edition, Cambridge University Press (2010).