はじめに
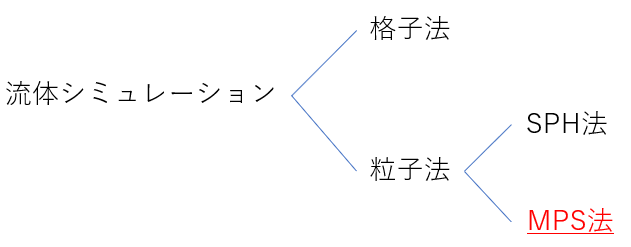
一般的な流体シミュレーションでは空間をグリッドに分割して流体を表現します.これを「格子法」と呼びます.
一方,流体を粒子で表現しようとするのが「粒子法」です.粒子法はSPH法とMPS法に大別されます.
粒子法にはいろんなメリットがあります(こちらのサイトで詳しく説明されています).
このシリーズでは,MPS法の理論を体系的に解説することを目的とします.ターゲットは「流体力学の数値計算について大まかにご存じで,MPS法に興味を持ってる方」です.
MPS法の基礎理論(一部作成中)
・重み関数と粒子数密度
・勾配モデルと発散モデル
・ラプラシアンモデル
・計算アルゴリズムと圧力のポアソン方程式
・安定性条件
・自由表面境界条件
・壁面境界
・解像度可変型粒子法
高精度化手法(作成中)
高精度微分演算モデル
・CMPS法(運動量・角運動量保存型)
・HL(数学的一貫型)
・GC,LSMPS法(テイラー級数適合型)
・DS法(引張安定型)
高精度ポアソン方程式
・HS
・ECS
高精度境界条件
・SPP(自由表面境界条件)
・WPP(壁面境界条件)
#参考文献
・粒子法(越塚先生)
・粒子法入門
・粒子法(後藤先生)
数式の表記ルール
このシリーズで用いる数式の表記法について記しておきます.各記事では述べないつもりなので,気になったらこちらを参照ください.例としてスカラー $\phi$ の勾配モデルを用います.
math \langle\boldsymbol{\nabla}\phi\rangle_i=\frac{d}{n^0}\sum_{j\ne i}\frac{\phi_{ij}}{|\boldsymbol{r}_{ij}|^2}\boldsymbol{r}_{ij}w_{ij}
| 表記 | 意味 |
|---|---|
| $\langle\alpha\rangle$ | $\alpha$ を離散化した値 |
| $\alpha_i$ | 粒子 $i$ の位置の $\alpha$ |
| $\alpha_{ij}$ | 粒子 $i$ と粒子 $j$ の位置の $\alpha$ の差分 $\alpha_j-\alpha_i$ |
| $\alpha^0$ | $\alpha$ の基準値 |
| $\alpha^k$ | 第 $k$ ステップの $\alpha$ |
| $d$ | 空間の次元数 |
| $n$ | 粒子数密度 |
| $w$ | 重み関数 |
なお,このルールに従うと粒子 $i$ と粒子 $j$ の間の重み関数は $w(|\boldsymbol{r}_{ij}|)$ と表されますが,メンドウなので $w_{ij}$ と表すことにします.すなわち,添え字の $ij$ は「粒子 $i$ と粒子 $j$ の間の」を表すこともあります.