$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$
自作の量子計算シミュレータを使って、一方向量子計算をやってみたよ。
はじめに
量子コンピュータを勉強し始めて最初に触れるのが、基本量子ゲートの組み合わせで状態をユニタリ変換させながら計算する方式なので、これから説明しようとする「一方向量子計算」というのは、ちょっと馴染みがないかと思います(という自分も馴染みがなかったので勉強中です)。まず、その概要説明です(以下の書籍、文献を参考にした、ほぼ受け売り解説になっていますが、汗)。
2001年にラッセンドルフとブリーゲルが、これまでの量子回路計算モデルとはまったく異なる量子計算モデルを提案しました。それは、多数の量子ビットからなる、ある特殊な量子状態(グラフ状態)を用意し、各量子ビットに対して適切に測定を繰り返していくだけで、所望の計算ができるというものです。通常の量子ゲートの操作はユニタリ変換であり逆変換するともとに戻せますが(つまり可逆ですが)、測定という操作はユニタリではない(つまり可逆ではない)ので「一方向量子計算」と言われています。また、測定して観測して、ということを繰り返すので、「測定型量子計算」とか「観測に基づく量子計算」といわれています。
実は、「観測に基づく量子計算」には、もうひとつの方式があります。ベル測定で量子テレポーテーションをさせることを万能計算の基本要素とする「テレポーテーション型量子計算」というものですが、ここでは触れません(未勉強なので)。
さて、従来の量子計算とまったく等価なことができる「測定型量子計算」ですが、従来法と比べて、どんなメリットや意義があるのでしょうか。従来の「量子ゲート方式」は、エンタングルしていない初期量子状態からはじめ、量子ゲートを次々に作用させエンタングルさせながら計算を進めていきますので、計算の途中ずっと量子状態を保っておく必要があります。一方、「測定型量子計算」は、最初に大きくエンタングルした状態を作っておけば、あとは測定という古典的なプロセス(=エンタングルメントの破壊)を繰り返すだけで計算が済みます。この「量子フェーズ」と「古典フェーズ」の分離という際立った特徴が、「物性物理」「量子光学」「誤り耐性量子計算」「暗号」などの研究分野に、ここ十数年の間、新しい視点を提供してくれているとのことです。
理論の確認
一方向量子計算は以下のようなステップでを進めます(参考書籍のp.21-22)。
- N個のキュービットからなる、ある状態を用意する。この状態をリソース状態と呼ぶ。
- 1番目の粒子をある角度で測定し、測定結果を得る。
- その測定結果をもとに、2番目の粒子をどういう角度で測定すべきか古典計算機で計算する。
- 2番目の粒子をその角度で測定し、計算結果を得る。
- その測定結果をもとに、3番目の粒子をどういう角度で測定すべきか古典計算機で計算する。
- 3番目の粒子をその角度で測定し、測定結果を得る。
- 以下これの繰り返し。
- 最後に、決められた個数の粒子をすべて測定し終わったら、測定されずに残った粒子たちの状態が(パウリ演算子を除いて)$U\ket{0}^{\otimes n}$になっている。ここで$U$は実現したいユニタリとする。
最初のリソース状態の決め方として、ラッセンドルフとフリーゲルによって提案されたのが、グラフ状態です。エッジとノードからなるグラフをイメージし、ノードのひとつひとつが粒子に対応するものだと思ってください。そのノードを$\ket{0}$に初期化し、各々にアダマールゲートを作用させて、$\ket{+}$状態にします。そして、接続されているノードの組合せすべてに2量子ゲートである$CZ$
CZ = \ket{0} \bra{0} \otimes I + \ket{1} \bra{1} \otimes Z
を作用させます。そうして、できたものが「グラフ状態」です。このとき、計算したいものに応じて、適切なグラフ構造を用意しておく必要があります。実際の計算は、1粒子ごとにある方向の測定を行いながら進めていきます。どの粒子にどんな方向で測定するかも、計算したいものに応じて適切に設計します。
ちょっと雲をつかむような話になってきているので、2つの粒子からなるグラフ状態を例に、もう少し、具体的に説明します。いま、0番目の粒子(量子ビット)の初期状態を$\ket{\psi}=a\ket{0}+b\ket{1}$とし、1番目の量子ビットの状態を$\ket{+}$にします。この2つの量子ビットに$CZ$ゲートをかけます。これでもっとも簡単なグラフ状態ができあがります。いま0番目の量子ビットが入力状態であると考えているので、0番目は$\ket{+}$にはしません。現在の量子状態を式で書くと、
CZ(\ket{\psi}_{0} \ket{+}_{1}) = a \ket{0}_{0} \ket{+}_{1} + b \ket{1}_{0} \ket{-}_{1}
となります。ここで、0番目の量子ビットを$\ket{0} + e^{i\phi} \ket{1}$基底で測定します(ブロッホ球で言うと、xy平面でZ軸周りに$\phi$回転させた方向)。上向き状態が測定されたとすると、この基底への射影ということになるので、結果の状態は、
\begin{align}
&(\ket{0}_{0} + e^{i\phi} \ket{1}_{0}) (\bra{0}_{0} + e^{i\phi} \bra{1}_{0})
(a \ket{0}_{0} \ket{+}_{1} + b \ket{1}_{0} \ket{-}_{1}) \\
&= (\ket{0}_{0} + e^{i\phi} \ket{1}_{0}) (a \ket{+}_{1} + b e^{i\phi} \ket{-}_{1}) \\
&= (\ket{0}_{0} + e^{i\phi} \ket{1}_{0}) H e^{-i \phi Z_{1}/2} \ket{\psi}_{1}
\end{align}
となります。1番目の量子ビットに注目すると、
H e^{-i \phi Z_{1}/2} \ket{\phi}_{1}
です。つまり、0番目を角度$\phi$で測定することで、最初の状態$\ket{\psi}$をZ軸周りに$-\phi$回転させてアダマールゲートをかけた状態が、1番目の状態に現れるということになります。アダマールとZ回転を組み合わせれば、任意の1量子ビット計算ができるので、この「素過程」を繰り返せば、任意の1量子ビット計算ができるということになります。
いま、測定結果が上向きだったと想定していました。下向きだった場合は、どうなるかと言うと、
X H e^{-i \phi Z_{1}/2} \ket{\psi}_{1}
となり、パウリ演算子が頭についている以外は上向きの結果と同じになります。両方をまとめて書くと、測定による初期状態の変化は、以下のように表すことができます。ここで、0番目の量子ビットの測定結果が上向きだった場合、$s_{0} = 0$で、下向きだった場合、$s_{0} = 1$と定義します。
\ket{\psi}_{0} \rightarrow X^{s_{0}} H Rz(\phi) \ket{\psi}_{1}
さて、それでは、これを次々に実行して、具体的に任意の1量子ビット計算を構成してみます。任意の1量子ビットゲートは3つのオイラー角$(\alpha, \beta, \gamma)$を用いて、$U = Rx(\gamma) Rz(\beta) Rx(\alpha)$と表すことができます。同じことを「一方向量子計算」でやると、どうなるか。答えを先に言います。5つの量子ビットを1次元的に並べたグラフ状態をつくり、以下のような測定を順にしていけば、測定されないで最後に残された量子ビットが、所望の計算結果になっています。
- 0番目の量子ビット(入力状態):X方向の測定を実施
- 1番目の量子ビット:XY平面、Z軸周り角度$\alpha$方向の測定を実施(前段の結果が下向きだった場合、測定角を$-\alpha$とする)
- 2番目の量子ビット:XY平面、Z軸周り角度$\beta$方向の測定を実施(前段の結果が下向きだった場合、測定角を$-\beta$とする)
- 3番目の量子ビット:XY平面、Z軸周り角度$\gamma$方向の測定を実施(0番目と2番目の結果が異なっていた場合、測定角を$-\gamma$とする)
- 4番目の量子ビット:入力状態に対して、$Rx(\gamma) Rz(\beta) Rx(\alpha)$を作用させた状態になっている(ただし、途中の測定結果が何であったかに応じて、いくつかのパウリ演算子が前にかかる)
この操作をイメージしやすいように図で表すと、
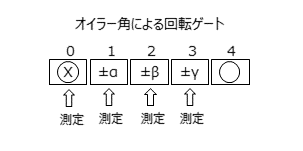
となります。ここで$\alpha,\beta,\gamma$の前についている$\pm$は、前段までの測定結果に応じて回転角の符号を変えるということを意味しています。なぜ、これでいけるのかは、以下のように計算できることからわかります。
\begin{align}
&[X^{s_3} H Rz(\gamma)][X^{s_2} H Rz(\beta)][X^{s_1} H Rz(\alpha)][X^{s_0} H Rz(0)] \ket{\psi} \\
&= [X^{s_3}HRz(\gamma)][X^{s_2} HRz(\beta)] X^{s_1} Z^{s_0} HRz((-1)^{s_0}\alpha) \ket{\psi} \\
&= [X^{s_3} H Rz(\gamma)]X^{s_2+s_0}Z^{s_1}HRz((-1)^{s_1}\beta)Rx((-1)^{s_0}\alpha) \ket{\psi} \\
&= X^{s_3+s_1} Z^{s_2+s_0} Rx((-1)^{s_2+s0}\gamma)Rz((-1)^{s_1}\beta)Rx((-1)^{s_0}\alpha) \ket{\psi}
\end{align}
もう一つ、これよりも簡単な1量子ゲートの例として、アダマールゲートの構成例を示します。先程と同様、5つの量子ビットでグラフ状態をつくります。これに対して、以下の測定を実施します。
- 0番目の量子ビット(入力状態):X方向の測定を実施
- 1番目の量子ビット:Y方向の測定を実施
- 2番目の量子ビット:Y方向の測定を実施
- 3番目の量子ビット:Y方向の測定を実施
- 4番目の量子ビット:入力状態に対して、アダマールゲートを作用させた状態になっている
この場合、測定結果に応じて次段の角度を変えるなどの操作は不要です。これも図で表すと、以下のようになります。
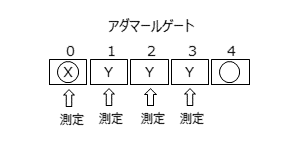
シミュレーション
さて、それでは、以上のことをqlazyで試してみます。
まず、一番簡単な2つの量子ビットを使った素過程です。コードは以下の通りです。入力状態はY軸回転、Z軸回転を使ってランダムにつくっています。また、比較検証のため、従来の量子ゲートでの計算を下の方でやっています。
import random
from qlazypy import QState
def main():
a = random.uniform(0.0, 1.0)
b = random.uniform(0.0, 1.0)
phi = random.uniform(0.0, 1.0)
print("a,b = {0:.4f}, {1:.4f}".format(a,b))
print("phi = {0:.4f}".format(phi))
print("** one-way quantum computing")
# graph state
qs_oneway = QState(2)
qs_oneway.ry(0, phase=a).rz(0, phase=b) # input state (random)
qs_oneway.h(1)
qs_oneway.cz(0,1)
# measurement
s = qs_oneway.m(id=[0], shots=1, angle=0.5, phase=phi)
# result state
qs_oneway.show(id=[1])
print("** conventianal quantum gate")
qs_gate = QState(1)
qs_gate.ry(0, phase=a).rz(0, phase=b) # input state (random)
qs_gate.rz(0, phase=-phi).h(0)
qs_gate.show()
del qs_oneway
del qs_gate
if __name__ == '__main__':
main()
結果は、以下の通りです。0番目の量子ビットの測定結果は上向きだったらしく、従来の量子ゲートの結果とまったく同じ状態になっています。もし測定結果が下向きだった場合は、Xゲートが前にかかるので、c[0]とc[1]は逆転します。
a,b = 0.2124, 0.5799
phi = 0.3458
** one-way quantum computing
c[0] = +0.8541+0.0000*i : 0.7295 |++++++++
c[1] = +0.4598-0.2431*i : 0.2705 |++++
** conventianal quantum gate
c[0] = +0.8541+0.0000*i : 0.7295 |++++++++
c[1] = +0.4598-0.2431*i : 0.2705 |++++
次に、1量子ビットゲートの例として、簡単な方のアダマールゲートをやってみます。コードは以下の通りです。入力状態は$\ket{0}$にしています。
from qlazypy import QState
def main():
print("== hadamard gate ==")
print("** one-way quantum computing")
# graph state
qs_oneway = QState(5)
qs_oneway.h(1).h(2).h(3).h(4)
qs_oneway.cz(0,1).cz(1,2).cz(2,3).cz(3,4)
# measurement
qs_oneway.mx(id=[0], shots=1)
qs_oneway.my(id=[1], shots=1)
qs_oneway.my(id=[2], shots=1)
qs_oneway.my(id=[3], shots=1)
# result state
qs_oneway.show(id=[4])
print("** conventianal quantum gate")
qs_gate = QState(1)
qs_gate.h(0)
qs_gate.show()
del qs_oneway
del qs_gate
if __name__ == '__main__':
main()
結果は、以下の通りです。アダマールゲートが正しくかかっています。
== hadamard gate ==
** one-way quantum computing
c[0] = +0.7071-0.0000*i : 0.5000 |++++++
c[1] = +0.7071-0.0000*i : 0.5000 |++++++
** conventianal quantum gate
c[0] = +0.7071+0.0000*i : 0.5000 |++++++
c[1] = +0.7071+0.0000*i : 0.5000 |++++++
最後に、オイラー角を使った、任意の1量子ビットゲートをやってみます。コードは以下の通りです。こちらも、入力状態は$\ket{0}$にしています。オイラー角はランダムに設定するようにしています。
import random
from qlazypy import QState
def main():
print("== general rotation ==")
alpha = random.uniform(0.0, 1.0)
beta = random.uniform(0.0, 1.0)
gamma = random.uniform(0.0, 1.0)
print("(euler angle = {0:.4f}, {1:.4f}, {2:.4f})".format(alpha, beta, gamma))
print("** one-way quantum computing")
# graph state
qs_oneway = QState(5)
qs_oneway.h(1).h(2).h(3).h(4)
qs_oneway.cz(0,1).cz(1,2).cz(2,3).cz(3,4)
# measurement
alpha_oneway = alpha
beta_oneway = beta
gamma_oneway = gamma
s0 = qs_oneway.m(id=[0], shots=1, angle=0.5, phase=0.0).lst
if s0 == 1:
alpha_oneway = -alpha_oneway
s1 = qs_oneway.m(id=[1], shots=1, angle=0.5, phase=alpha_oneway).lst
if s1 == 1:
beta_oneway = -beta_oneway
s2 = qs_oneway.m(id=[2], shots=1, angle=0.5, phase=beta_oneway).lst
if(s0+s2)%2 == 1:
gamma_oneway = -gamma_oneway
s3 = qs_oneway.m(id=[3], shots=1, angle=0.5, phase=gamma_oneway).lst
# result state
qs_oneway.show(id=[4])
print("** conventianal quantum gate")
qs_gate = QState(1)
qs_gate.rx(0, phase=alpha).rz(0, phase=beta).rx(0, phase=gamma)
qs_gate.show()
del qs_oneway
del qs_gate
if __name__ == '__main__':
main()
結果は、以下の通りです。パウリ行列の分を除き、従来の量子ゲートと同じ状態になり正しく計算されていることがわかります。全体にかかる位相項を除き、さらに正規化をしているので、ちょっとわかりにくいかもしれませんが、確率に相当する値(0.9373と0.0627)を見ていただければ、両者一致していることがわかります。ただし、途中の測定結果によっては、c[0]とc[1]が逆転することはあります。
= general rotation ==
(euler angle = 1.7725, 1.1473, 1.1473)
** one-way quantum computing
c[0] = +0.9681-0.0000*i : 0.9373 |++++++++++
c[1] = -0.1511-0.1997*i : 0.0627 |++
** conventianal quantum gate
c[0] = +0.9681+0.0000*i : 0.9373 |++++++++++
c[1] = +0.1997+0.1511*i : 0.0627 |++
まとめ
測定を繰り返すだけで、こんな計算ができるなんて、ちょっと面白いです。が、理論が難く、ここまで来るのも四苦八苦という感じでした(間違っていることを言っている可能性もあるので、ご指摘いただけるとありがたいです)。いろいろ新しい可能性があるそうなので、引き続き勉強進めます。とりあえず、次は2量子ビット、やってみようと思います。
補足(2021.9.5)
以上