取得データ量を最大化するセンサー設置箇所を求める

やりたいこと

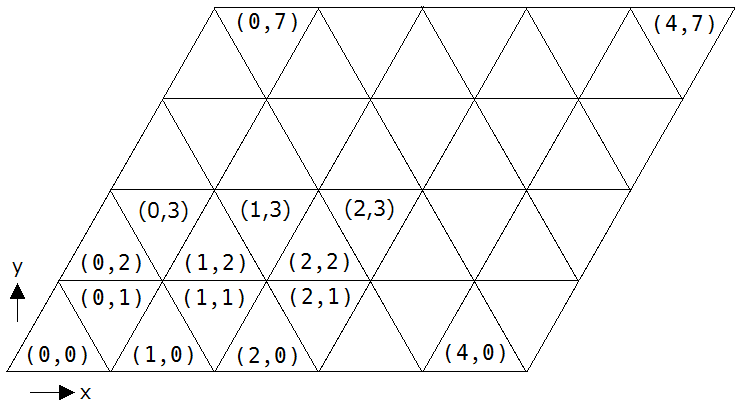
下図のようなエリアがあります。

• この三角形の中央にセンサーを設置して、データ収集をします。
• 総取得データ量を最大化することが目的です。
• 1つの三角形に1つまでしかセンサーは置けません。
• 1つのセンサーを置くと、データ量 3 を取得できます。
• 予め、センサーを設置しなければいけない箇所と、センサーを設置してはいけない箇所が決まっています。
• 下表のように、隣りに別のセンサーがあると、干渉を起こして、取得データ量が各々 1 減ります。(合計 2 減少)
  • 従って、周りに2以上のセンサーがある場合は、設置しない方がよいことになります。

周りのセンサー数	取得データ量	干渉データ量	全体として増えるデータ量
0	3	0	3
1	3	2	1
2	3	4	-1
3	3	6	-3

混合整数最適化問題による最適化(数理問題によるアプローチ)

混合整数最適化問題(Mixed Integer optimization Problem: MIP)としてモデル化してみましょう。
定式化や考え方については、組合せ最適化を使おうを参考にしてください。

定式化

最大化	$取得データ量 \\ = 3 \times 設置するかどうか - 2 \times 干渉するかどうか$
変数	$(センサーを)設置するかどうか \in\{0，1\} \forall 設置箇所$
	$干渉するかどうか \ge 0 \forall 隣接箇所$
制約条件	$設置するかどうか_1 + 設置するかどうか_2 - 干渉するかどうか \le 1$

最小カット問題による最適化(典型問題によるアプローチ)

グラフ理論で最小カット問題というものがあります。

以下のようなs-tグラフを考えます。この有向グラフのs-t最小カットを求めると、元のセンサー設置問題の最適解を得ることができます。
元の問題は最大化問題ですが、"3 － 取得データ量"をコストと考えることにより、最小化問題としてとらえます。
詳しくは、後述の参考サイトをご覧ください。

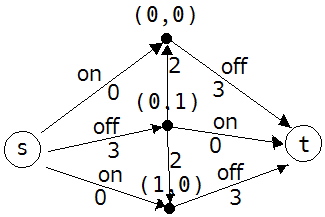
s-tグラフ

• (0,0),(0,1),(1,0)の3つの例を上図に示します。
• 始端ノード"s"から、各箇所(三角形)に辺を引きます。また、各箇所から終端ノード"t"にも辺を引きます。
• 上三角の箇所(上図では(0,0)と(1,0))では、sからの辺は"設置"を表し、tへの辺は"非設置"を表します。
• 下三角の箇所(上図では(0,1))では、sからの辺は"非設置"を表し、tへの辺は"設置"を表します。
• 設置の辺の重みは0とし、非設置の辺の重みは3とします。(重みは、"3 － 取得データ量"です。)
• 全ての隣接箇所に対して、下三角から上三角に、重み2の辺を引きます。
• "設置"で固定する場合、"設置"の辺は削除(カット済み)とし、"非設置"の辺の重みを十分大きくします。
• "非設置"で固定する場合、"非設置"の辺は削除(カット済み)とし、"設置"の辺の重みを十分大きくします。

s-tグラフの意味

• s-tカットするためには、各々の箇所において、設置または非設置の辺のどちらかをカットすることになります。カットされた方を選んだものとみなします。
• s-tカットが成り立つためには、隣接箇所共に設置した場合、干渉の辺もカットする必要があり、干渉量を表現できます。(上三角と下三角で分けたことで上手くいきます。)

最小カット問題について

最小カット問題は、多項式時間で解ける解きやすい問題です。後述のプログラムでは、Pythonのnetworkxを用いて解きます。
ちなみに、最小カット問題の双対問題は、最大流問題です。

pythonによる実行例

準備をします。

python3

import numpy as np, networkx as nx
from pulp import *
def addvar(lowBound=0, var_count=[0], *args, **kwargs):
    """変数作成用ユーティリティ"""
    var_count[0] += 1
    return LpVariable('v%d' % var_count[0], lowBound=lowBound, *args, **kwargs)
def calc(a, r):
    """rを設置箇所として取得データ量を計算"""
    b = a.copy()
    b[b > 1] = 0
    for x, y in r:
        b[y, x] = 1
    s = b.sum() * 3
    for y in range(0, b.shape[0], 2):
        for x in range(b.shape[1]):
            s -= 2 * b[y, x] * b[y+1,x]
            if x:
                s -= 2 * b[y, x] * b[y+1,x-1]
            if y:
                s -= 2 * b[y, x] * b[y-1,x]
    return s

solve_by_mipは、MIPによる解法です。設置箇所を返します。

python3

def solve_by_mip(a):
    """MIPで問題を解き、設置箇所を返す"""
    nm, nn = a.shape
    b = a.astype(object)
    vv1 = [addvar(cat=LpBinary) for _ in range((b > 1).sum())]
    b[b > 1] = vv1
    vv2 = []
    m = LpProblem(sense=LpMaximize)
    for y in range(0, nm, 2):
        for x in range(nn):
            chk(m, vv2, b[y,x] + b[y+1,x])
            if x: chk(m, vv2, b[y,x] + b[y+1,x-1])
            if y: chk(m, vv2, b[y,x] + b[y-1,x])
    m += 3 * lpSum(vv1) - 2 * lpSum(vv2)
    m.solve()
    return [(x, y) for x in range(nn) for y in range(nm)
            if isinstance(b[y,x], LpVariable) and value(b[y, x]) > 0.5]
def chk(m, vv2, e):
    """eが変数を含むならば、共に1であれば目的関数を2減らす制約を追加"""
    if isinstance(e, LpAffineExpression):
        v = addvar()
        vv2.append(v)
        m += e - v <= 1

solve_by_graphは、最小カットによる解法です。同じく設置箇所を返します。

python3

def solve_by_graph(a):
    """最小カット問題で問題を解き、設置箇所を返す"""
    nm, nn = a.shape
    g = nx.DiGraph()
    for y in range(0, nm, 2):
        for x in range(nn):
            if a[y, x] == 0: # off
                g.add_edge('s', (x,y), capacity=7)
            elif a[y, x] == 1: # on
                g.add_edge((x,y), 't', capacity=7)
            else:
                g.add_edge('s', (x,y), capacity=0)
                g.add_edge((x,y), 't', capacity=3)
            if a[y+1, x] == 0: # off
                g.add_edge((x,y+1), 't', capacity=7)
            elif a[y+1, x] == 1: # on
                g.add_edge('s', (x,y+1), capacity=7)
            else:
                g.add_edge('s', (x,y+1), capacity=3)
                g.add_edge((x,y+1), 't', capacity=0)
            g.add_edge((x,y+1), (x,y), capacity=2)
            if x:
                g.add_edge((x-1,y+1), (x,y), capacity=2)
            if y:
                g.add_edge((x,y-1), (x,y), capacity=2)
    r = []
    for s in nx.minimum_cut(g, 's', 't')[1]:
        b = 's' in s
        for t in s:
            if isinstance(t, str): continue
            x, y = t
            if a[y, x] > 1 and b == (y%2 != 0):
                r.append((x, y))
    return sorted(r)

40×80のサイズで、固定箇所をランダムに設置して、結果を比較してみましょう。

python3

nn, nm = 40, 80 # 横、縦
np.random.seed(1)
a = np.random.randint(0, 6, (nm, nn)) # 0; fix off, 1: fix on, ow:select

%time rmip = calc(a, solve_by_mip(a))
%time rgrp = calc(a, solve_by_graph(a))
print(rmip == rgrp)
>>>
Wall time: 455 ms
Wall time: 185 ms

True

• どちらの手法も同じ取得データ量になっている(rmip == rgrp)のが確認できます。
• MIPの方が2倍強、遅いです。
  • 一般に、汎用ソルバーより専用ソルバーの方が計算が速いです。
  • 別途確認したところ、MIPソルバー単体の計算時間は、最小カットによる計算時間を少し上回るくらいでした。
• また、理屈はわかっていないですが、MIPを線形緩和しても取得データ量は変わらず、計算時間は若干早くなります。

参考サイト

• Problem E. The Year of Code Jam: 参考にした問題
• 最小カットを使って「燃やす埋める問題」を解く: 参考にした解法

以上