Blenderでフラクタル

シェルピンスキーのギャスケット

Blenderでシェルピンスキーのギャスケットを作ってみました。

※ 色は別途つけています。

シェルピンスキーのギャスケットの作り方（2次元版）

Scriptingワークスペースで、下記をコピペして実行します。

import bpy
import numpy as np


def sier(pos, size):
    s3 = size * 1.73205
    if size <= 0.2:
        opt = {"radius1": size, "depth": s3, "vertices": 3, "calc_uvs": False}
        bpy.ops.mesh.primitive_cone_add(location=pos + [s3 / 2, size / 2, s3 / 2], **opt)
        bpy.ops.mesh.primitive_cone_add(location=pos + [s3 * 1.5, size / 2, s3 / 2], **opt)
        bpy.ops.mesh.primitive_cone_add(location=pos + [s3, size * 2, s3 / 2], **opt)
        return
    sier(pos, size / 2)
    sier(pos + [s3, 0, 0], size / 2)
    sier(pos + [s3 / 2, size * 1.5, 0], size / 2)

sier(np.zeros(3), 1)

参考：BlenderでPythonを実行する方法

0.2を小さくすると、三角錐が増えていきます。

シェルピンスキーのギャスケットの作り方（3次元版）

シェルピンスキーのギャスケットは2次元でした。Blenderを使っているのですから3次元にしてみましょう。
3個1組を4個1組にすると、下記のようになります。

• Sketchfabで形を確認

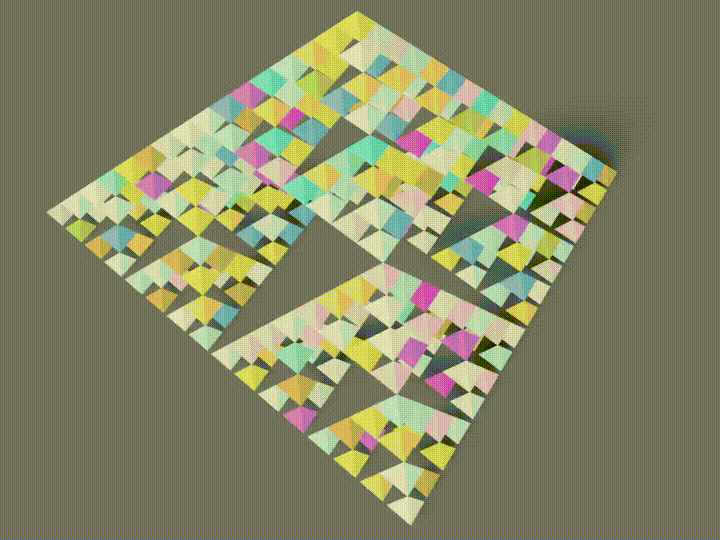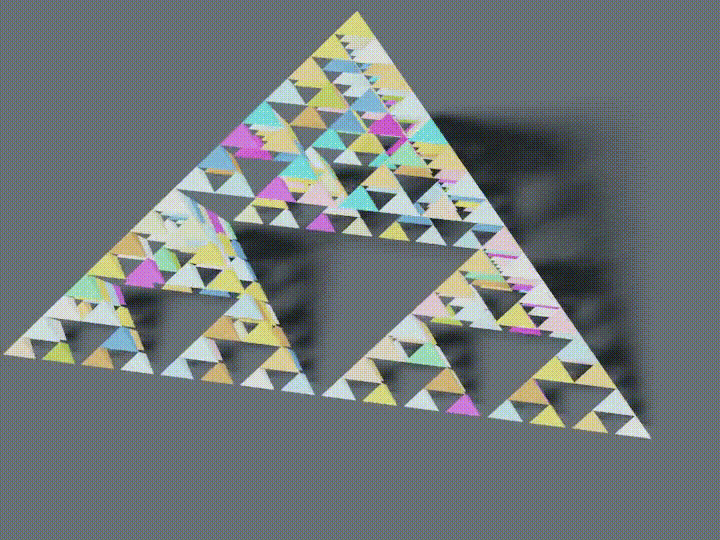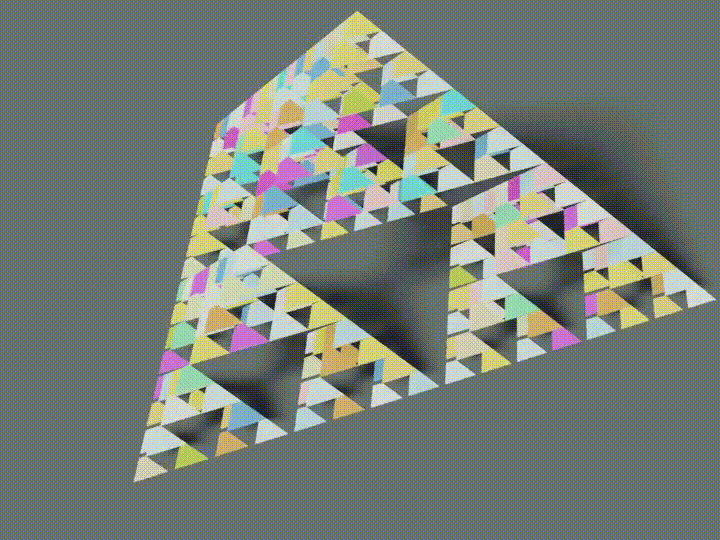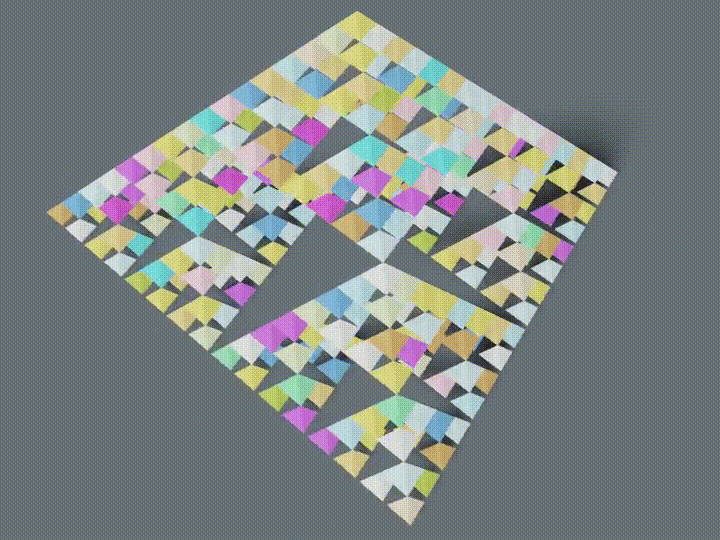
import bpy
import numpy as np


def sier(pos, size):
    s3 = size * 1.73205
    if size <= 0.2:
        opt = {"radius1": size, "depth": s3 / 2, "vertices": 3, "calc_uvs": False}
        bpy.ops.mesh.primitive_cone_add(location=pos + [s3 / 2, size / 2, s3 / 6], **opt)
        bpy.ops.mesh.primitive_cone_add(location=pos + [s3 * 1.5, size / 2, s3 / 6], **opt)
        bpy.ops.mesh.primitive_cone_add(location=pos + [s3, size * 2, s3 / 6], **opt)
        bpy.ops.mesh.primitive_cone_add(location=pos + [s3, size, s3 * 2 / 3], **opt)
        return
    sier(pos, size / 2)
    sier(pos + [s3, 0, 0], size / 2)
    sier(pos + [s3 / 2, size * 1.5, 0], size / 2)
    sier(pos + [s3 / 2, size / 2, s3 / 2], size / 2)

sier(np.zeros(3), 1)

正八面体のフラクタルの作り方

同じようにして正八面体も作れます。

import bpy
import numpy as np
from mathutils import Vector


def add_poly8(pos, s: float):
    pts = [[0, 0, 0], [s, 0, -s], [s, 0, s], [s, -s, 0], [s * 2, 0, 0], [s, s, 0]]
    verts = [Vector(pt + pos) for pt in pts]
    edges = []
    faces = [
        [0, 1, 3], [0, 1, 5], [0, 2, 3], [0, 2, 5],
        [1, 3, 4], [1, 4, 5], [2, 3, 4], [2, 4, 5]
    ]
    mesh = bpy.data.meshes.new(name="Poly8")
    mesh.from_pydata(verts, edges, faces)
    obj = bpy.data.objects.new(mesh.name, mesh)
    bpy.context.scene.collection.objects.link(obj)


def frac(pos, size):
    if size <= 0.2:
        add_poly8(pos, size)
        add_poly8(pos + [size * 2, 0, 0], size)
        add_poly8(pos + [size, size, 0], size)
        add_poly8(pos + [size, -size, 0], size)
        add_poly8(pos + [size, 0, size], size)
        add_poly8(pos + [size, 0, -size], size)
        return
    frac(pos, size / 2)
    frac(pos + [size * 2, 0, 0], size / 2)
    frac(pos + [size, size, 0], size / 2)
    frac(pos + [size, -size, 0], size / 2)
    frac(pos + [size, 0, size], size / 2)
    frac(pos + [size, 0, -size], size / 2)


frac(np.zeros(3), 1)

シェルピンスキーダイヤモンドの作り方

正八面体のフラクタルだと詰まりすぎてる感じがしたので、シェルピンスキーのギャスケットを四角錐にしてz軸方向にも追加したものも作ってみました。

import bpy
import numpy as np
from mathutils import Vector


def add_tri(pos, s: float, z):
    pts = [[0, 0, 0], [s, 0, s * z], [s, -s, 0], [s * 2, 0, 0], [s, s, 0]]
    verts = [Vector(pt + pos) for pt in pts]
    edges = []
    faces = [[0, 1, 2], [0, 1, 4], [1, 2, 3], [1, 3, 4], [0, 2, 3, 4]]
    mesh = bpy.data.meshes.new(name="Tri")
    mesh.from_pydata(verts, edges, faces)
    obj = bpy.data.objects.new(mesh.name, mesh)
    bpy.context.scene.collection.objects.link(obj)


def frac(pos, size, z):
    if size <= 0.2:
        add_tri(pos, size, z)
        add_tri(pos + [size * 2, 0, 0], size, z)
        add_tri(pos + [size, size, 0], size, z)
        add_tri(pos + [size, -size, 0], size, z)
        add_tri(pos + [size, 0, size * z], size, z)
        return
    frac(pos, size / 2, z)
    frac(pos + [size * 2, 0, 0], size / 2, z)
    frac(pos + [size, size, 0], size / 2, z)
    frac(pos + [size, -size, 0], size / 2, z)
    frac(pos + [size, 0, size * z], size / 2, z)


frac(np.zeros(3), 1, 1)
frac(np.zeros(3), 1, -1)

• Sketchfabで形を確認

以上