組合せ最適化で消防署の位置を決めよう

問題

あなたは、新しくできた A市の市長です。新たに消防署を3つ建てることにしました。
さて、どこに建てたらよいでしょうか？
(この話はフィクションです)

考え方その1

容量制約なし施設配置問題として考えます。
市民の世帯の位置はわかっているものとします。各世帯から最寄の消防署の位置への距離の総和が最小になるように決めてみましょう。

Pythonで解く

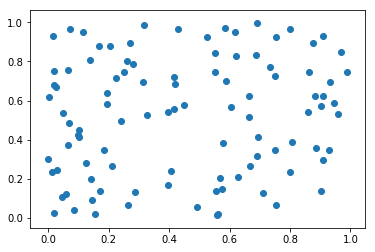
まず、世帯位置をランダムに決めます。

python

%matplotlib inline
import numpy as np, pandas as pd, matplotlib.pyplot as plt
from ortoolpy import facility_location_without_capacity
np.random.seed(1)

世帯数,消防署数 = 100,3
世帯位置 = np.random.rand(世帯数,2)
plt.scatter(*世帯位置.T);

解いてみます。

python

結果1 = facility_location_without_capacity(消防署数,世帯位置)
np.unique(結果1)
>>>
array([ 9, 62, 77])

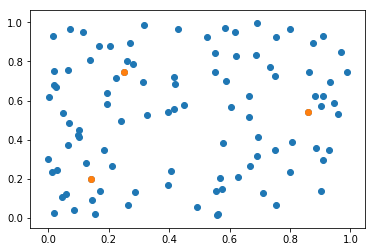
世帯位置の9番目、62番目、77番目に建てるとよいことがわかりました。
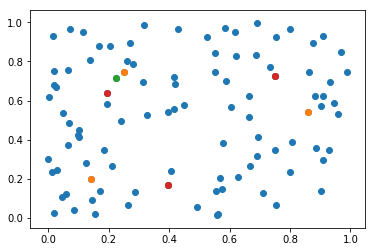
可視化します。

python

消防署位置1 = 世帯位置[np.unique(結果1)]
plt.scatter(*世帯位置.T)
plt.scatter(*消防署位置1.T);

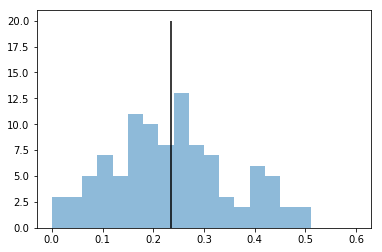
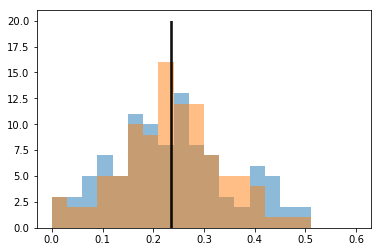
世帯ごとの距離の分布を見てみましょう。中央の線は平均です。

python

距離1 = np.linalg.norm(世帯位置 - 世帯位置[結果1], axis=1)
plt.hist(距離1, range=(0,0.6), bins=20, alpha=0.5)
plt.vlines(距離1.mean(), 0, 20);

考え方その2

距離の総和だと、遠い人と近い人が相殺されてしまいます。なるべく遠くの人が少なくなるようにしましょう。ここでは、距離の2乗の和を最小化させます。

python

結果2 = facility_location_without_capacity(消防署数,世帯位置,
    func = lambda i,j: (世帯位置[i][0]-世帯位置[j][0])**2+(世帯位置[i][1]-世帯位置[j][1])**2)
np.unique(結果2)
>>>
array([37, 39, 73])

違う場所になりました。
PuLPで数理モデルを作ると、下記のようになります。(同じ結果になります)

python

from pulp import *
from ortoolpy import addbinvars, addvars
r = range(len(世帯位置))
m = LpProblem()
x = addvars(len(世帯位置), len(世帯位置))
y = addbinvars(len(世帯位置))
m += lpSum(((世帯位置[i][0]-世帯位置[j][0])**2+(世帯位置[i][1]-世帯位置[j][1])**2) * x[i][j]
           for i in r for j in r)
m += lpSum(y) <= 消防署数
for i in r:
    m += lpSum(x[i]) == 1
    for j in r:
        m += x[i][j] <= y[j]
m.solve()
結果2 = [int(value(lpDot(r, x[i]))) for i in r]

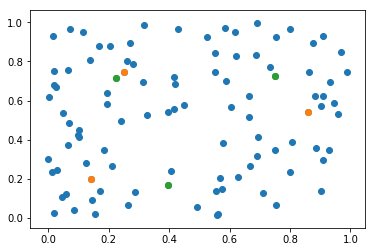
可視化します。

python

消防署位置2 = 世帯位置[np.unique(結果2)]
plt.scatter(*世帯位置.T)
plt.scatter(*消防署位置1.T)
plt.scatter(*消防署位置2.T);

中心寄りに近づいた感じがします。分布を比較して見ましょう。

python

距離2 = np.linalg.norm(世帯位置 - 世帯位置[結果2], axis=1)
plt.hist(距離1, range=(0,0.6), bins=20, alpha=0.5)
plt.vlines(距離1.mean(), 0, 20)
plt.hist(距離2, range=(0,0.6), bins=20, alpha=0.5)
plt.vlines(距離2.mean(), 0, 20)
print('平均', 距離1.mean(), 距離2.mean())
print('分散', 距離1.var(), 距離2.var())
>>>
平均 0.235140814776 0.237069972634
分散 0.0138310436529 0.0100843497562

平均は、わずかに増えましたが、ばらつきが減り、距離の遠い人が減っているのが確認できます。

考え方その3

1番目に近いところから行ける可能性は 90%、2番目に近いところから行ける可能性は 10%として、期待値が最小になるようにしましょう。
1番目用、2番目用の変数を用意して、1番目と2番目を同時に選ばないようにすればOKです。

python

m = LpProblem()
x1 = np.array(addvars(len(世帯位置), len(世帯位置))) # 1番目に近い消防署
x2 = np.array(addvars(len(世帯位置), len(世帯位置))) # 2番目に近い消防署
y  = addbinvars(len(世帯位置))
m += lpSum(((世帯位置[i][0]-世帯位置[j][0])**2+(世帯位置[i][1]-世帯位置[j][1])**2) * x1[i,j] * 0.9
          +((世帯位置[i][0]-世帯位置[j][0])**2+(世帯位置[i][1]-世帯位置[j][1])**2) * x2[i,j] * 0.1
           for i in r for j in r)
m += lpSum(y) <= 消防署数
for i in r:
    m += lpSum(x1[i]) == 1
    m += lpSum(x2[i]) == 1
    for j in r:
        m += x1[i,j] + x2[i,j] <= y[j]
m.solve()
結果3 = [int(value(lpDot(r, x1[i]))) for i in r]
np.unique(結果3)
>>>
array([37, 39, 93])

可視化してみます。ちょっとだけ変わりました。

python

消防署位置3 = 世帯位置[np.unique(結果3)]
for i in [世帯位置,消防署位置1,消防署位置2,消防署位置3]:
    plt.scatter(*i.T)

以上