これなに
「テーブルモデリング言語」というのを思いついたので、紹介します。
何に使うの?
組合せ最適化における数理モデルを図表で表現するのに使います。
数独の例
(ステップ0) 問題をまとめる
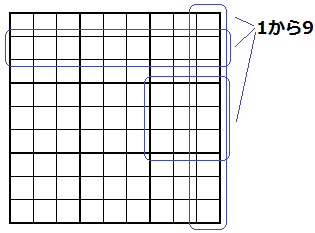
9x9のマスに「1から9の数字」を入れて、行、列、3x3 ごとに同じ数字が表われないようにする。
予め指定されている数字は、それを用いる。
(ステップ1) 変数を決める
数独では、9×9のマスに1から9の数字を求めますので、それを変数にすればよいのですが、テクニック その1を用いて、$i$行$j$列が数字$k+1$かどうかを $x_{ijk} \in \{0,1\}$ で表現します。
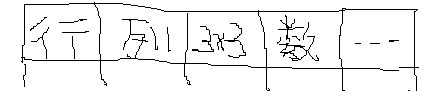
(ステップ2) 1変数1行となる表を作成する
1行が1変数に対応する表を手書きします。そこに、属性として必要なものを記入していきます。
(ステップ4) 必要なマークを記入する
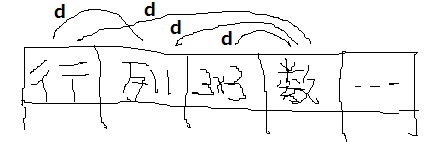
列の右肩に下記のようなマークを入れていきます。
- o:その列を目的関数の係数とします。
- f:その列の非数値(NaN)以外の値で変数を固定します。
- d:その列または列の組でグルーピングしたグループごとに、変数の和が1になるようにします。
(ステップ5) 目的関数、制約条件を適宜追加する
必要に応じて、目的関数、制約条件を追加します。できれば、図でかけるとよいです。
(参考書籍:頭がよくなる「図解思考」の技術)
(ステップ6) 数理モデルとして実装する
- 表をpandasのDataFrameとして作成します。
- 変数として「Var」の列を追加します。
- マーク o の場合、目的関数として、「m += lpDot(a.該当列, a.Var)」を設定します。
- マーク f の場合、制約条件として、該当列がTrueの各行ごとに「m += r.Var == 1」を追加します。
- マーク d の場合、制約条件として、groupby して「m += lpSum(v.Var) == 1」を追加します。
- 求解後、結果として「Val」の列を追加します。
ただし、mは数理モデル(LpProblem)、aは表(DataFrame)、rは行(a.iterrowsのSeries)、vは部分表(groupbyの2つ目)を表すものとします。
Pythonで実行
「Pythonで数独」の例を解いてみましょう。
表を作ります。
import re, pandas as pd
from pulp import *
from itertools import product
from ortoolpy import addbinvars
data = """\
4 . . |. . . |1 . .
. 5 . |. 3 . |. . 8
2 . . |7 . 8 |. 9 .
------+------+------
. 4 5 |6 . . |8 . 1
. . 3 |. 5 . |. . .
. 2 . |1 . 3 |. . .
------+------+------
8 . . |. . 5 |. . .
. . 4 |. . . |. . .
. 1 . |. 6 4 |3 . 9
"""
r = range(9)
s = re.sub(r'[^\d.]','',data)
a = pd.DataFrame([(i,j,(i//3)*3+j//3,k+1,c==str(k+1))
for (i,j),c in zip(product(r,r),s) for k in r],
columns=['行','列','_3x3','数','固'])
a['Var'] = addbinvars(len(a))
a[:1]
| 行 | 列 | _3x3 | 数 | 固 | Var | |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | False | v0001 |
数理モデルを作成し、求解します。
m = LpProblem()
for cl in [('行','列'),('行','数'),('列','数'),('_3x3','数')]:
for _,v in a.groupby(cl):
m += lpSum(v.Var) == 1
for _,r in a[a.固==True].iterrows():
m += r.Var == 1
m.solve()
a['Val'] = a.Var.apply(value)
a[a.Val==1].数.values.reshape(9,9).tolist()
>>>
[[4, 7, 8, 5, 9, 6, 1, 2, 3],
[6, 5, 9, 2, 3, 1, 7, 4, 8],
[2, 3, 1, 7, 4, 8, 6, 9, 5],
[9, 4, 5, 6, 7, 2, 8, 3, 1],
[1, 8, 3, 4, 5, 9, 2, 6, 7],
[7, 2, 6, 1, 8, 3, 9, 5, 4],
[8, 9, 7, 3, 2, 5, 4, 1, 6],
[3, 6, 4, 9, 1, 7, 5, 8, 2],
[5, 1, 2, 8, 6, 4, 3, 7, 9]]
簡単な図でモデルを表現し、機械的にプログラム化して解けることが確認できました。
テクニック(参考)
(その1)特定の数字に着目する場合、0-1変数を使う
例えば、数独で $i$行$j$列の数字を表現する場合、$x_{ij} \in \{1,2,\cdots,9\}$ が$k$かどうかを見るのではなく、$x_{ijk} \in \{0,1\}$ を用いる。
以上