最適化にまつわる話
- ミニサム問題とは、合計(サム:sum)を最小化(ミニ:min)する問題。
- ミニマックス問題とは、最大値(マックス:max)を最小化(ミニ:min)する問題。
避難計画問題に当てはめると、次のようになります。
- ミニサム問題: 全員の避難時間の合計の最小化。
- ミニマックス問題: 最も逃げ遅れる人の避難時間の最小化。
一般に数理最適化ソルバーでは、次のことが言えます。
- ミニマックス問題よりミニサム問題の方が解きやすい。
確かめてみましょう。
python
import numpy as np, pandas as pd, matplotlib.pyplot as plt
from pulp import *
商品数 = 1000
ユーザ数 = 100
np.random.seed(1)
a = pd.DataFrame(np.random.rand(商品数, ユーザ数),
index=['商品%d'%i for i in range(商品数)],
columns=['ユーザ%d'%j for j in range(ユーザ数)])
a['Var'] = [LpVariable('v%d'%i, lowBound=0) for i in range(商品数)]
| ユーザ0 | ユーザ1 | ユーザ2 | ユーザ3 | ユーザ4 | ... | ユーザ99 | |
|---|---|---|---|---|---|---|---|
| 商品0 | 0.417022 | 0.720324 | 0.000114 | 0.302333 | 0.146756 | ... | 0.186260 |
| ... | ... | ... | ... | ... | ... | ... | ... |
| 商品999 | 0.950176 | 0.556653 | 0.915606 | 0.641566 | 0.390008 | 0.485991 | 0.604310 |
1000個の商品に対して。100人のユーザがバラバラの費用感を持っているとします。
下記の問題に対して、1000個の商品の中から、半分を選ぶとします。
- ミニサム問題: 全ユーザの費用感の合計の最小化
- ミニマックス問題: 各ユーザの費用感の最大値の最小化
商品の数を変えながら、計算時間を見てみましょう。
python
it = [100, 200, 500, 1000] # 商品数リスト
tm = []
for n in it:
b = a[:n]
# ミニサム問題
m1 = LpProblem() # 最小化問題(ミニ)
m1 += lpDot(b.T[:-1].sum(), b.Var) # 合計(サム)
m1 += lpSum(b.Var) <= int(n * 0.5)
m1.solve()
# ミニマックス問題
m2 = LpProblem() # 最小化問題(ミニ)
y = LpVariable('y', lowBound=0)
# y >= max(ユーザj の価値)
for j in range(ユーザ数): m2 += y >= lpDot(b.ix[:, j], b.Var)
m2 += y # 合計(マックス)
m2 += lpSum(b.Var) <= int(n * 0.5)
m2.solve()
tm.append((m1.solutionTime, m2.solutionTime))
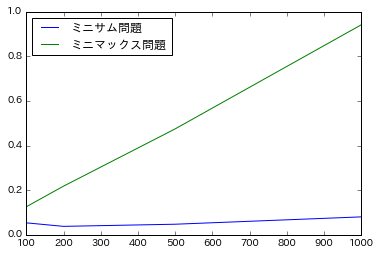
plt.plot(it, tm)
plt.legend(['ミニサム問題','ミニマックス問題'], loc='upper left')
plt.show()
ミニサム問題に比べて、ミニマックス問題の方が、かなり時間がかかります。
ミニマックス問題が時間がかかるのは、何故?
- ミニサム問題に比べて、ミニマックス問題は、最適解がたくさんあります。
- ソルバーでは、全ての可能性を探索しています。
- 最適解がたくさんあると、ソルバーが効率よく計算できません。
ミニマックス問題を効率よく解けないの?
場合によっては、ビンパッキング問題の解き方のように、2段階に解いた方が早く解けることもあります。
以上