こんにちは!
東京テクニカルカレッジ(TTC)アドベントカレンダー2022 14日目です。
2022年はご縁がありTTCさんにて非常勤講師をさせていただきました。
そのつながりで、こちらのアドベントカレンダーにも参加させていただこうと思います!
東京テクニカルカレッジについて
専門学校東京テクニカルカレッジ は、「高い技術力と豊かな人間性を備えたプロフェッショナルを育成し、職業教育を実践する専門学校」として教育を実践する専門学校で、その理念に則りさまざまなカリキュラムが開講されています。
私は、その中で「データサイエンス・AI科」にて非常勤講師を担当させていただきました。
もし、「データサイエンスについて学びたい」と考えている方はぜひ調べてみてください!
この記事で書くこと
この記事では、時系列分析について書きます。
具体的には、「相互相関」というものについてです。
pythonの各ライブラリでの実装を解説したものが少なく苦労したことがあるので、備忘録がてら、こちらに自分の理解をまとめようと思います。
この記事のタイトルから見てくれる人は「時系列分析」についてはご存知かと思いますが、学生さんが読んでくれるかもしれないので、時系列分析についての基本的なところにも軽く触れていこうと思います。
(ご存知の方は読み飛ばしてください)
時系列データとは
時系列データとは、以下のような特徴を持ったデータのことを言います。
- 時間と共に変動し観測されるデータのこと
- 観測される順番に意味があることが特徴
- 同一のものに関する時系列データであったとしても、そこから差分をとったり変化率を考えることで、全く異なる時系列データを生成できる
- 例えば観測値と、そこから得られる変化率の時系列データは全く異なる時系列データである
株価のデータとかはこの典型例ですね。
また、私は普段株式会社セラクのみどりクラウド事業部という部署でデータ分析を行っています。
弊社の製品みどりクラウドでは、センサーを使った農場の環境データを取得していて、このようなセンサーを用いて一定間隔で取得されているデータも時系列データです。
時系列分析の目的
時系列データを分析するモチベーションとしては、以下のようになるかと思います。
- 時系列データが持っている多様な特徴を記述できるモデルを構築すること
- さらに、モデルを用いて、目的(ビジネス的な)に応じた分析を行うこと
このような目的を達成するためには、過去のデータであったり、同時に計測された時系列データとの関係性を分析する必要があるわけなんですね。
相互相関をみる
いきなり「相互相関」まで飛躍しましたが、本記事の趣旨ですのでご容赦ください。
ここでは、同時に観測された$m$種類の時系列データがある場合を考えます。(つまり、$m$系列の多変量時系列データを考えます)
相互相関とは、このような時系列データについて、$i$番目の時系列$y_{n}(i)$と、そこから$k$だけ時間が離れた$j$番目の時系列$y_{n-k}(j)$との間の相関係数のことを言い、以下のように書きます。
$$R_{k}(i, j) = Cor(y_{n}(i), y_{n-k}(j))$$
これをラグ$k$についての関数としてみたものを相互相関関数といいます。
(信号処理のものとは微妙に定義が異なります)

この相関係数を求めるにはどうしたら良いでしょうか。
インターネットで検索して見ると、Pythonでは、以下のやり方があると出てきます。
numpy.correlatescipy.signal.correlatematplotlib.pyplot.xcorr
少し計算してみましょう
import numpy as np
from scipy.signal import correlate
a = np.array([1, 2, 3, 4, 5])
b = np.array([1.5, 2, 2.5, -1, -2])
# 相互相関
xc_np = np.correlate(a, b)
xc_sp = correlate(a, b)
print(xc_np)
print(xc_sp)
# 出力結果
xc_np : array([-1.])
xc_sp : array([-2. , -5. , -5.5, -4. , -1. , 14. , 25. , 16. , 7.5])
二つで異なる結果が得られてしまった上に、「相関係数」とイメージしていた[ -1, 1 ]の範囲からは外れた数値が算出されてしまいました。
いったいどういうことでしょうか。
まず、出力結果が異なる理由ですが、これはnumpyの方の引数を指定してあげると一致します。
# 出力結果をnumpyとscipyで一致させる
xc_np = np.correlate(a, b, mode='full')
print(xc_np)
# 出力結果
xc_np : array([-2. , -5. , -5.5, -4. , -1. , 14. , 25. , 16. , 7.5])
では、この計算はどこからきたのでしょうか。
これは、相関係数の定義を考えてあげると解決します。
長さが同じ二つのデータ、$x$, $y$を考えます。
各々は1次元配列で、$\boldsymbol{x}$, $\boldsymbol{y}$ とベクトルで表すことにしましょう。
このとき、この2データの相関係数は、定義式から以下のように書くことができます。
$Corr = \frac{s_{xy}}{s_{x}s_{y}}$
すなわち、
$Corr = \frac{\frac{1}{n}\Sigma{(x_{i}-\bar{x})(y_{i}-\bar{y})}}{\sqrt{\frac{1}{n}\Sigma{(x_{i}-\bar{x})}^{2}}\sqrt{\frac{1}{n}\Sigma{(y_{i}-\bar{y})}^{2}}}$
この式は、分母分子を$\frac{1}{n}$で約分することができるので、
$Corr = \frac{\Sigma{(x_{i}-\bar{x})(y_{i}-\bar{y})}}{\sqrt{\Sigma{(x_{i}-\bar{x})}^{2}}\sqrt{\Sigma{(y_{i}-\bar{y})}^{2}}}$
ここで、$\boldsymbol{x}$、$\boldsymbol{y}$ をそれぞれ$\bar{x}$, $\bar{y}$ だけ平行移動させたベクトル $\boldsymbol{u}$, $\boldsymbol{v}$ を考えます。(つまり、偏差ベクトルを考えます)
相関係数式は、分子が $\boldsymbol{u}$, $\boldsymbol{v}$の内積、分母が $\boldsymbol{u}$, $\boldsymbol{v}$ の大きさ(L2ノルム)になっていることがわかります。すなわち、
$Corr = \frac{\boldsymbol{u}・ \boldsymbol{v}}{|\boldsymbol{u}||\boldsymbol{v}|}$
内積の定義式より、 $\boldsymbol{u}$ と $\boldsymbol{v}$ の成す角を $\theta$とすれば、
$\boldsymbol{u}・ \boldsymbol{v} = |\boldsymbol{u}||\boldsymbol{v}|cos\theta$ だから、
相関係数は、$cos\theta$となります。
このことから、二つのデータ$x$, $y$の相関係数を考えるためには、$\boldsymbol{u}$, $\boldsymbol{v}$の内積と大きさ(L2ノルム)が計算できればよい、ということになります。
相互相関関数は、一方をちょっとずつずらしながら相関係数を計算していきそれを並べたものをラグ$k$の関数として定義したものなので、「片方をちょっとずつずらしながら内積を計算する」ことで計算できます。
さて、長くなりましたが、数値計算上はこのことを利用しているわけです。
実際、例に挙げた二つのデータ$a$, $b$について、内積を計算してやると
np.dot(a, b)
# -1.0
となり、「最初に計算したnumpy.correlateの実行結果」および、「scipy.signal.correlate の出力中央の値」と一致します。
計算結果が内積であること、相互相関関数を計算するためには片方を少しずつずらしながら内積を計算すればいいということから、出力結果の謎も解けます。
ずらしながら、重なった部分で内積を計算しているわけですね。
では、matplotlibの実装も見てみます。
ドキュメントによると、numpy.correlateで、mode=fullとしているそうなので、計算結果は一致しそうです。
from matplotlib.pyplot import xcorr
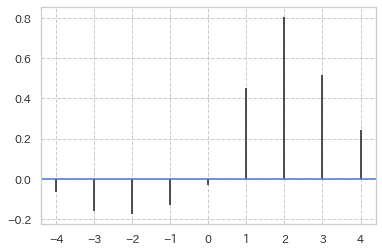
lags, xc_mp, fig, ax = xcorr(a, b, maxlags=4)
# 出力
lags : array([-4, -3, -2, -1, 0, 1, 2, 3, 4])
xc_mp : array([-0.06446584, -0.16116459, -0.17728105, -0.12893167, -0.03223292, 0.45126086, 0.80582296, 0.5157267 , 0.24174689])
・・・と、またしても一致しませんでした。
こんな風に、何も考えず3種類の方法で「相互相関」なるものを考えようとすると、全部違う結果が出てくるんですね。
しかし、このmatplotlibの実装が一番相関係数っぽそうです。
これは何をしているのかというと、xcorrの引数normedが関係していて、デフォルトではTrueになっています。
この処理は、「内積を入力データのL2ノルムの積で割って正規化する」という処理です。
以下の処理が一致します。
xc_np = np.correlate(a, b, mode='full')
xc_np /= (np.linalg.norm(a, ord=2) * np.linalg.norm(b, ord=2))
# 出力
xc_np : array([-0.06446584, -0.16116459, -0.17728105, -0.12893167, -0.03223292, 0.45126086, 0.80582296, 0.5157267 , 0.24174689])
これでようやく3つの実装の違いがわかりました。
めでたしめでたし・・・?
相互相関を計算する
ここまでやってお気づきでしょうか。
そう、いずれの実装も 「入力された配列について、ずらしながら内積を計算する」 ものなのです。
この内積の計算は、信号処理において「類似波形を検知する」ためには十分なのですが、私たちは相関まで知らなければなりません。
つまり、numpy.correlateや、scipy.signal.correlateに入力する配列は元のベクトルではなく、偏差ベクトルでないといけません。
やりたかった計算は以下のようになります。
# 例: numpyでの実装
# 偏差ベクトルを求める
a_dev = a - a.mean()
b_dev = b - b.mean()
# 内積の計算
xc_ab = np.correlate(a_dev, b_dev, mode='full')
# 相関係数にするために正規化をする
xc_ab /= (np.linalg.norm(a_dev, ord=2) * np.linalg.norm(b_dev, ord=2))
# 出力
xc_ab : array([ 0.41500518, 0.46289039, -0.17557911, -0.58260343, -0.79808688, -0.17557911, 0.41500518, 0.29529215, 0.14365564])
このとき、入力配列をどちらも同じものにすれば、自己相関になるはずです。
# 自己相関の計算
acorr_a = np.correlate(a_dev, b_dev, mode='full')
acorr_a /= (np.linalg.norm(a_dev, ord=2) * np.linalg.norm(a_dev, ord=2))
# 出力
acorr_a : array([-0.4, -0.4, -0.1, 0.4, 1. , 0.4, -0.1, -0.4, -0.4])
同じ配列をずらしながら計算しているので、左右対称の配列です。
いわゆる自己相関は、後半5要素。
続いて、statsmodelsの計算結果と一致するか確かめておきましょう。
# 自己相関を計算して一致するか確かめる
from statsmodels.tsa.stattools import acf
acorr = acf(a, nlags=4)
# 出力
acorr : array([ 1. , 0.4, -0.1, -0.4, -0.4])
無事一致しました。
まとめ
相互相関を、Pythonの3種類のライブラリを用いて計算、比較してみました。
データサイエンスの領域は日々民主化が進んでいて、計算式やプログラムの中身なんて知らなくてもある程度のことができるようになってきています。
一方で、今回の例のように、計算式を知らないと見当違いのことをしてしまうことも多々あります。
安易に便利な実装を活用する前に、一歩理解を進めてみることが身を助けるかもしれません。(自戒を込めて)
参考文献
numpy.correlate
scipy.signal.correlate
matplotlib.pyplot.xcorr