研究でたまたま遺伝的アルゴリズムで解く研究をしていたことと,
将来に向かって手数を増やすという意味で作ってみました.
巡回セールスマン問題とは?
$n$ 箇所ある地点に一筆書きをしたらどのような順番で最も短く通ることができるかを考える問題です.
一筆書きする都市の数が$n$ 箇所ある場合,考えられる組み合わせの数は$\frac{(n-1)!}{2}$ 通りあります.
遺伝的アルゴリズムとは?
生物の進化をモデリングした進化計算の一つです.
解の組み合わせを染色体に見立て,交叉・突然変異といった遺伝子操作を繰り返しながら解を進化させて,最終的に最も優れた解を求めていきます.
クラスの流れ
Javaでプログラミングするので,クラスごとに順にみていきます.
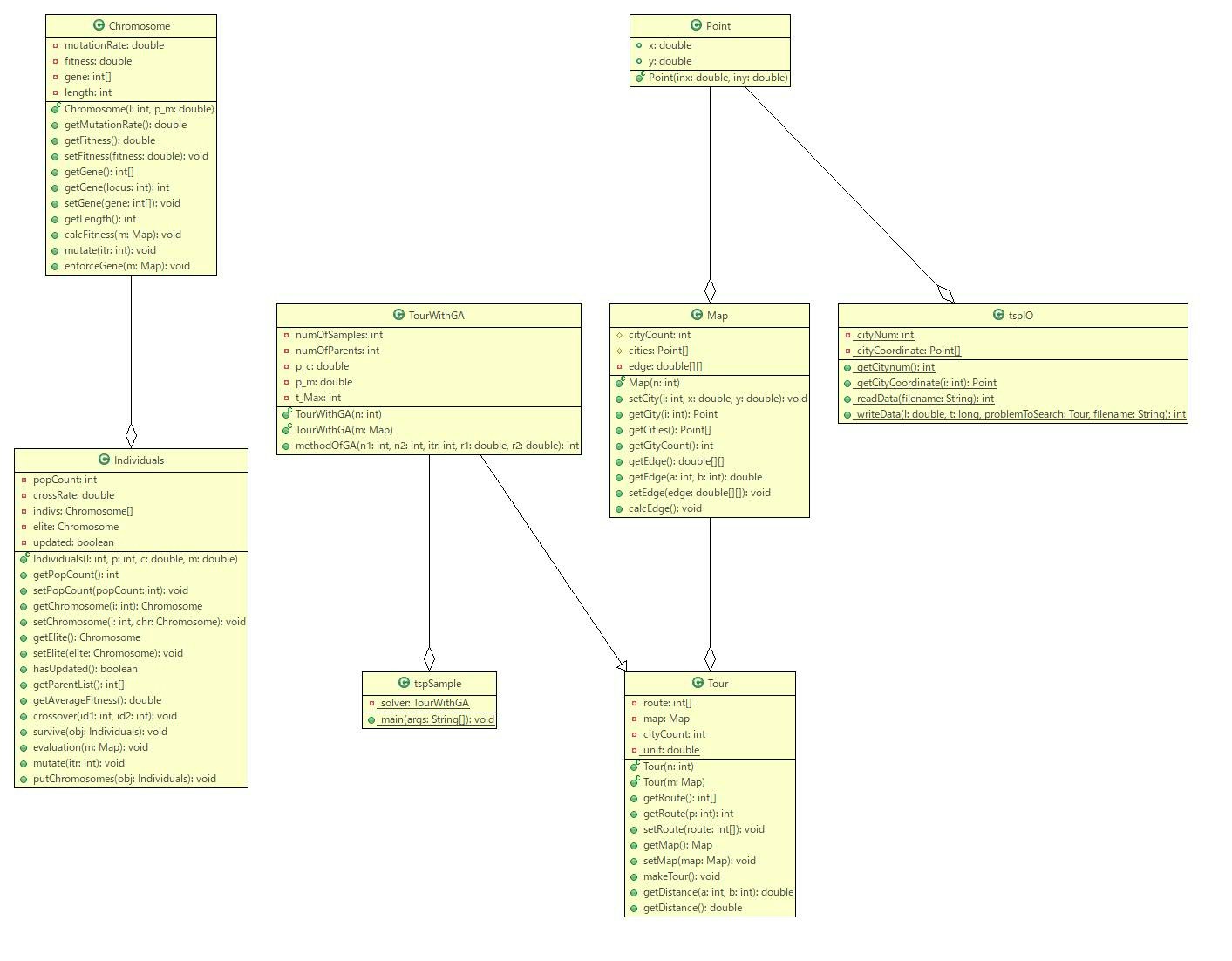
クラス図は下の通りです.
設計で参考にした文献はこちら1
- Pointクラス:$x$, $y$ 各座標を格納します.
- Mapクラス: Pointクラスのデータを集約して,地図としてまとめるクラスです.
- Tourクラス: Mapクラスをもとに経路を記憶するクラスです.
- TourWithGAクラス:Tourクラスから派生して,遺伝的アルゴリズムを解かせるクラスです.
- tspSampleクラス: メインとなるクラスです.
- tspIOクラス: ファイルから座標を読み込むクラスです.
- Sortクラス: 個体の順位付けを行うためのクラスです.(上のクラス図には入っていません.)
- Chromosomeクラス: 染色体のクラスです.遺伝子が配列となって入っています.
- Individualsクラス: 個体群のクラスです.Chromosomeクラスの集合と,Chromosome型のエリート染色体が記憶されています.
その中で遺伝的アルゴリズムは,TourWithGA, Chromosome, Individualsの3つを使います.
遺伝子操作については,Chromosomeクラスでは,突然変異と遺伝子の適合度計算を行うメソッドが,Individualクラスでは,交叉と遺伝子の再生・選択,エリートの保存がメソッドとして実装されています.
戦略としては,前川ら2 が提案した枝交換交叉(EXX)の手法を参考に作成しています.
遺伝的アルゴリズムの動作
ソースコードが多いので,詳しいところはソースコードを見てください.
遺伝的アルゴリズムにおける動作に絞って,仕様を説明していこうと思います.
地図データ
巡回セールスマン問題における都市の位置はCSVファイルで入力していきます.
CSVファイルの中身としては,
52,
565,575
25,185
345,750
945,685
845,655
880,660
25,230
・
・
・
最初の行では,読み込むことができる都市の数を入力します.
2行目以降から,都市の$x$ 座標と$y$ 座標を入力します.
プログラムのメインクラスはtspSampleです.javaで実行するときに,
$ java tspSample <読み込むCSVファイル>
といった具合に実行してください.
読み込みに成功すれば,
city_num= 52
565.000 575.000
25.0000 185.000
345.000 750.000
945.000 685.000
845.000 655.000
・
・
・
このように,読み込んだ都市数と都市データがコンソールに出力されます.
初期個体生成
Individuals型のchildrenに遺伝子操作を行う初期個体群を生成します.
具体的には,Chromosomeクラスには遺伝子配列として都市の順列として表現しています.
Tourクラスには,makeTour()という,ランダムに巡回路を生成するメソッドがあります.
巡回路を生成した後,遺伝子配列に巡回路をコピーしています.
適合度計算
適合度はpower law scaling に基づいて計算されます.
都市数$n$ はMapクラスから,巡回路長$l$ はTourクラスのgetDistance()メソッドで取得できます.
\mathrm{Fitness} = \left(\frac{n}{l} \right)^3
再生・選択
プログラム中では,Individualsクラスを2つ使います.
parents で,遺伝子操作を行い.次世代で染色体の適合度に基づいてchildren にparents中の染色体を生き残らせます.
parentsには$N_{\mathrm{p}}$ 個,childrenには$N_{\mathrm{c}}$ が格納されています.(ただし,$N_{\mathrm{p}} \geq N_{\mathrm{c}}$)
生き残りに関しては,parents中の染色体を適応度の高い順に上位$N_{\mathrm{c}}$ 個の染色体を生き残らせます.ただし,エリート個体を必ず個体群の中に入れなければならないので,個体群中で最も適合度の高い染色体の適合度がエリート染色体の適合度より大きい場合,エリート個体を個体群中で最も適合度の高い染色体に更新します.そうでない場合は,$N_{\mathrm{c}}$番目の染色体をエリート染色体に置き換えます.
生き残った個体群children から遺伝子操作を行う親染色体を選択する方法は,children中の染色体$C_i$ の適合度が$f_i$ のとき,親個体で生き残る期待値を以下の式から計算します.
\mathrm{Experience} = \frac{N_{\mathrm{p}} \times f_i}{N_{\mathrm{c}} \times \overline{f}}
$\overline{f}$は children中にある染色体の適合度の平均値です.
期待値の数(小数点以下切り捨て)だけ,親染色体を選んでparentにコピーしていきます.小数点以下の部分は,ルーレット選択に使います.
すべて染色体に関して,期待値の数だけ親を選択すると,parentにはいくつか空の染色体が出てきます.残りの親はルーレット選択によって親を選択していきます.
選ばれた親の中から,同じ染色体が選ばれないようにするため,親染色体の中からかぶらないようにランダムに2つずつ選択して,それらを交叉します.
交叉・突然変異
交叉は交叉確率に基づいて行い,突然変異は突然変異確率に基づいて行います.
詳しいことは参考文献[2]をご覧ください.
遺伝子の矯正
遺伝的アルゴリズムは大域的最適解を求める力が強い反面,局所探索能力が弱い欠点があります.
なので,巡回セールスマン問題における逐次改善法の一つである2-opt 法による遺伝子の矯正を適合度の計算の前に行います.
実際に実行してみた
$N_{\mathrm{c}} = $100, $N_{\mathrm{p}} = $150,最大世代数:300,交叉確率:0.8,突然変異確率:0.1で52都市のベンチマーク問題Berlin52(最適値:7544.366)に適用しました..
完成した経路は同じディレクトリのresult.csv にデータが巡回路が出力されます.
city_num= 52
565.000 575.000
25.0000 185.000
345.000 750.000
(中略)
595.000 360.000
1340.00 725.000
1740.00 245.000
start...
0 7742.647
1 7742.647
2 7742.647
3 7742.647
4 7544.366
5 7544.366
6 7544.366
(中略)
294 7544.366
295 7544.366
296 7544.366
297 7544.366
298 7544.366
299 7544.366
300 7544.366
7544.366
stop.
処理時間:3157/ms
さいごに
この枝交換交叉は巡回スケジューリング問題を遺伝的アルゴリズムで解く方法において,枝組み立て交叉の手法の次くらいに良い手法だといわれています.
巡回セールスマン問題について遺伝的アルゴリズムを解く手法では,枝組み立て交叉を使った手法が現在,最も優れた手法だといわれています.いずれ,挑戦してみたいなと思っています.
スケジューリング問題についての研究しているので,スケジューリング問題で解くプログラムを作れればいいなと思ってます.
ソースコード
ソースコードを公開しています.
Javaをあまり使っていない研究室にいたんで,コードが汚いかもしれません...
(アドバイスなど気軽にどうぞ.)
https://github.com/SHIMADONBEY/GAwithTSP.git